Приблизительность моделей

Действительность отображается моделью грубо или приблизительно, поскольку м одель – это абстракция. Она по определению всегда является лишь относительным, приближенным подобием системы-оригинала и в информационном отношении принципиально беднее последней. Это ее фундаментальное свойство.

Несущественные свойства отбрасываются, и сложная исходная задача сводится к идеализированной задаче, поддающейся математическому анализу.

С подобной абстракцией очень часто приходится встречаться. Например, в механике, при описании некоторых процессов зачастую не учитывается сила трения, либо принимается, что все тела абсолютно твердые, жидкости не имеют вязкости и тому подобное. Все это идеализированные модели реально протекающих процессов. Они являются абстракциями и не существуют в реальной действительности.

Рассмотрим конкретный пример. Построим математическую модель движения груза под действием на него пружины с целью оценки параметров колебательного процесса (Рис8).

Пусть груз массой m колеблется на горизонтальной плоскости под действием пружины нулевой массы с жесткостью к. Предположим, что противодействующие силы (в частности, сила трения) пренебрежимо малы и нас интересуют характер и частота колебаний.

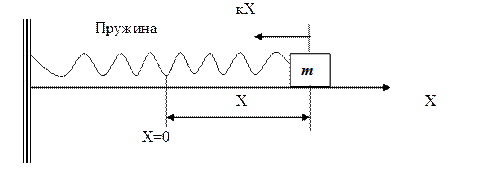
Рис.6. Схема колебательной системы

Для решения направим ось Х вдоль линии колебаний и выберем на ней начало отсчета, отвечающее равновесному положению груза, при котором пружина находится в нейтральном состоянии, т. е. ни сжата, ни растянута. Тогда, если положению груза соответствует координата Х, то на него действует сила -кХ. Применяя второй закон Ньютона (F=ma), получим дифференциальное уравнение

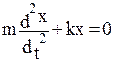(1)

с общим решением .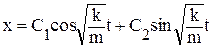

Здесь С1 и С2 –константы, определяемые из начальных условий. Таким образом, груз совершает гармонические колебания с центром в точке Х=0, с частотой

.

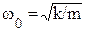Соответственно период колебаний равен

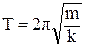
Это уравнение является математической моделью рассматриваемых свойств системы.

Но эта модель не точна. В действительности, в реальной системе колебания затухают. Однако ни каких сведений об этом мы получить из модели не можем. Модель не учитывает силу трения.

Дата добавления: 2014-12-16