Основные положения. Исследования операций (ИСО) – научная дисциплина, занимающаяся разработкой и практическим применением методов наиболее эффективного управления различными

Исследования операций (ИСО) – научная дисциплина, занимающаяся разработкой и практическим применением методов наиболее эффективного управления различными организационными системами. Под этим термином мы будем понимать применение математических, количественных методов для обоснования решений во всех областях целенаправленной деятельности человека.

(что мы исследуем) Операция – любое управляемое мероприятие, направленное на достижение цели.

(что такое решение) Решение это выбор из ряда возможностей, имеющихся у человека (лица, принимающего решение). Поясним. Пусть предпринимается какая-то операция, направленная на достижения определенной цели. У лица (или группы лиц), организующего операцию, всегда имеется какая-то свобода выбора: оно может организовать ее тем или другим способом, например, выбрать образцы техники, которые будут применены, так или иначе распределить имеющиеся средства и т. д.

Оптимальные решения – такое решение, которое по тем или иным соображениям предпочтительней других, поэтому основной задачей ИО является предварительное количественное обоснование оптимальных решений.

Исследование операций начинается тогда, когда для обоснования решений применяется тот или другой математический аппарат.

Примеры.

План снабжения предприятий. Имеется ряд предприятий, потребляющих известные виды сырья, и есть ряд сырьевых баз, которые могут поставлять это сырье предприятиям. Базы связаны с предприятиями какими-то путями сообщения со своими тарифами. Требуется разработать такой план снабжения предприятий сырьем (с какой базы, в каком количестве и какое сырье доставляется), чтобы потребности в сырье были обеспечены при минимальных расходах на перевозки.

Постройка участка магистрали. Сооружается участок железнодорожной магистрали. В нашем распоряжении определенное количество средств: людей, строительных машин, ре­монтных мастерских, грузовых автомобилей и т. д. Требуется спланировать строительство (т. е. назначить очередность работ, распределить машины и людей по участкам пути, обеспечить ремонтные работы) так, чтобы оно было завершено в минимально возможный срок.

Продажа сезонных товаров. Для реализации определенной массы сезонных товаров создается сеть временных торговых точек. Требуется выбрать разумным образом: число точек, их размещение, товарные запасы и количество персонала на каждой из них так, чтобы обеспечить максимальную экономическую эффективность распродажи.

Выборочный контроль продукции. Завод выпускает определенного вида изделия. Для обеспечения их высокого качества организуется система выборочного контроля. Требуется разумно организовать контроль (т. е. выбрать размер контрольной партии, набор тестов, правила браковки и т. д.) так, чтобы обеспечить заданный уровень качества при минимальных расходах на контроль.

Медицинское обследование. Известно, что в каком-то районе обнаружены случаи опасного заболевания. С целью выявления заболевших (или носителей инфекции) организуется медицинское обследование жителей района. На это выделены материальные средства, оборудование, медицинский персонал. Требуется разработать такой план обследования (число мед пунктов, их размещение, последовательность осмотров специ­алистами, виды анализов и т. д.), который позволит выявить по возможности максимальный процент заболевших и носителей инфекции.

Все эти задачи объединяет следующее: речь идет о каком-то мероприятии, преследующем определенную цель. Заданы некоторые условия, характеризующие обстановку (в частности, средства, которыми мы можем распоряжаться). В рамках этих условий требуется принять такое решение, чтобы задуманное мероприятие было в каком-то смысле оптимальным.

Оптимальными называется решение, по тем или другим признакам предпочти­тельное перед другими решениями.

Цель исследования операций — предварительное количественное обоснование оптимальных решений.

Чтобы сравнивать между собой по эффективности разные решения, нужно иметь какой-то количественный критерий, так называемый показатель эффективности. Его называют целевой функцией, обозначать будем так- W.

Если показатель эффективности желательно максимизировать (минимизировать), то будем записывать это так:

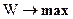
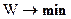
Например. План снабжения предприятий. Задача операции обеспечить снабжение сырьем при минимальных расходах на перевозки. Показатель эффективности W — суммарные расходы на перевозки сырья за единицу времени .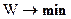

Показатель эффективности зависит только от двух групп параметров: от множества заданных условий – А и множества элементов решения – Х, то есть

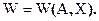
В числе условий А фигурируют и ограничения, налагаемые на элементы решения. Пусть решение Х представляет собой совокупность n элементов решения х,, х₂,..., х_п:

Требуется найти такие значения х₁, х₂,..., х_n, которые обращают величину W в максимум или в минимум (то есть найти «экстремум»). Это есть математическая интерпретация задач ИСО.

Дата добавления: 2014-12-16