Это и есть модель складских расходов

Задача управления запасами.

Чтобы процесс производства протекал непрерывно и независимо от поставок сырья необходимо, чтобы на месте производства был создан некоторый запас этого сырья. Тогда ставится вопрос: каков должен быть объем этих запасов?

В общем виде задача управления запасами относится к задачам нелинейного программирования и не имеют общих методов решения. Разработаны методы решения частных задач.

Постановка задачи. (однопродуктовая задача, с удорожанием продукции).

Имеется склад готовой продукции - изделий. Будем считать, что на складе хранится запас однотипных изделий, например, мешки с цементом. Спрос на эти изделия - равномерный и постоянный. Известен годовой спрос на эту продукцию (потребность на год).

Рис. 11 График годового спроса

Однако хранить годовой запас не выгодно – стоимость хранения велика. В связи с этим, на складе изначально хранится запас меньше годового спроса и он пополняется по мере расходования.

Пополняется склад при снижении запасов до некоторого уровня путем организации нового заказа. Объем заказа— это количество заказываемых изделий. Время выполнения этого заказа на пополнение склада (время поставки) будем считать постоянным. Каждый раз заказывается постоянное количество продукции. Известна стоимость подачи заказа (издержки на доставку – накладные расходы) и стоимость хранения одной единицы продукции.

Кроме того, в силу инфляции нереализованная продукция (хранящаяся на складе) постоянно дорожает. Будем считать, что удорожание продукции происходит равномерно и постоянно. Известен годовой процент удорожания.

Рис. 12 График удорожания продукции

Необходимо построить модель работы склада в течение года и оценить его издержки, определить оптимальный размер заказа с целью минимизации издержек. Если хранить большой запас, то мы выигрываем на издержках по доставке (количество доставок в год уменьшится) и на удорожании продукции, но много потеряем на хранении большого запаса. Нужна оптимизация. Издержки складываются из стоимости подачи заказов, стоимости хранения продукции и потерь в силу удорожания продукции.

Формальное описание постановки.

По содержательному описанию работы склада, который заключается в продаже со склада материалов и периодическом пополнении склада, мы можем построить следующий процесс обеспечения спроса в виде графика. График этот будет циклическим, поскольку запас на весь год делать нельзя, так как хранение большого объема продукции (в начале года) приведет к большим складским потерям. Делать маленький запас и часто его пополнять так же не выгодно, поскольку продукция дорожает и каждая поставка (пополнение) так же проводит к дополнительным затратам.

Рис. 13 График управления запасами

Введем обозначения:

D – годовой спрос продукции;

N - количество рабочих дней в году;

q – оптимальный размер заказа (неизвестная величина);

t – время доставки заказа;

C₀ – начальная стоимость единицы продукции;

k – годовой коэффициент удорожания единицы продукции;

C_s – издержки на однократное пополнение склада (не зависит от величины заказа);

C_h – издержки хранения единицы продукции в день;

Z – общие издержки организации склада (целевая функция);

Z₁ – общие издержки на пополнение склада;

Z₂ – общие издержки хранения продукции;

Z₃ – потери на удорожании продукции.

Тогда:

· Ежедневный расход продукции составляет D/N.

· Поскольку время доставки каждого заказа постоянно t, то уровень повторного заказа равен произведению ежедневного расхода на количество дней поставки заказа - t(D/N).

· Количество заказов, реализуемых за год равно годовому спросу, деленному на величину оптимального размера заказа D/q (количество циклов поставки).

· В течение одного цикла объем хранимой продукции равен q/2 (интеграл от линейной функции расхода), это и является средней величиной ежедневного хранения.

Построение математической модели.

Целевая функция - общие издержки равны Z = Z₁ + Z_{2 +} Z₃→min

Издержки пополнения склада равны стоимости всех заказов Z₁ = C_s(D/q).

Издержки хранения продукции равна средней хранимой величины на годовую стоимость хранения Z₂ = C_h (q/2).

Потери на удорожании продукции Z₃ = k C₀(D – q)/2.

Последнее выражение получено следующим образом.

· Одноразовая закупка на весь год

· Два цикла закупки

)

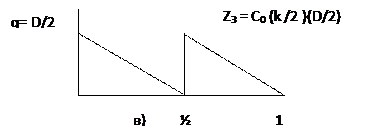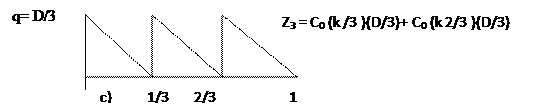· Три цикла закупки

Рис. 14. Графики удорожания

· n - циклов закупки Z₃ = C₀ (k /n)(D/n)+ C₀ (k 2/n)(D/n) + …+

+C₀ (k (n-1)/n)(D/n) = C₀ k D(2+3+…+n-1)/n²

Количество циклов n= D/q. Сумма прогрессии равна n(n-1)/2

Тогда Z₃ = k C₀(D – q) /2.

В итоге мы получили аналитическое выражение складских потерь

Z = C_s(D/q) + C_h (q/2) + k C₀(D – q) /2.

Исследования модели

Проведем минимизацию затрат по параметру объема закупки– q.

Найдем условие минимума функции (производную приравняем к нулю).

Z^`= - C₀ D(1/q) + C_h /2 - k C₀ /2 = 0

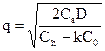, где k C₀- есть удорожание единицы продукции в год.

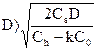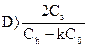Уравнение разрешимо, когда k C₀ < C_h удорожание меньше издержек хранения. Но, если у нас больше одной закупки в год, то D> q, тогда , или , или .

Дата добавления: 2014-12-16