Уравнение связи

Корреляция

В математической статистике связи между элементами системы, их свойствами и параметрами (а так же с внешней средой) изучаются методом корреляции.

Основная задача корреляции заключается в следующим. На основе большого количества статистических данных выявить, как изменяется в среднем зависимая переменная (выбранная в качестве характеристики системы) в связи с изменением какой либо независимой переменной. Это изменение предполагает условие неизменности других независимых переменных, хотя искажающее их влияние на самом деле имеет место.

Надо понимать, что небольшое число статистических данных не дает возможности обнаружить закономерность связи.

Наблюдая статистическую связь между зависимым и независимым переменными, математическая статистика стремится придать этой связи форму функциональной, то есть связи, выражаемой при помощи математической функции. Такая функция называется уравнением связи.

На помощь при отыскании уравнения связи приходит его графическое изображение. При этом необходимо стремиться найти такую функцию, которая давала бы наименьшее отклонение от имеющихся статистических данных и выражала бы основную зависимость в них.

Например, имеется некоторое множество точек наблюдений. Через них всегда можно попытаться провести такую прямую линию, которая является наилучшей в определенном смысле среди всех прямых линий, то есть «ближайшей» к точкам наблюдений по их совокупности.

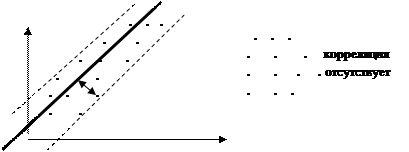у

х

Рис. 17 Близость прямой к совокупности точек.

Для этого нужно вначале определить понятие близости прямой к некоторому множеству точек на плоскости. Меры такой близости могут быть различными. Они, так или иначе, связаны с расстояниями от точек наблюдений до рассматриваемой прямой линии.

Графическое изображение изучаемых явлений позволяет не только установить на­личие или отсутствие связи между ними, но и изучить характер этой связи, иначе говоря, изучить форму связи.

Таблица8

Группы магазинов по числу рабочих мест	Число магазинов	Товарооборот на одного работника
	19 893
	18 030
3-4	16 508
5-7	8 321
8-10	2 868
11-15	1 559
16 и более	1 196

Возьмем, например, группировку магазинов по числу рабочих мест и будем откладывать число рабочих мест по горизонтальной оси (оси Ох), а товарооборот в расчете на одного работника — по вертикальной оси (оси Оу). Будем иметь ряд точек, соединив которые получим ломаную линию, которая называется ломаной регрессии.

135 ТО

0 1 2 4 6 10 12 16 Число раб. мест.

Рис. 18 Зависимость товарооборота магазина от числа рабочих мест

Как видно из графика, с ростом числа рабочих мест в магазине растет и товарооборот, приходящийся на одного работника, что говорит о связи между этими признаками, причем связи прямой. График подчеркивает эту зависимость ходом ломаной линии из нижнего угла в верхний правый угол.

Графическая модель наглядно иллюстрирует зависимость между элементами системы. Недостаток ее заключается в том, что она позволяет изобразить связь лишь между двумя элементами.

Дата добавления: 2014-12-16