Элементарные математические модели

Математические схемы случайностей

Сбор статистических данных при исследовании любых реальных систем (в физике, химии, биологии, медицине и др.) обладает тем свойством, что на них влияет огромное множество случайных факторов. Поэтому все статистические данные являются случайными. Закономерности, содержащиеся в них проявляются только в среднем.

В математической статистике рассматриваются следующие конструкции случайности.

· СЛУЧАЙНАЯ ВЕЛИЧИНА — величина, которая может принимать от случая к случаю то или иное свое значение. Задается законом распределения. Делятся на величины, распределенные дискретно и непрерывно. Дискретные случайные величины принимают каждая свое значение с определенной вероятностью, в то время как непрерывные случайные величины характеризуются плотностью вероятности. Многие их свойства описываются математическим ожиданием и дисперсией.

· СЛУЧАЙНОЕ СОБЫТИЕ — событие, которое может произойти, а может и не произойти. Наступление случайного события характеризуется вероятностью или плотностью вероятности. Вероятность случайного события характеризует частоту наступления случайного события, если указанные события повторяются большое количество раз.

· СЛУЧАЙНЫЙ ПРОЦЕСС — случайная величина, зависящая от времени. Закон распределения такой величины есть функция пространственных переменных и времени. Теория случайных процессов имеет многочисленные и важные приложения к физике, технике (броуновское движение, распространение радиосигналов при наличии помех и т. п.).

Каждая такая конструкция имеет свою математическую модель. Очень часто для сложных системы с большим числом случайных факторов строятся имитационные модели методом Монте-Карло.

Статистические данные (результат эксперимента, наблюдений, измерений) имеют случайную природу. И задача ставится так.

Пусть для определения значения некоторого параметра системы х (являющегося случайной величиной) произведено n независимых измерений. Эти измерения дали следующие значения параметра у₁, у₂,..., у_n, то есть

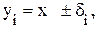
где δ_i – случайная ошибка i-го измерения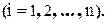

Какое значение y_i принять за значение неизвестного параметра, какова должна быть модель? Простейшими моделями случайной величины являются:

· Выборочное среднее (арифметическое) значение:

.

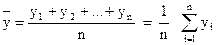· Функция распределения F(x) случайной величины x:

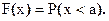
Функция F(x) есть неубывающая функция; 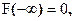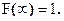Значение функции в некоторой точке а равно вероятности того, что случайная величина х примет значение, меньшее а.

В случае непрерывной случайной величины:

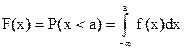, где f(х) – плотность распределения случайной величины х.

В случае дискретной случайной величины функция распределения есть сумма вероятностей всех случайных величин x_i меньших заданного а:

.

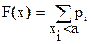Функция распределения может иметь различный вид. Наиболее часто встречающееся в практике: нормальное распределение (распределение Гаусса), равномерное, экспоненциальное.

Пример нормального распределения:

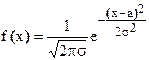
f(x) F(x)

x x

Рис. 16 Нормальное распределение

· Математическое ожидание дискретной случайной величины (имеющей дискретное распределение):

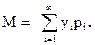, где p_i - вероятность того, что случайная величина х примет случайное значение y_i (i пробегает некоторое множество индексов).

В случае непрерывной случайной величины:

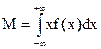, где f(х) – плотность распределения случайной величины х.

Следует иметь в виду, что при большой выборке экспериментальных данных работает закон больших чисел. Согласно этому закону, при большом числе опытов среднее арифметическое наблюдаемых значений случайной величины почти наверняка мало отличается от её математического ожидания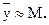

· Дисперсия случайной величины. Она отражает степень кучности случайной величины около своего математического ожидания. В случае дискретной случайной величины дисперсия равна:

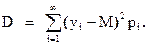
В случае непрерывной случайной величины дисперсия равна:

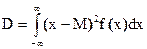, где f(х) - плотность распределения, М- математическое ожидание случайной величины.

Дата добавления: 2014-12-16