
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Дифференциальные уравнения. Двойной интеграл [1, гл.III]
|
|
|
|
Решение.
Тема 3
Двойной интеграл [1, гл.III]
Рассмотрим на нескольких примерах приемы вычисления двойных интегралов.
Пример 8. Вычислить повторный интеграл 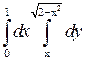 , затем изменить порядок интегрирования, вычислить полученный интеграл и сравнить ответы.
, затем изменить порядок интегрирования, вычислить полученный интеграл и сравнить ответы.
а) 
б) Строим область интегрирования (заштрихованная рис.1) согласно заданным пределам по x и по y и меняем порядок интегрирования.Эту область разобъем отрезком прямой y=1 (x 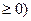 на две замкнутые области D
на две замкнутые области D  . В D
. В D 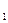 y изменяется от 0 до 1, а x изменяется от 0 до y. В D
y изменяется от 0 до 1, а x изменяется от 0 до y. В D  имеем 1
имеем 1  . Окончательно поучим:
. Окончательно поучим:

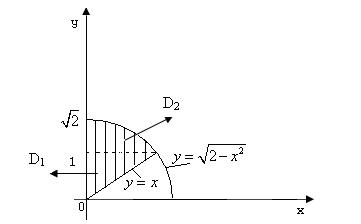
Рис.1
Пример 9. Вычислить двойной интеграл  по области
по области
 .
.
Решение. Представим двойной интеграл в виде повторного: сначала по х, затем по у (рис.2)
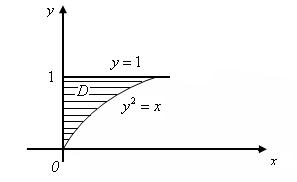
Рис. 2
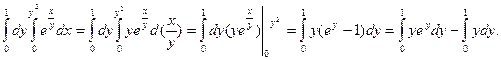
Интеграл 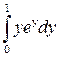 найдём по частям.
найдём по частям.
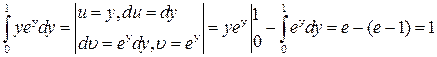
Интеграл  . Поэтому
. Поэтому  .
.
Тема 4 [4,гл.XIII]
Простейший пример дифференциального уравнения первого порядка первой степени, разрешенное относительно производной, имеет вид
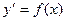 .
.
Функция f(x) предполагается непрерывной на некотором интервале (a,b) оси x. Пользуясь другим обозначением производной, можно записать это уравнение в виде

Множество решений этого уравнения даётся формулой
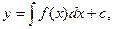 (1)
(1)
где с- произвольная постоянная.
Пример 10. Найти общее решение уравнения
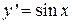 .
.
Решение. Согласно (1) имеем 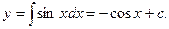
Уравнения вида
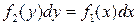 (2)
(2)
называются уравнениями с разделенными переменными. Функции  будем считать непрерывными.
будем считать непрерывными.
Пример 11. Найти общее решение дифференциального уравнения
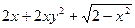 y′=0.
y′=0.
Решение. Перепишем его в виде
2x(1+y 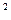 )+
)+ 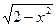
 =0.
=0.
Домножим обе части на dx≠0 и получим
2x(1+y 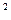 )dx+
)dx+ 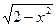 dy=0.
dy=0.
Это уравнение с разделяющимися переменными.
Левую и правую части полученного уравнения разделим на (1+y 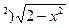 и проинтегрируем:
и проинтегрируем:
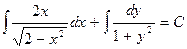 ,
,
arctgy-2 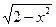 =C.
=C.
Пример 12. Найти общий интеграл уравнения
y′=  .
. 


Решение. Это уравнение является однородным, так как сводится к виду y′=f(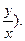
Разделим числитель и знаменатель исходной дроби на 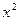 ≠0.
≠0.
Получим: y′= 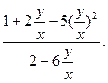 Замена
Замена 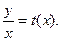
Тогда y=x·t(x) и y′=1+x·t′.
Следовательно
t+xt′= 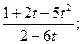
x·  .
.
Разделяем переменные x,t и интегрируем:

2arctgt-3ln(t 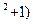 =ln
=ln  +c.
+c.
Возвращаясь к старым переменным y и x, получим
2 arctg 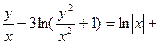 c.
c.
|
|
|
|
|
Дата добавления: 2014-12-16; Просмотров: 409; Нарушение авторских прав?; Мы поможем в написании вашей работы!