Теплопроводность. Уравнение теплопроводности в конечных разностях. Теплофизические характеристики строительных материалов. – 1 час 4 страница

Механическую вентиляцию в зданиях желательно разделять на зо­ны по фасадам, по высоте здания и, конечно, по назначению помеще­ний, что позволит осуществлять гибкое регулирование в течение года.

Может быть, два подхода к выбору принципиальных схем венти­ляции, учитывающих направленность инфильтрации. Можно исполь­зовать при вентиляции естественные процессы инфильтрации в ниж­них этажах и эксфильтрации в верхних или противодействовать им искусственной вентиляцией. В первом случае в нижней зоне зда­ния должна превалировать вентиляционная вытяжка, а в верхней — приточная вентиляция, работающая на выдавливание. Во втором-слу­чае вентиляцию используют для выравнивания фильтрационного режима здания по высоте. В нижней зоне создают подпор приточной вентиляцией, а в верхней обеспечивают интенсивную вентиляционную вытяжку. В обоих случаях необходимо заботиться о предупреж­дении перетекания воздуха из «загрязненных» помещений в чистые. Анализ режима вентиляции в связи с воздушным режимом здания необходим не только для зимнего периода, но также для переходного и летнего времени года.

В промышленных зданиях воздушный (аэрационный) режим опре­деляет распределение воздуха по помещениям и давление в них. От него в большой мере зависит режим работы воздушных завес у во­рот, местных отсосов, особенно с естественным побуждением, и других вентиляционных устройств. В лабораторных, больничных и других подобных зданиях расчет воздушного режима должен установить, прежде всего, возможные пути движения воздуха в здании, а венти­ляция должна предупредить перетекание загрязненного воздуха между смежными помещениями различного назначения.

Необходимый для данного здания воздушно-тепловой режим должен обеспечиваться наряду с разумной организацией отопления и вентиляции определенными конструктивными мерами и объемно-планировочными решениями.

Должна быть достаточная герметизация не только наружных ограждений, но и внутренних ограждений и проемов в них. Необ­ходимо устройство шлюзов, изолирующих здание от наружного воздуха и разделяющих его по высоте, незадымляемых лестничных клеток, изолированных от основного здания и сообщающихся по всей высоте с наружным воздухом. Необходимо учитывать дополнительные противопожарные меры и специальные требования незадымления путей эвакуации в здании.

Сложная задача определения оптимальной совокупности различ­ных отопительно-вентиляционных и конструктивно-планировоч­ных решений может быть решена методом сопоставления вариантов с помощью ЭВМ.

Лекция 8

Теплопроводность

Наружные ограждения должны предохранять помещения здания от непосредственных атмосферных воздействий. Эти функции огражде­ний оказываются достаточно важными в общей (с системами конди­ционирования микроклимата) задаче создания микроклимата поме­щений.

На внутреннюю поверхность наружного ограждения излучением и конвекцией передается определенное количество тепла. В холодный период года это тепло теряется через материальные слои ограждения в сторону внешней среды. Основное сопротивление потере тепла ока­зывают теплозащитные свойства материала ограждения. В стационар­ных условиях все тепло, воспринятое поверхностью ограждения в по­мещении, передается наружному воздуху. Такой режим характерен для зимних условий при небольших колебаниях температуры внутри и снаружи здания.

В летний период года ограждения должны защитить помещения от полуденного зноя, воспрепятствовать резкому колебанию температуры в нем под влиянием быстро изменяющихся в течение суток температуры наружного воздуха и солнечной радиации. В процессе нестационарной теплопередачи стены и перекрытия могут аккумулировать часть про­ходящего через них тепла и в результате тормозить и уменьшать охлаж­дение или перегрев помещений.

Аналогично рассмотренным тепловым свойствам, ограждающие конструкции выполняют функции защиты и регулирования воздушно­го и влажностного режимов помещений. Ограждения, как правило, обладают воздухопроницаемостью и сорбирующими свойствами. Через ограждения обычно происходит передача влаги и этот процесс не должен приводить к переувлажнению конструкций.

Значительное повышение влажности материала ограждения свя­зано с потерей их теплозащитных качеств и долговечности. Интенсив­ность передачи тепла через ограждение влияет на температуру ее внут­ренней поверхности, определяющей в свою очередь теплообмен в по­мещении и комфортность условий в помещении.

Основной составляющей процесса передачи тепла через огражде­ния является теплопроводность через материальные слои толщи ог­раждения.

Уравнение теплопроводности в конечных разностях

Процесс теплопроводности в материальных слоях конструкции подчиняется закону Фурье, уравнение которого в дифференциальной форме рассматривается в курсе теплопередачи. В строительной теплотехнике задачи теплопроводности часто решаются инженерными мето­дами, в которых используется конечно-разностная форма записи этого уравнения.

Вывод уравнения теплопроводности в конечных разностях удобно проследить на примере одномерного температурного поля при передаче тепла через однородную стенку (рис.10, а). Стенка разбивается на элементарные слои конечного размера ∆х; принимается, что равно­мерно распределенные тепловые свойства материала стены как бы со­средоточены в пределах каждого слоя. Таким путем переходят от поля материала конструкции с равномерно распределенными теплофизическими параметрами к тепловой цепочке с сосредоточенными харак­теристиками. Принято считать, что тепловая емкость каждого элемен­тарного слоя сосредоточена в его центре, а проводимость тепла материа­лом между слоями характеризуется сопротивлением теплопроводности между центрами слоев. Полученная тепловая цепочка (рис. 10, б) состоит из тепловых емкостей, соединенных между собой термически­ми сопротивлениями.

Рис.10 К выводу уравнения теплопроводности в конечных разностях.

Процесс нестационарной передачи в толще определяется двумя за­конами: проводимости и аккумуляции тепла.

Согласно закону про­водимости тепловой поток q пропорционален градиенту температуры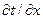

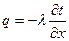(61)

где λ — коэффициент теплопроводности.

Знак минус показывает, что направление теплового потока про­тивоположно направлению температурного градиента (направлению возрастания температуры). Для участка стены между осями элемен­тарных слоев это уравнение можно написать в виде:

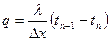(62)

где ∆x — расстояние между осями; t_n-1 и t_n — температуры на осях соседних элементарных слоев n — 1 и n.

В уравнении (62) принято, что температуры в центрах равны средним (интегральным) температурам по толщине элементарных слоев. Такое предположение строго справедливо только для линейного распределения температур в условиях стационарной передачи тепла.

Для нестационарных условий, учитывая криволинейное распределение температуры в слоях, уравнение (62) является приближен­ным.

При переходе к тепловой цепочке уравнение проводимости между ее узлами может быть записано в виде:

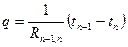(63)

где R_n-1,n =∆Χ/λ — сосредоточенное термическое сопротивление между узлами n-1 и n; t_n-1 и t_n — температуры в узлах тепловой цепоч­ки, где сосредоточены теплоемкости.

Уравнение (63) для тепловой цепочки справедливо как для ста­ционарных, так и нестационарных, в отличие от (62), условий.

Закон аккумуляции тепла устанавливает, что приращение коли­чества тепла dQ, аккумулированного слоем dx, пропорционально при­ращению во времени его температуры dt:

dQ = cρ dx dt, (64)

где сρ — объемная теплоемкость материала.

Изменение количества аккумулированного тепла ∆Q для элемен­тарного слоя толщиной ∆х при изменении во времени z его средней температуры на ∆_Zt равно:

∆Q = cρ ∆x ∆_Zt (65)

Для тепловой цепочки уравнение аккумуляции тепла может быть записано в виде:

∆Q = С∆_Zt (66)

где С=сρ∆х — сосредоточенная тепловая емкость элементарного слоя; ∆_Zt — изменение во времени (z) температуры в центре элемен­тарного слоя в сечении расположения сосредоточенной емкости.

Полная физико-математическая постановка задачи о нестационарной теплопередаче через многослойные ограждения

Одним из способов решения задачи нестационарной теплопередачи является аналитический метод. Этот метод позволяет получить наибо­лее общее решение, с помощью которого можно проанализировать все факторы, влияющие на изучаемое физическое явление. Однако ана­литически не удается решить многие сложные практические задачи, для которых приходится использовать инженерные методы. Для того чтобы воспользоваться аналитически­ми и приближенными методами, ин­женер должен, прежде всего, уметь правильно поставить задачу, математически сформулировать и записать ее условия.

Рис. 11 Схема ограждения - к рассмотрению полной физико-ма­тематической постановки задачи о нестационарной теплопередаче в многослойном ограждении.

Рассмотрим полную физико-мате­матическую постановку задачи неста­ционарной теплопередачи через мно­гослойное ограждение.

На рис.11 показана схема конструкции с обозна­чением слоев (1, 2, 3) и характерных границ, соответствующих внутренней І и внешней IV поверхностям ограж­дения и стыкам материальных слоев ІІ, ІІІ в его толще. Задача состоит в отыскании изменения температуры t(z, х) и тепловых потоков q(z, x) во времени z и в пространстве по толщине ограждения х.

Для решения любой задачи нестационарной теплопередачи должны быть заданы: а) начальные условия, определяющие распределение тем­пературы в толще и на границах ограждения в начальный момент времени; б) уравнения теплопроводности, описывающие процесс пере­дачи тепла через толщу конструкции; в) граничные условия, опреде­ляющие условия теплообмена на всех характерных поверхностях.

Начальные условия обычно задаются в виде уравнения (таблицы, графика) распределения температуры в момент начала процесса, т. е. при z = 0. В общем случае, оно записывается в виде:

t_нач =t (x, 0) (67)

Могут быть задачи без начальных условий, например при периоди­чески повторяющихся условиях теплообмена на границах.

Уравнения теплопроводности в толще ограждения могут быть записаны в двух вариантах.

Вариант А — нелинейное уравнение теплопроводности с перемен­ными коэффициентами:

(68)

где ср(х), λ(х) — заданные значения коэффициентов теплоемкости и теплопроводности отдельных материальных слоев в конструкции, ступенчато изменяющиеся от слоя к слою; в общем случае эти коэф­фициенты могут быть заданы изменяющимися по определенному зако­ну в пределах каждого слоя, переменными во времени, зависящими от температуры.

Вариант Б — система линейных дифференциальных уравнений с постоянными коэффициентами; каждое уравнение записано для от­дельного слоя с дополнительными условиями на границах - стыках ма­териальных слоев:

для слоя 1

для слоя 2 (69)

для слоя 3

От предполагаемого метода решения зависит целесообразность использования варианта А или Б для записи уравнений теплопровод­ности.

Граничные условия частично рассмотрены при записи основных уравнений по варианту Б. Кроме выражений этих уравнений должны быть записаны условия теплообмена на внутренней и наружной по­верхностях ограждения, соприкасающихся с внутренним t_в и наруж­ным t_H воздухом и окруженных другими поверхностями, имеющими температуру t_R.

Конвективный теплообмен определяется коэффициен­том а_к и лучистый — а_л. Нужно также учитывать, что ограждения могут облучаться сосредоточенными источниками тепла (солнца, на­гретая печь в помещении и др.). Количество поглощенного поверхно­стью лучистого тепла может быть определено так:

q_п = pq (70)

де р — коэффициент поглощения поверхности ограждения для дан­ного излучения; q — интенсивность падающего на ограж­дение излучения.

Теплофизические характеристики строительных материалов

Точность теплотехнического расчета при решении инженерной за­дачи в большой степени зависит от того, насколько правильно выбраны значения теплофизических характеристик строительных материалов конструкции. В расчетах теплопроводности используются два основ­ных показателя: теплопроводность λ, объемная теплоемкость сρ. В случае решения линейного уравнения, когда λ и сρ = const, удобно ввести коэффициент температуропроводности, который является про­изводным от λ и сρ и равным:

а = λ/(ср) (71)

Численные значения этих коэффициентов значительно изменяются в зависимости от состава, структуры и тепловлажностного состояния материалов.

Строительные материалы являются в своем большинстве сложны­ми капиллярно-пористыми телами, поры которых могут быть запол­нены влажным воздухом, жидкой влагой и льдом. Особенности строе­ния определяют большую изменчивость теплофизических характери­стик строительных материалов.

Теплопроводность λ, Вт/(м • К) [ккал/(м • ч • °С)], характеризует свойство материалов проводить тепло. В толще влажного строитель­ного материала передача тепла происходит несколькими путями. Через твердый скелет, а также пленки жидкой влаги и лед тепло передается посредством теплопроводности. В порах, заполненных влажным воз­духом, помимо теплопроводности теплообмен происходит конвекцией и излучением. При влагообмене тепло может переноситься жидкой и парообразной влагой, а также в результате фазовых превращений. Определенное количество тепла переносится фильтрующим через ма­териал воздухом.

Строительные материалы различаются между собой составом и строением их твердой части (скелета). Проводимость тепла скелетом материалов неорганического происхождения значительна выше, чем у органических материалов. Величины теплопроводности твердой час­ти неорганических материалов, Вт/(м • К) [ккал/(м • ч • °С)], равны: при аморфной структуре 0,7—3,5(0,6 — 3), при кристаллическом строе­нии 4,6—14 (4—12). Твердая часть материалов органического проис­хождения имеет λ=0,29—0,41(0,25—0,35), а пластмасс λ=0,16— 0,35 (0,14—0,3).

Материалы волокнистой структуры в большинстве случаев анизо­тропны и имеют значения теплопроводности при направлении тепло­вого потока вдоль волокон в два-три раза больше, чем при направлении потока поперек волокон.

Свойство теплопроводности при прочих равных условиях зависит от крупности пор. В сообщающихся порах могут возникать конвектив­ные токи воздуха, которые повышают проводимость тепла. Увеличе­ние пористости в таких материалах может привести к возрастанию общей теплопроводности.

Всю совокупность сложных явлений, участвующих в передаче теп­ла в толще материалов, обычно приводят к теплопроводности. Поэтому коэффициент теплопроводности строительного материала есть собира­тельный эквивалентный коэффициент, учитывающий все физические явления, происходящие в материале и связанные с передачей тепла.

Коэффициенты теплопроводности отдельных видов материалов за­висят от их объемной массы, влажности и температуры. В основном эти зависимости определяются соотношением составляющих, которы­ми может быть заполнен объем материала.

Теплопроводность λ, Вт/(м • К) [ккал/(м • ч • °С)], материала сильно отличается от λ воздуха, равного около 0,023 (0,02). Влага, заполняющая поры, имеет λ около 0,58(0,5), т. е. в 25 раз больше, чем у воздуха. При переходе в лед жидкой влаги теплопроводность ее уве­личивается вчетверо, так как λ льда около 2,3 (2,0). С увеличением объемной массы теплопроводность одного и того же материала заметно возрастает. Так, например, пенобетон при ρ = 400 кг/м³ имеет тепло­проводность 0,14 (0,12), при ρ = 600 она уже 0,21 (0,18), а при ρ = 1000, λ достигает величины 0,4 (0,34).

Важной для строительных материалов является зависимость λ от влажности. С увеличением влажности материалов коэффициент теплопроводности возрастает. Характер этой зависимости показан на рис. 7 на примере газосиликата и кирпича. Увеличение коэф­фициента связано с замещением воздуха в порах жидкой влагой, имею­щей более высокий коэффициент теплопроводности. На стыках между частицами материала пленки воды создают «водяные манжеты», ко­торые увеличивают площадь контакта между частицами и способствуют теплообмену между ними. Роль таких контактов особенно за­метна при небольших влажностях.

При высоких температурах λ с увеличением влажности растет быст­рее. Перенос тепла вследствие влагообмена оказывается тем больше, чем выше температура. При отрицательных температурах повышение влажности при прочих равных условиях также приводит к увели­чению λ.

При переходе в зону отрицательных температур не вся влага сразу превращается в лед. Сначала замерзает только свободная, связанная со скелетом материа­ла влага в крупных порах и ка­пиллярах. По мере понижения температуры количество твердой фазы влаги все более и более увеличивается за счет постепен­ного замерзания связанной вла­ги. Такой характер перехода жидкой влаги в лед в меньшей мере проявляется в чисто ка­пиллярно-пористых телах (пе­сок, обожженная керамика), где почти вся масса влаги замерза­ет уже при температуре—1, —3°С. Значительно сильнее этот эффект проявляется в коллоид­ных телах, таких, как глина. В некоторых видах глины, на­пример, меньше половины влаги замерзает при t = —20°С и даже при температурах — 70°С имеется заметное количество незамерзающей влаги.

Теплопроводность мерзлого материала, как правило, заметно вы­ше талого. Но при малых содержаниях льда в сравнительно крупных порах может образовываться рыхлый иней, в результате чего тепло­проводность не увеличивается, а уменьшается. Влажность материала в ограждениях изменяется во времени. В на­чальный период это связано с внесением в конструкцию «строительной влаги». В процессе эксплуатации (после того как часть влаги испарит­ся) материалы стен и перекрытий входят в некоторый установившийся квазистационарный равновесный влажностный режим. Влажность материала в этот период зависит от положения материала в конструк­ции, внутренних условий в помещениях здания и климата района по­стройки.

Значение λдля расчета теплового режима зданий принято устанав­ливать по так называемой «нормальной влажности» в период эксплуа­тации. В нормах даются три градации влажностного состояния конструкций, которые связаны с влажностными характеристиками внутреннего и наружного климата. Следует иметь в виду условность такого определения. Далее будут рассмотрены более полные рекомендации по учету влажностного режима.

Лекция 9

Дата добавления: 2014-12-16