Iv : Некоторые S и только S есть Р

Объединенная классификация простых суждений по коли- честву и качеству.

По логическому качеству суждения делятся на утвердительные и отрицательные. Утвердительность суждения грамматически никак не выражается, тогда как отрицательность выражается грамматической конструкцией “Неверно, что...”, обозначаемой на логических схемах символом Ø; например, “Неверно, что бегемоты летают” - Ø(S есть Р). В формальной логике используются следующие упрощающие предположения:

· если предмет не обладает каким-либо признаком, то неверно, что он обладает данным признаком:

(S не есть Р) ºØ(S есть Р); (22)

· если предмет не обладает каким-либо признаком, то он обла- дает признаком, противоречащим данному:

(S не есть Р) º(S есть Р); (23)

· если неверно, что предмет обладает каким-либо признаком, то он обладает признаком, противоречащим данному:

Ø(S есть Р) º(S есть Р). (24) По логическому количеству суждения подразделяются на общие, частные и единичные. В первом случае утверждается или отрицается, что все элементы определенного класса предметов обладают или не об- ладают некоторым свойством, находятся или не находятся в некотором отношении к другим предметам, существуют или не существуют.

Например, “Все рыбы дышат жабрами”, “Все родители старше своих детей”, “Все мифологические персонажи не существуют”. При- веденным выше суждениям соответствуют следующие логические схе- мы:

Все S есть Р или  х(S(x)ÉP(x)), (25)

 х(Q(x)ÉR(x, f(x))) (26)

(буквально: “Для всякого человека х верно, что если он родитель, то он старше своего ребенка”),

хØР(х) (27)

(буквально: “Для всякого х неверно, что он мифологический персо- наж”);

здесь  - квантор общности, а É- знак материальной импликации.

Частными называются суждения, посредством которых мы утвер- ждаем или отрицаем, что хотя бы один элемент определенного класса предметов обладает или не обладает некоторым свойством, находится или не находится в некотором отношении к другим предметам, суще- ствует или не существует. Например, “Некоторые люди не агрессивны”, “Некоторые птицы живут дольше людей”, “Некоторые легендарные герои существовали в действительности”. Данным су- ждениям соответствуют следующие логические схемы:

Некоторые S не есть Р или х(S(x) P(x)), (28)

хQ(x)y(P(y) R(x,y)) (29)

(буквально: “Существует х такой, что он птица, и существует у такой, что он человек, и х живет дольше у”);

x(Р(х) Q(x)) (30)

(буквально: “Существует х такой, что он легендарный герой и на- личествовал в действительности”).

Наконец, единичными называются суждения, соответствующие классу, включающему в себя один единственный предмет. Например, “Л.Н.Толстой - великий русский писатель”, “Каспаров играет в шах- маты лучше, чем Иванов”, “Бабы Яги нет”. В логике единичные су- ждения приравниваются к общим.

Сочетание классификационных признаков логического качества и логического количества позволяет построить объединенную классифи- кацию простых категорических суждений по количеству и каче- ству, которая включает в себя следующие четыре основных вида про- стых суждений:

·	общеутвердительное суждение (А) -
·	Все S есть Рили  х(S(x)ÉP(x)), общеотрицательное суждение (Е) -	(31)

Все S не есть Р или  х(S(x)ÉØP(x)), (32)

· частноутвердительное суждение (I) -

Некоторые S есть Р или х(S(x) P(x)), (33)

· частноотрицательное суждение (О) -

Некоторые S не есть Р или х(S(x) P(x)). (34) Если субъект и предикат атрибутивного суждения рассматривать как особые понятия, то простые атрибутивные суждения можно интер- претировать как специальные логические структуры, посредством ко- торых мы можем зафиксировать отношение объемов данных понятий. В том случае, если объем какого-либо термина суждения полностью входит или полностью не входит в объем другого термина, термин считается распределенным; если же объем какого-либо термина сужде- ния частично входит или частично не входит в объем другого тер-

мина, термин считается не распределенным.

О характере распределенности терминов в простых суждениях поз- воляют сделать вывод следующие объемные диаграммы:

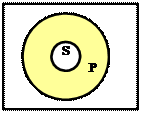
1. А: Все S есть Р.

S - распределено (+)

Р - не распределено () (35)

Исключение: общеутвердительное выделяющее суждение -

Аv: Все S и только S есть Р.

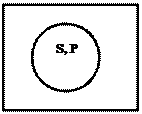S - распределено (+)

Р - распределено (+) (36)

Примечание. Данное суждение не является простым; это конъюнк- ция двух простых суждений -

А1А2,

гдеА1:Все S есть Р, А2: ВсеР есть S.

2. Е: Все S не есть Р.

или

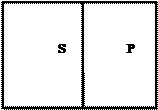(37)

или

S - распределено (+) Р - распределено (+)

3. I: Некоторые S есть Р.

или

(38)

S - не распределено () Р - не распределено ()

Исключение: частноутвердительное выделяющее суждение -

S - не распределено ()

Р - распределено (+) (39)

Примечание. Данное суждение не является простым; это - конъюнк- ция двух простых суждений -

гдеI1: Некоторые S есть Р, А1: ВсеР есть S.

4. О: Некоторые S не есть Р.

I1 A1,

или

(40)

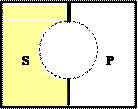или

S - не распределено () Р - распределено (+)

Общее представление о характере распределенности терминов в су- ждениях задается при помощи следующей таблицы:

Виды суждений   Термины	A	E	I	O
S	+	+	-	-
P	-	+	-	+

Дата добавления: 2014-12-16