
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Гармонические колебания
|
|
|
|
II. Основные законы теории колебаний и волн.
Гармонические колебания – колебания, происходящие по гармоническому закону (закону синуса или косинуса).
Х = А sin (ωt + φ0). (1)
В уравнении 1: А - амплитуда колебаний; (ωt + φ0) – фаза колебаний;
φ0- начальная фаза; ω – круговая (циклическая) частота.


вектора  , фаза – угол между вектором
, фаза – угол между вектором  и осью Х.
и осью Х.
Рассмотрим колебания горизонтального пружинного маятника. Один
|
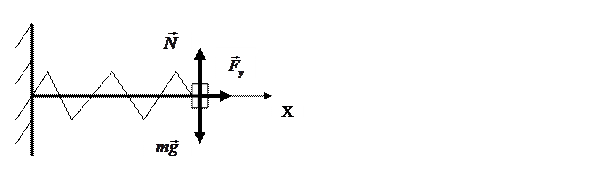
Запишем это уравнение в проекции на ось Х: ma=Fу или m(d2x/dt2)= -kx
Разделим обе части уравнения на m и перенесем все слагаемые в левую часть уравнения (d2x/dt2 )+ (k/m)x=0. Введем обозначения (k/m)=ω02, где ω0 - циклическая частота собственных колебаний. Перепишем уравнение
(d2x/dt2 ) + ω02 x=0 (2)
Получили уравнение второго порядка гармонических колебаний, так как
решением его является уравнение гармонических колебаний
Х=Аcos(ω0t + φ0)
Если подставить в уравнение 2 значения d2x/dt2 (d2x/dt2 =-А ω02 cos(ω0t + φ0)) и X (Х=Аcos(ω0t + φ0)), то получим -А ω02 cos(ω0t+φ0) +А ω02 cos(ω0t+φ0)=0.
Следовательно Х=Аcos(ω0t + φ0) является решением уравнения 2.
Круговая частота ω связана с частотой колебаний υ соотношением υ= ω/2π. Период колебаний Т=1/υ =2π/ω. Для пружинного маятника Т=2π 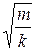 , для математического T =2π
, для математического T =2π 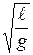 , для физического маятника
, для физического маятника 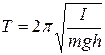 (I - момент инерции тела относительно оси, m –масса маятника, h – расстояние между центром тяжести и осью вращения).
(I - момент инерции тела относительно оси, m –масса маятника, h – расстояние между центром тяжести и осью вращения).
Скорость материальной точки колеблющейся по гармоническому закону: ν = dx/dt= - Aωsin(ωt + φ0) (3); ν = - νmax sin(ωt + φ0)=
νmax cos((ωt + φ0)+π/2), где νmax= Aω.
Фаза скорости больше фазы смещения на π/2.
Ускорение а = dν/dx =- Aω2 cos(ωt + φ0) (3);
a = - amax cos(ωt + φ0) =amax cos((ωt + φ0) + π) (4), где amax = Aω2.
Ускорение и смещение находятся в противофазе.
Кинетическая энергия колеблющейся материальной точки
Ек = (½)mν2 =(½)m A 2ω 2sin 2(ωt + φ0)
Ек =(½)k A 2sin 2(ωt + φ0) (5), где mω 2=k.
Потенциальная энергия
Еп =(½)к х2 =(½)к А 2cos 2(ωt + φ0) (5)
Полная механическая энергия
Е= Ек+ Еп=(½)k A 2 (sin 2(ωt + φ0)+ cos 2(ωt + φ0)) =(½)k A 2 (6)
При отсутствии сил трения полная механическая энергия сохраняется.
|
|
|
|
|
Дата добавления: 2014-12-16; Просмотров: 810; Нарушение авторских прав?; Мы поможем в написании вашей работы!
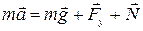 (1)
(1)