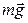Затухающие колебания

Действие сил трения существенно изменяет характер движения, колебание становится затухающим. Рассмотрим колебания горизонтального пружинного маятника.

На тело действуют сила тяжести 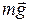сила упругости пружины 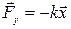, сила трения 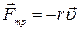, нормальная реакция опоры 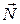. Запишем 2-й закон Ньютона.

= + + + .

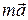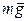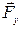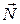Запишем это уравнение в проекции на ось Х:

ma=F_у+Fтр или m(d²x/dt²)= -kx – r(dx/dt).

Разделим обе части уравнения на m и перенесем все слагаемые в левую часть уравнения

(d²x/dt² )+ (r/m) (dx/dt) +(k/m)x=0.

Введем обозначения (r/m)=2β и (k/m)=ω₀², где β - коэффициент затухания, а ω₀ - циклическая частота собственных колебаний. Перепишем уравнение

(d²x/dt² )+ 2β(dx/dt) + ω₀² x = 0 (7)

Получили уравнение второго порядка затухающих колебаний. Решение этого уравнения существенно зависит от знака разности ω²= ω₀² – β², где ω циклическая частота затухающих колебаний.

При ω₀² – β²>O решение записывается в следующем виде:

X=A₀e^-βt cos(ωt +φ₀) (8), где

(A₀e^-βt) - амплитуда затухающих колебаний, которая изменяется по экспоненциальному закону.

Период затухающих колебаний Т=2π/ω= .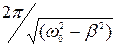

При очень малом трении (ω₀² >> β²) Т=2π/ω₀.

Быстрота убывания амплитуды колебаний определяется коэффициентом затухания β: чем больше β, тем сильнее торможение.

На практике степень затухания характеризуют логарифмическим декрементом затухания

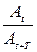λ =ℓn =ℓn 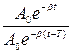= ℓn e ^βt= βt

λ= βt (9)

При сильном затухании (β²>ω₀²) период является мнимой величиной, а колебания апериодическими.

3. Вынужденные колебания. Резонанс. Автоколебания.

Вынужденными называют колебания, которые возникают в системе при участии внешних сил, изменяющихся по периодическому закону.

Пусть на горизонтальный пружинный маятник помимо указанных выше сил действует вынуждающая сила, изменяющаяся по закону

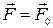cos ωt. Тогда по второму закону Ньютона:

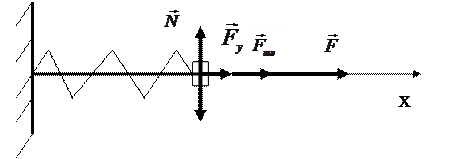
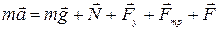
В проекции на ось Х ma = F_у+F_тр+F или m(d²x/dt²)= -kx – r(dx/dt) + F₀ cos ωt. Разделим на m и введем обозначения f₀=F₀/m, 2β=r/m; ω₀² =k/m.

Получаем: (d²x/dt²) +(r/m)(dx/dt) +(k/m)x = f₀ cos ωt.

(d²x/dt² )+ 2β(dx/dt) + ω₀² x= f₀ cos ωt. (10)

Решением этого уравнения является сумма 2-х слагаемых. Одно из них X=A₀e^-βtcos(ωt +φ₀). Это уравнение затухающих колебаний играет роль только при установлении колебаний. Со временем им можно пренебречь.

Другое слагаемое X=A cos(ωt +φ₀) (11) описывает смещение материальной точки в установившихся вынужденных колебаниях.

А= f₀/ 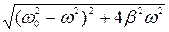(12); tg φ₀=-2βω/(ω ² – ω₀²)(13).

Как видно, вынужденное колебание так же является гармоническим. Частота его равна частоте вынуждающей силы. Амплитуда вынужденных колебаний прямо пропорциональна амплитуде вынуждающей силы и имеет сложную зависимость от коэффициента затухания β, а так же ω и ω₀.

Если знаменатель имеет минимальное значение, то амплитуда А имеет максимальное. Это явление резонанса. Резонансная частота 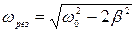(14), амплитуда А_рез=f₀/2β 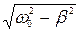(15). При отсутствии сопротивления (β≈0) А_рез→ ∞ и ω_рез→ω₀

Существуют колебательные системы, которые сами регулируют периодическое восполнение затраченной энергии. Незатухающие колебания, существующие в таких системах, называются автоколебаниями. Амплитуда и частота автоколебаний зависит от свойств самой системы. Примеры: в технике часы, генераторы электромагнитных колебаний; в биологии – сердце, легкие и т. д..

Дата добавления: 2014-12-16