Решение. В соответствии с уравнением (10), вытекающим из первого следствия из закона Гесса получаем:

Решение.

В соответствии с уравнением (10), вытекающим из первого следствия из закона Гесса получаем:

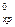ΔН = ΔН 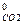+ 4 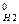ΔН - ΔН 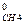- 2 ΔН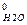

Подставляем значения стандартных величин образования (в кДж/моль) из справочных данных (табл,1 Приложения) и получаем

ΔН 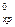= 1·(-393,51) + 4·0 – 1·(-74,85) – 2 ·(241,82)

Как видно, данная реакция является эндотермической.

Пример 2. Рассчитать стандартную энергию образования пропана С₃Н₈, если изменение стандартной энтальпии реакции его сгорания

С₃Н₈ + 5О₂ = 3СО₂ + 4Н₂О_(г)

равно ΔН 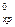= -2043,86 кДж/моль.

В соответствии с уравнением (10):

ΔН 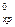= 3 ΔН 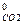+ 4 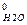ΔН – ΔН 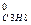– 5 ΔН ,

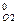откуда

ΔН 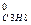= – ΔН 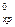+ 3 ΔН 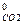+ 4 ΔН 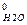– 5 ΔН ,

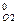Подставив значение ΔН 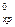и справочные данные из табл. 1 Приложения, получим:

ΔН 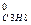= –(–2043,86) + 3(–393,51) + 4(–241,82) –5∙0 = -103,85 кДж/моль.

Как видно, реакция образования пропана относится к экзотермическим реакциям.

В общем случае тепловой эффект химического процесса зависит от температуры и давления, при которых осуществляется химическое превращение. Влиянием давления на ΔU и ΔН реакции обычно пренебрегают.

Теплоёмкостью с называют количество теплоты, необходимое для нагревания 1г (удельная теплоёмкость) или 1 моля (молярная теплоёмкость) вещества на 1 К.

с = 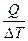. (12)

С повышением температуры теплоёмкость твёрдых, жидких и газообразных веществ увеличивается.

Различают истинную теплоёмкость, т.е. при теплоёмкость при данной температуре

с = 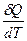(13)

и среднюю теплоёмкость

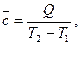(14)

которая соответствует конечному интервалу температур. При незначительной величине интервала теплоёмкость считают не зависящей от температуры.

В зависимости от условий нагревания теплоёмкость бывает изобарной с_р и изохорной с_v:

с_{р = 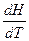,} (15)

с_{v = 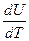.} (16)

Для выведения зависимости теплового эффекта от температуры продифференцируем уравнение (6):

Q_p = ΔН = H₂ – H₁,

учитывая уравнение (14), получаем:

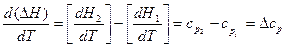. (17)

Уравнение (17) называют уравнением Кирхгофа, где Δс_р – это разность молярных теплоёмкостей продуктов реакции и исходных веществ с учётом стехиометрических коэффициентов.

Для вычисления теплового эффекта при заданной температуре Т, необходимо проинтегрировать уравнение Кирхгофа:

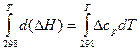, (18)

ΔН_Т = ΔН 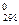+ 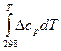. (19)

В широком диапазоне температур зависимость теплоёмкости веществ от температуры выражается в виде эмпирических уравнений:

с_р = a + bT + 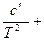c·T². (20)

Коэффициенты a, b, c, c' для продуктов реакции и исходных веществ приводятся в справочниках, далее вычисляют Δ a, Δ b, Δ c, Δ c' как суммы соответствующих величин для продуктов реакции, умноженные на стехиометрические коэффициенты минус соответствующие значения для исходных веществ. Затем зависимость

Δ с_р = Δ a + Δ bT + 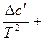Δc·T² (21)

подставляются под знак интеграла в уравнение (19) и производится расчёт ΔН_Т по правилам интегрирования.

При использовании табличных значений средних теплоемкостей 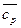величина Δ 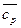является постоянной и может быть вынесена из-под знака интеграла:

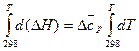, (22)

ΔН_Т = ΔН 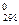+ 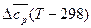. (23)

Для процессов, протекающих при постоянном объёме, соответственно, зависимость теплового эффекта от температуры описывается уравнением:

ΔU_T = 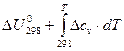. (24)

Пример 3. Определить теплоту, поглощённую при нагревании 100 г двуокиси углерода от 15 до 1000ºС при постоянном объёме, если

с 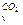= 27,24 + 0,00809t Дж/моль·град.

Решение. Объёмная теплоёмкость равна количеству теплоты, которое необходимо для нагревания на 1ºС 1м³ газа, приведённого к нормальным условиям. При повышении температуры от Т₁ до Т₂ количество поглощаемой теплоты можно рассчитать по формуле:

Q = 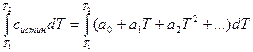(для 1 моля вещества)

После интегрирования выражение примет вид:

Q=[a₀ (T₂ – T₁) + a₁ ]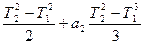

При вычислении по данной формуле температуру можно брать в градусах Цельсия.

Число молей углекислого газа определяем по формуле

ν =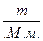

и тогда количество поглощённой теплоты в рассматриваемом процессе будет равно

Q =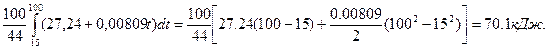

Дата добавления: 2014-12-16