Об'єднання множин. Властивості обєднання

об'єднання множин є множиною, яка включає в себе всі елементи об'єднуваних множин і нічого більше.

Якщо A та B — множини, то об'єднанням A та B є множина, яка включає всі елементи A і всі елементи B, і більш нічого.

Об'єднання множин A та B позначається як «A ∪ B».

Формально: x є елементом A ∪ B тоді й тільки тоді, коли

· x є елементом A або

· x є елементом B.

Наприклад, об'єднанням множин {1, 2, 3} та {2, 3, 4} буде {1, 2, 3, 4}.

Бінарна операція об'єднання є:

асоціативною, тобто A ∪(B ∪ C) = (A ∪ B)∪ C (отже, коли в виразі є тільки операція об'єднання, дужки можна не писати: A ∪ B ∪ C);

комутативною, тобто A ∪ B = B ∪ A (отже, порядок запису множин в виразі не має значення).

Порожня множина є нейтральним елементом для операції об'єднання в алгебрі множин. Тобто, Ø∪ A = A, для будь-якої множини A.

ідемподентною, тобто A ∪ A = A.

В загальному випадку, якщо M — множина, елементами якої є також множини, то x є елементом M тоді й тільки тоді, якщо існує такий елемент A з M, що x є елементом A. В символічній формі:

Позначення об'єднання довільної кількості множин такі:

або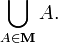

Остання нотація може бути узагальнена до

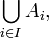
що відповідає операції об'єднання колекції множин { A_i: i в I }. Тут I — множина, а A_i — множина для кожного i в I.

В цьому випадку I є множиною індексів (натуральних чисел), і нотація є аналогічною узагальненій операції сумування:

Також можна записати «A ₁ ∪ A ₂ ∪ A ₃ ∪ ···».

Дата добавления: 2014-12-16