Нерівність зоднією змінною. Область визначення нерівності. Розв’язок нерівностей. Приклади

Поняття висловлення в математичній логіці. Види висловлень

Діаграма відповідності

Логіка – наука про форми і закони математичного мислення.

Основне поняття математичної логіки є висловлення.

Висловлення – в мат. Логіці розглядається, як велична, яка може мати два значення: і істинне(1) і хибне(0).

Висловлення, з яких не можна виділити коротші, простіші висловлення, називаються елементарними і позначаються маленькими латинськими літерами: a. b, c..

У розмовній мові використовуються сполучники: «і», «або», «якщо», «то»,» тоді і тільки тоді, коли», «не». Їм відповідають логічні операції, які позн. спеціальними знаками:

· кон'юнкції Λ (і)

· диз'юнкції V (або)

· імплікації →(якщо, то)

· еквівалентності =(тоді і тільки тоді, коли)

· заперечення (не)

Запереченням висловлення А назив. висловлення не А, яке істинне тоді і тільки тоді, коли А хибне.

Кон’юнкцією висловлень А, В назив. Складне висловлення, яке істинне, тоді і тільки тоді, коли істинні, обидва данні висловлення.

Диз’юнкцією А, В назив. Складне висловлення, яке хибне тоді тільки тоді, коли обидва дані висловлення хибні.

Висловлення «А то В», яке хибне тоді і тільки тоді, коли А істинне, В хибне, називається імплікацією.

Еквіваленцією двох висловлень А та В назив. Складне висловлення «А, тоді і тільки тоді, коли В», яке істинне тоді і тільки тоді, коли обидва висловлювання хибні, чи обидва істинні.

Нерівністю з однією змінною називається нерівність, що містить одну незалежну змінну. Розв’язком нерівності називається будь-яке значення змінної, при якому початкова нерівність зі змінною обертається у правильну числову нерівність. Розв’язати нерівність зі змінною – значить знайти всі її розв’язки або довести, що розв’язків немає. Дві нерівності називаються рівносильними (еквівалентними), якщо розв’язки цих нерівностей збігаються; зокрема, нерівності рівносильні, якщо вони не мають розв’язків.

Основні теореми про рівносильні нерівності.

1. Якщо з однієї частини нерівності перенести до іншої доданок із протилежним знаком, то дістанемо нерівність, рівносильну початковій.

2. Якщо до обох частин нерівності додати (або відняти) будь-яке число, то дістанемо нерівність, рівносильну початковій.

3. Якщо обидві частини нерівності помножити (поділити) на додатне число, то дістанемо нерівність, рівносильну початковій; якщо обидві частини нерівності помножити (поділити) на від’ємне число, то рівносильною початковій буде нерівність протилежного змісту.

Множина Х на якій визначена функція(існує дана залежність) називають областю визначення F.

Приклад:

Знайти область визначення і множину значень функцій:

а) 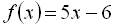; б) .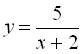

Розв’язання

а) 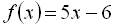. Оскільки область зміни х не вказано, природно областю визначення функції вважати множину всіх значень змінної х, при яких ця відповідність має сенс. Отже, у даному випадку .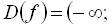

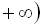Легко збагнути, що 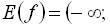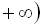. Знайдемо значення функції при декількох значеннях аргументу: , ,

.

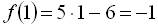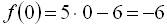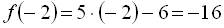Дата добавления: 2014-12-16