Теореми про рівносильність рівнянь

Означення: два рівняння f1(х)=g1(х) і f2(x)=g2(x) називаються рівносильними, якщо вони задані на одній множині та множини їх розв’язків співпадають.

Означення: два рівняння називаються рівносильними, якщо вони задані на одній множині та якщо кожен розв’язок першого рівняння є розв’язком другого рівняння і, навпаки, кожен розв’язок другого рівняння є розв’язком першого рівняння.

Означення: Якщо множина розв’язків рівняння 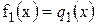є підмножиною множини розв’язків рівняння 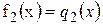, то рівняння 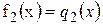називають наслідком рівняння .

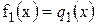Іншими словами, 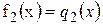- є наслідком рівняння 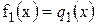, якщо кожний корінь рівняння 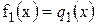задовольняє рівняння 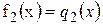. Наприклад, рівняння 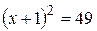є наслідком рівняння 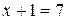, бо кожний корінь рівняння 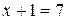є коренем рівняння 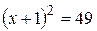. Отже, ми можемо дати ще одне означення рівносильних рівнянь.

Означення: два рівняння називаються рівносильними, тоді і тільки тоді, коли кожне із них є наслідком іншого.

Рівняння, множини розв’язків яких порожні, також прийнято вважати рівносильними. Якщо згадати, що рівняння є предикатами, то два рівняння будуть рівносильними, якщо предикати f1(х)=g1(х) і f2(x)=g2(x) еквівалентні. Для того, щоб з’ясувати, чи рівносильні рівняння, слід перевірити виконання умов наведених означень рівносильних рівнянь. Покажемо, як це робити на прикладі наступної вправи.

Теорема 1: Якщо вираз φ(х) визначений для всіх х є Х, то рівняння f(х)=g(х) (І) і f(х)+φ(х)=g(х)+φ(х) (ІІ) рівносильні.

Наслідок 1: будь-яке рівняння виду f(х)=g(х) рівносильне рівнянню виду F(x)=0.

Наслідок 2: будь-який член рівняння можна переносити із однієї частини рівняння в другу, міняючи при цьому його знак на протилежний.

Теорема 2: Якщо вираз φ(х) визначений і не перетворюється в нуль для всіх хєХ, то рівняння f(х)=g(х) (І) і f(х)●φ(х)=g(х)●φ(х) (ІІІ) рівносильні.

Дата добавления: 2014-12-16