Поняття множини. Елемент множини. Порожня множина. Способи завдання множини. Рівні множини. Підмножина. Види підмножин. Відношення рівності та включення множин

Множина́ — одне з основних понять сучасної математики. Строго воно не визначається, але може бути дано інтуїтивне визначення множини як сукупності певних і різних об'єктів довільної природи, яка розглядається як одне ціле. Об'єкти, які складають множину, називаються її елементами. Наприклад, можна говорити про множину усіх книг в певній бібліотеці, множину літер українського алфавіту або про множину всіх коренів певного рівняння тощо.

Об’єкти, з яких складається множина, є елементами множини. Множина однозначно визначається її елементами.

Порожня множина в математиці — множина, яка не містить жодного елемента. Така множина позначається як Ø або {}.

· Задання множини за допомогою переліку її елементів.

Нехай множина X складається з елементів a, b, c,..., k. Для означення цього факту використовується позначення:

X = {a, b, c,..., k}

A = {4, 2, 1, 3}

B = {червоний, білий, блактиний}

Наприклад, множина натуральних чисел ℕ визначається як:

ℕ = {1, 2, 3,..., n,...}

· Задання множини вказівкою властивості її елементів.

В математичних задачах, як правило, розглядають елементи деякої цілком означеної множини A. При цьому необхідні елементи виділяють за деякою їх властивістю (або вказують породжуючу процедуру) P, такою що кожний елемент x ∈ A або має властивість P (записується P(x)), або не має її. За допомогою властивості P виділимо множину всіх тих елементів, які мають властивість P. Цю множину будемо позначати як { x ∈ A | P(x) } = { x | P(x) }. Задання множини вказівкою її властивості (або породжуючим предикатом) слід здійснювати обережно. Наприклад, множина Y = {X|X∉X} (множина всіх множин, які не містять себе в якості елемента) веде допарадокса Рассела і є некоректною в аксіоматичній теорії множин.

Дві множини називаються рівними, якщо кожний елемент першої множини є елементом другої множини і, навпаки, кожний елемент другої множини є елементом першої множини. З наведеного означення рівності множин випливає, що в множині однакові елементи не розрізняються.

Якщо X та Y — множини та будь-який елемент із X є також елементом із Y, то говорять, що:

· X є підмножиною (частиною) Y, позначення — X ⊆ Y;

· Y — надмножина (охоплююча множина) X, позначення — Y ⊇ X.
Кожна множина Y є підмножиною себе самої. Підмножина Y, яка не збігається з Y називається точною підмножиною (або правильною чи власною частиною множини) Y. Якщо X — точна підмножина Y, то цей факт записується як X ⊂ Y. Відношення «бути підмножиною» має назву включення.

· Із означення прямо слідує, що порожня множина мусить бути підмножиною будь-якої множини. Також, очевидно, будь-яка множина є своєю підножиною:

· .

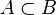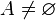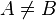· Якщо , і , , то 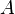називається власною або нетривіа́льною підмножиною.

Дата добавления: 2014-12-16