Рівняння з однією змінною. Овласть визначення рівняння. Розв’язок рівняння. Приклад

Нехай на множині М задано два вирази f(х) і q(x) з однією змінною х. Предикат виду f(х) = q(x), х Î М, для якого потрібно знайти область істинності, називається рівнянням з однією змінною. Вирази f(х) і q(x) називаються частинами рівняння, f(х) – лівою, q(x) – правою. У тому разі, коли хоч одна з частин рівняння є алгебраїчною сумою, доданки суми називаються членами рівняння. Множина М називається областю визначення рівняння

Залежно від області визначення рівняння може мати різні множини розв’язків. Наприклад, рівняння

(x – 1) (х + 2) (х2 – 3)(x2 + 1) = 0

на множині натуральних чисел має один розв’язок, бо тільки при х = 1 добуток множників дорівнює нулю, на множині цілих чисел – два розв’язки {–2; 1}, а на множині дійсних чисел – чотири розв’язки {–2; –; 1; }.

8. число елементів об єднання двох скінченних множин і доповнення до підмножин.

При розв'язуванні деяких задач потрібно вміти знаходити число елементів у об'єднанні кількох скінченних множин.

Знайдемо спочатку число елементів в об'єднанні двох довільних скінченних множин X і Y. Позначимо число елементів у множинах X, Y, X  Y і X  Y відповідно |X|, |Y|, |X  Y| і |X  Y|. У сумі |X| + |Y| спільні елементи множин X і Y, тобто елементи, що належать X  Y, враховуються двічі, а в |X  Y|, у силу того, що елементи не повторюються у множині, вони враховуються один раз, а тому матиме місце рівність

|X  Y| = |X| + |Y| – |X  Y|.

Рівність можна одержати також, скориставшись кругами Ейлера і вважаючи, що число елементів у множині є площею фігури, якою зображено дані множини (мал. 13).

Мал. 13.

Одержуємо теорему про число елементів в об'єднанні двох скінченних множин.

Теорема 2. Для довільних скінченних множин X і Y має місце рівність

|X  Y| = |X| + |Y| – |X  Y|.

Коли множини X і Y не перетинаються, тобто X  Y = , то з теореми 2 одержується наслідок.

Наслідок 1. Якщо множини X і Y – скінченні і не перетинаються, то має місце рівність

|X  Y| = |X| + |Y|.

Для довільних множин X і Y, коли множина Y є підмножиною множини X, тобто Y  X, то мають місце рівності

(X \ Y)  Y = X і (X \ Y)  Y = .

Звідси за наслідком 1 одержуємо, що для довільних скінченних множин X i Y, якщо Y  X, то має місце рівність

|X \ Y| + |Y| = |X|.

А тому, враховуючи одержану рівність та означення доповнення підмножини до множини, дістанемо теорему про число елементів у доповненні підмножини до множини.

Теорема 3. Для довільних скінченних множин X і Y, якщо Y  X, то має місце рівність

| | = |X| – |Y|,

або, що те саме,

|X \ Y| = |X| – |Y|.

За допомогою теореми 2 і властивостей операцій над множинами можна довести теорему про число елементів у об'єднанні трьох скінченних множин.

Теорема 4. Для довільних скінченних множин X, Y і Z має місце рівність

|X  Y  Z| = |X| + |Y| + |Z| – |X  Y| – |X  Z| – |Y  Z| + |X  Y  Z|.

Для того, щоб узагальнити наслідок 1 для кількох довільних скінченних множин, введемо деякі відношення між множинами. Говорять, що множини X1, X2,..., Xn,...

1) перетинаються, якщо вони мають спільні елементи, тобто існує принаймні один елемент, який належить усім цим множинам, отже,

X1  X2 ...  Xn ... ≠ ;

2) не перетинаються, якщо вони не мають спільних елементів, тобто не існує елемента, який належав би всім цим множинам, отже,

X1  X2 ...  Xn ... = ;

3) попарно не перетинаються, якщо Xi  Xj =  для всіх i та j таких, що i ≠ j, i, j = 1, 2, 3,....

Очевидно, якщо множини попарно не перетинаються, то вони не перетинаються, але коли множини не перетинаються, то не обов'язково вони попарно не перетинаються. Це видно для випадку трьох множин X, Y і Z, які зображено за допомогою кругів Ейлера на мал. 14.

Теорема 5 (правило суми). Якщо множини X1, X2,..., Xn – скінченні і попарно не перетинаються, то число елементів у їх об'єднанні дорівнює сумі числа елементів у цих множинах, тобто

|X1  X2 ...  Xn| = |X1| + |X2| +... + |Xn|.

Якщо множина Y є підмножиною множини X, то різниця множин X \ Y називається доповненням підмножини Y до множини X і позначається.

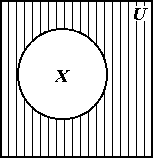
Різниця між універсальною множиною U і довільною її підмножиною X називається доповненням множини X і позначається. Очевидно, що означення доповнення можна сформулювати і без поняття різниці множин, а саме: якщо U – універсальна множина і X – її підмножина, то доповненням множини X називається множина, елементами якої є ті і тільки ті елементи універсальної множини U, що не належать множині X. Символічно це означення запишеться:

:= {x | x  U і x  X}.

Правило, за яким кожній підмножині X універсальної множини U ставиться у відповідність її доповнення, називається операцією доповнення множини.

Графічне зображення результатів операцій віднімання множин, доповнення підмножини до множини і доповнення множини за допомогою кругів Ейлера дано на мал. 3, де результати цих операцій заштриховано.

X \ Y

x

Мал. 3.

Порядок виконання операцій над множинами регулюється круглими дужками: спочатку виконуються операції у найглибших дужках, потім у наступних і т. д. Зовнішні дужки опускаються. Якщо ж дужки відсутні, то порядок виконання такий: доповнення до множини, що не є результатом операцій, переріз, об'єднання, віднімання.

9. комбінації без повторень.Число підмножин скінченної множини.

Комбінації без повторень

Означення. Комбінація по m елементів n-елементної множини – це її m-елементна підмножина.

Приклади.

1. При A={a, b, c} усі комбінації по два елементи – це підмножини {a,b}, {a,c}, {b,c}.

2. Розподіл n різних кульок по одній на кожний з m однакових ящиків, mn. Оскільки ящики однакові, то розподіл взаємно однозначно визначається підмножиною з m кульок, що розкладаються.

З кожної m-елементної комбінації елементів n-елементної множини можна утворити m! перестановок елементів цієї підмножини. Їх можна розглядати як розміщення по m елементів. Таким чином, кожні m! розміщень із тим самим складом, але різним порядком елементів відповідають одній комбінації. Звідси очевидно, що кількість комбінацій є =. Ця кількість позначається або.

Комбінацією із n елементів по m називається любий невпорядкований набір із m різних елементів, вибраних із загальної сукупності в n елементів.

В комбінаціях без повторень

набори відрізняються один від одного лише складом

і розраховуються по формулі(С=….)

Із приведених визначень видно, що результати підрахунків залежать від декількох факторів одночасно.

По-перше, від того, із якої кількості елементів можна складати набори.

По-друге, результат залежить від того, якої величини набори елементів потрібні.

Важливо також знати, чи являється суттєвий порядок елементів в наборі.

Якщо в умовах задачі є якісь особливості, то вони розв’язуються в першу чергу.

Число підмножин скінченної множини

Скінченна множина — це множина, кількість елементів якої є скінченна, тобто існує натуральне число k, що є числом елементів цієї множини. В протилежному випадку множина є нескінченною.

Визначення 2. Множина, що не має рівнопотужної з нею власної підмножини, а також порожня множина, називається скінченною

Основна теорема про скінченні множини

Скінченна множина не рівнопотужна жодній власній підмножині і власній надмножині.

Всіляка непорожня кінцева множина рівнопотужна одному і тільки одному відрізку натурального ряду

Будь-яка підмножина скінченної множини сама скінченна. Будь яка надмножина нескінченної множини сама нескінченна

Число елементів скінченної множини A завжди більше від числа елементів його власної підмножини B.

Доведення:

Нехай m - число єлементів з множини A, n - число елементів з множини B. Зауважимо, що n\ge m. Оскільки A\supset B, то A\ne 0, n>0, A\sim |1,m|. Також і m\ge n>0, отже B\sim |1,n| (1). При взаємно однозначному відображенні A на відрізок |1, m| множина B відображається також взаємно однозначно на деяку власну підмножина B' відрізка |1, m|, таким чином, B\sim b' (2). З B' \subset |1,m| та m\le n слідує B' \subset |1,n|(3). Проте з (1) та (2) слідує B' \sim |1,m|, що в силу (3) суперечить теоремі 1, т. я. відрізок |1, n| виявляється рівнопотужним своїй власній підмножині B '.

Дата добавления: 2014-12-16