Разложение определителя по элементам строки или столбца

Рассмотрим квадратную матрицу A n -го порядка.
Выберем i, j -ый элемент этой матрицы и вычеркнем i -ую строку и j -ый столбец. В результате мы получаем матрицу (n – 1)-го порядка, определитель которой называется минором элемента и обозначается символом M_{i j}:

.

Алгебраическое дополнение A_{i , j} элемента a_{i j} определяется формулой

.

Теорема о разложении определителя по элементам строки. Определитель матрицы A равен сумме произведений элементов строки на их алгебраические дополнения:

.

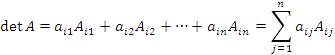Теорема о разложении определителя по элементам столбца. Определитель матрицы A равен сумме произведений элементов столбца на их алгебраические дополнения:

.

Теоремы о разложении определителя имеют важное значение в теоретических исследованиях. Они устанавливают, что проблема вычисления определителя n-го порядка сводится к проблеме вычисления n определителей (n –1)-го порядка.

Доказательство. По определению, детерминант матрицы A представляет собой сумму

(*)

по всем возможным перестановкам индексов, нумерующих столбцы.

Выберем произвольным образом некоторую строку, например, с номером i.
Один из элементов этой строки представлен в каждом произведении . Поэтому слагаемые суммы (*) можно перегруппировать, объединив в первую группу те, что содержат элемент a ₁₁ в качестве общего множителя, во вторую группу – члены, содержащие элемент a ₁₂ и т.д.
Другими словами, выражение (*) можно представить в виде линейной комбинации элементов a_{i j} (j = 1,2,…, n):

где

Покажем, что представляет собой алгебраическое дополнение элемента a_{i j}.
Перестановка преобразуется в перестановку посредством (i – 1) транспозиций элемента j с соседними элементами. В полученной перестановке элемент j образует (j – 1) инверсий с другими элементами.
Следовательно,

Однако сумма

представляет собой минор элемента a_{i j}.
Таким образом, и, следовательно, представляет собой алгебраическое дополнение элемента a_{i j}.

Поскольку 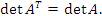, то тем самым доказана и Теорема о разложении определителя по элементам столбца.

Примеры:

1. Вычислить определитель матрицы третьего порядка разложением по элементам первой строки. Решение. Полученный результат находится в соответствии с правилом треугольников.

***

2. Вычислить определитель матрицы третьего порядка разложением по элементам второго столбца. Решение.

***

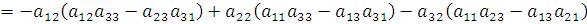
3. Вычислить определитель разложением по элементам первой строки. Решение.

***

4. Вычислить определитель разложением по элементам второго столбца. Решение.

Дата добавления: 2014-12-16