Теорема об обратной матрице

Лемма 2

Пусть A – квадратная матрица n -го порядка.

Утверждение. Если det A ¹0, то

(3)

где E – единичная матрица.

Доказательство. Запишем равенства (3) в терминах матричных элементов:

(4)

Это означает, что

(5)

Предположим, что i ¹ j. Тогда согласно Лемме 1

и

Мы показали, что результатом умножения (в том или ином порядке) матрицы A и присоединенной матрицы adj A является диагональная матрица. Остается доказать, что все диагональные элементы этой матрицы равны det A:

Этот результат становится очевидным, если воспользоваться теоремами о разложении определителя по элементам строки и столбца:

и

Теорема. Сингулярная матрица не имеет обратной матрицы. Для любой несингулярной матрицы A существует единственная обратная матрица:

Доказательство.

1. Предположим, что для матрицы A существует обратная матрица A ^-1. Тогда AA ^-1= E.

Учитывая, что определитель произведения матриц равен произведению определителей, получаем det A det A ^-1=1 и, следовательно, det A ¹0.

Это означает, что сингулярные матрицы не имеют обратных матриц.

1. Предположим теперь, что существуют две обратные матрицы, A ^-1и B ^-1.

Тогда AA ^-1= A ^-1 A = E и AB ^-1= B ^-1 A = E.

Используем эти равенства для преобразования матрицы B ^-1:

B ^-1= B ^-1 E ^-1= B ^-1 AA ^-1=(B ^-1 A) A ^-1= EA ^-1= A

что доказывает утверждение об единственности обратной матрицы.

1. В соответствии с Леммой 2

Следовательно,

Примеры:

1. Найти обратную матрицу для матрицы . Решение. Вычислим определитель матрицы: Поскольку , то обратная матрица существует. Далее найдем алгебраические дополнения всех элементов: , . Составим присоединенную матрицу : Таким образом, Проверка

***

2. Найти обратную матрицу для матрицы Решение. Вычисляем определитель: Матрица A является сингулярной и, следовательно, обратная матрица не существует.

***

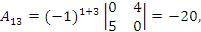3. Найти обратную матрицу для матрицы Решение. 1) Для вычисления определителя прибавим ко второй строке удвоенную первую; затем разложим определитель по элементам второго столбца: 2) Найдем алгебраические дополнения элементов матрицы: Составим присоединенную матрицу : Делением присоединенной матрицы на det A получаем обратную матрицу: Проверка: 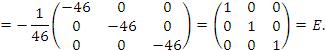Аналогично,  

***

3. Даны матрицы и . Решить матричное уравнение (*) Решение. Поскольку , то матрица A является неособенной и существует обратная матрица . Умножим обе части уравнения (*) на матрицу справа: Составим присоединенную матрицу : Следовательно, Тогда Проверка:

Дата добавления: 2014-12-16