Приняв r » rж, имеем 2 страница

Местные прибыли обеспечивают питание примыкающих к ним участков отливки на определенную длину, называемую зоной дей­ствия прибыли. Зоны действия прибылей определяют на основа­нии эмпирических данных в зависимости от толщины питаемого узла (рис. 3.20). Например, для прибылей, установленных по схеме рис. 3.20, а, зона действия прибыли для сплава латуни рав­на А = 4Т, для силуминов А = 3Т. Вследствие влияния концевого эффекта (нарастание твердой корки на торцевой поверхности отливки) зона действия прибыли, установленной у края отливки (рис. 3.20, б), увеличивается и равна для латуни А = 5Т, а для силумина А = 6,5Т. Таким образом, расстояние между местными прибылями l не должно превышать удвоенную величину зоны действия прибыли, т. е. l £ 2А. Если l > 2A, то в зависимости от характера затвердевания сплава за пределами зоны влияния при­былей в отливках будут образовываться усадочные дефекты в виде раковин или усадочной пористости.

Для протяженных отливок с большим отношением длины к толщине или ширине целесообразно применять боковые прибыли (рис. 3.21). Боковые прибыли применяют также при изготовлении отливок из сплавов, плохо обрабатывающихся резанием (сталь 110Г13Л, ковкий чугун и т. п.).

Преимущества боковых прибылей по сравнению с верхними сводятся к возможности питания меньшими по объему прибы­лями протяженных отливок, снижения трудоемкости удаления прибылей от отливок (их можно отламывать или отрезать при значительно меньшей площади резки), уменьшения трудоемкости механической обработки подприбыльных участков отливки и т. д. Место соединения боковой прибыли с отливкой называется шейкой прибыли. Следует отметить, что шейка прибыли может иметь приведенную толщину стенки, существенно меньшую, чем у отливки. Это объясняется влиянием прогрева формы около шейки прибыли протекающим через нее металлом, так как залив­ка в данных случаях осуществляется через прибыль (см. рис. 3.21). К моменту окончания заливки температура формы около шейки прибыли наибольшая и убывает по мере удаления от прибыли, что способствует направленности затвердевания.

Иногда боковые прибыли устанавливают на термических уз­лах отливки, расположенных на разной высоте. Такие прибыли называют потайными (рис. 3.22).

Для того чтобы прибыль работала так, как показано на рис. 3.22, необходимо обеспечить в ней некоторый баланс давле­ния жидкого металла. Потайные прибыли являются закрытыми. Поэтому с момента образования на их поверхностях достаточно прочной корки затвердевшего металла жидкий расплав отсекает­ся от внешнего атмосферного давления. Вследствие действия ат­мосферного давления со стороны открытой прибыли и увеличиваю­щегося к низу отливки гидростатического давления, равного, например, для нижней прибыли rgH_н, перепад давлении будет направлен вверх, т. е. он будет обеспечивать перенос металла в прибыль, а не из прибыли в отливку. В этом случае установка потайных прибылей приведет к увеличению объема верхней при­были, так как она должна компенсировать дополнительно усадку сплава в этой прибыли. Прибыли начнут действовать только после затвердевания сечений В — В и А — А.

Для улучшения действия прибылей в них устанавливают газо­проницаемые стерженьки, передающие внутрь прибыли атмосфер­ное давление (см. рис. 3.22). Однако гидростатическое давление rgH_н и rgH_с. в этом случае все равно оказывается некомпенсированным. Для обеспечения нужного баланса давлений целесооб­разно создать в прибылях повышенное газовое давление, равное для нижней и средней прибыли соответственно Р_а + rgH_н и P_a. + rgH_с. В этом случае все прибыли с самого начала будут действовать независимо: каждая будет питать свой узел.

По конфигурации различают шаровые или полушаровые, ци­линдрические, конусные, овальные, прямоугольные прибыли (рис. 3.23).

С точки зрения тепловых условий работы конфигурация при­были должна обеспечить при данном ее объеме минимальную поверхность охлаждения. Известно, что этому условию удовлет­воряет шар. Однако такие прибыли сложно выполнить в форме, поэтому наиболее широко применяют полушаровые закрытые прибыли или конические открытые прибыли. Часто используют прибыли, имеющие овальное горизонтальное сечение. Следует за­метить, что при конструировании прибылей их конфигурация всегда увязывается с конфигурацией питаемого узла. Более де­тально вопросы конструирования прибылей изучаются в техно­логических курсах.

Рассмотрим основные принципы расчета прибылей. Прежде всего, прибыль должна иметь запас сплава, обеспечивающий ком­пенсацию объемной усадки отливки и самой прибыли. Так как в процессе формирования отливки на стенках прибыли происходит образование затвердевшей корки, то объем прибыли равен

V_ПР = V_УС.Р + V_З.К

V_УС.Р = e_V(V_ОТЛ + V_ПР)

где V_yc.p — объем усадочной раковины; V_з.к — объем затвердев­шего сплава в прибыли. Объем затвердевшего металла зависит от тепловых условий работы прибыли и гидродинамических усло­вий, определяющих скорость опускания сплава в прибыли. Чем больше интенсивность теплоотвода от прибыли и чем меньше ско­рость опускания уровня сплава в ней, тем больше V_з.к. Как сле­дует из полученного в предыдущем разделе уравнения неразрыв­ности потока питающего жидкого сплава, скорость опускания сплава в прибыли непосредственно связана со скоростью выделе­ния в расплаве отливки твердой фазы dy/dt. Чем больше dy/dt, тем с большей скоростью может опускаться сплав в прибыли.

Однако эта потенциальная возможность в зависимости от ха­рактера затвердевания используется в разной степени. При после­довательном затвердевании, за исключением питания осевых участ­ков отливки, жидкий расплав полностью и практически мгновен­но компенсирует появившийся в отливке дефицит питания. При объемном затвердевании в условиях фильтрационного и суспензионного питания скорость питающего потока существенно за­висит от прилагаемого к расплаву давления. Если давление не­достаточно велико, то, несмотря на наличие дефицита питания, расплав из прибыли не будет израсходован. При этом в отливке образуется большая усадочная пористость.

Коэффициент полезного использования металла в прибыли — b = V_yc.p/V_пp. Здесь, строго говоря, в величину V_yc.p следует вклю­чать весь дефицит питания, а не только собственно объем усадоч­ной раковины. Величина b зависит от конфигурации прибыли, прилагаемого к расплаву давления и тепловых условий работы при­были. Для обычных открытых прибылей b = 0,1, для закрытых прибылей b = 0,11 — 0,15, для прибылей с газовым давлением b = 0,13 ¸ 0,2. Применение подогрева сплава в прибылях позво­ляет значительно повысить b и снизить расход металла на при­были. Если принять, что коэффициент b известен, то можно рас­считать объем прибыли по простой формуле, впервые полученной И. Пржибылом:

V_УС.Р = e_V(V_ОТЛ + V_ПР)

V_УС.Р = bV_ПР

bV_ПР = e_VV_ОТЛ + e_VV_ПР

Отсюда V_ПР(b - e_V) = e_VV_ОТЛ или

V_ПР=e_VV_ОТЛ/(b-e_V)

Здесь V_отл — объем узла отливки, питаемого данной прибылью. Высота прибыли принимается равной ее диаметру или несколько больше.

Классический метод расчета прибылей сводится к определе­нию глубины проникновения усадочной раковины в системе от­ливка — прибыль. Высоту прибыли устанавливают, исходя из обеспечения полного расположения усадочной раковины в при­были с некоторым запасом.

В основе математического расчета прибылей на ЭВМ лежит балансный принцип расхода сплава из прибыли на питание и затвердевание на ее стенках (см. гл. 6.3 и 6.4) при определении контура усадочной раковины. Кроме балансного уравнения мо­дель включает дифференциальные уравнения, описывающие кине­тику затвердевания сплава в отливке и прибыли. Навыки машин­ного расчета прибылей студент должен получить на практических занятиях.

Приведенная формула (3.12) получена для плоской отливки толщиной 2Ro при следующих допущениях:

1) фронт солидуса в отливке продвигается по закону, а В Прибыли

2) толщина прибыли равна 2R_п > 2R₀;

3) вся усадка приведена к температуре солидуса и включает усадку в жидком состоянии и при затвердевании.

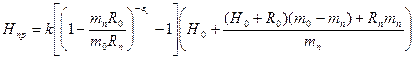
где A—коэффициент запаса (обычно k = 1,5 ¸ 3). Как правило, отношение приведенных размеров прибыли и отливки принимают в пределах R_п/R₀ = 1,15 ¸ 1,5.

Выполним расчет высоты прибыли для стальной отливки: R_п/R₀ = 1,25; R₀ = 15 см; R_п = 18,75 см; e_V = 0,06; высота отливки H₀ = 40 см; m₀ = 0,085 cм/с^1/2; m_п = 0,060 cм/с^1/2.

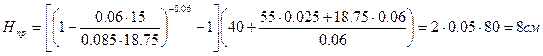
Для того чтобы уменьшить m_п по сравнению с m ₀, необходимо применить подвод сплава в прибыль, использовать смесь с мень­шим коэффициентом аккумуляции тепла, а для крупных отливок осуществить доливку металла в прибыль из ковша. В условиях рассмотренного примера при m_п = m₀ = 0,085 высота прибыли равна H_пр = 2×0,11×95 = 21 см. Видно, что уменьшение интенсив­ности затвердевания сплава в прибыли приводит к уменьшению объема прибыли.

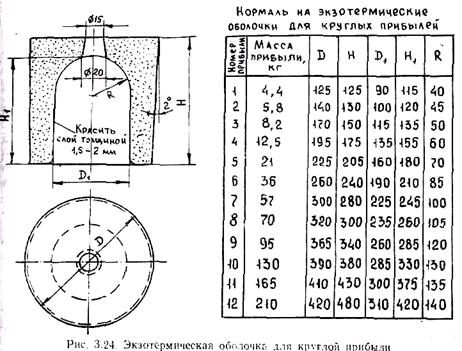
Существенного уменьшения затвердевшего в прибыли сплава, а следовательно, и необходимого ее объема можно добиться, при­меняя обогрев прибылей экзотермическими смесями. Из этих сме­сей изготовляют стаканы или втулки, которые устанавливают в прибыльные части полости формы (рис. 3.24).

Существуют различные по составу экзотермические смеси. Экзотермическая реакция, сопровождающаяся большим выделе­нием тепла, представляет собой реакцию восстановления окиси железа алюминием (алюмотермия) или кремнием (силикотермия):

Fе₂О₃ + 2Аl = Аl₂O₃ + 2Fe + Q₁,

2Fе₂О₃ + 3Si = 3SiO₂ + 4Fe + Q₂.

Кроме алюминиевого порошка, ферросилиция и окалины смесь содержит связующее для придания ей прочности во влажном со­стоянии и после сушки, а также древесные опилки, гипс, моло­тый шамот, глину для обеспечения газопроницаемости смеси и регулирования интенсивности экзотермической реакции.

Расчет экзотермических прибылей сводится к определению номера нормализованной экзотермической оболочки для оформле­ния прибыли. Подбор оболочек осуществляют по массе прибыли m_пр. Массу прибыли находят по специально разработанным но­мограммам. Принципиально ее можно определить по приведенной выше формуле И. Пржибыла, приняв b = 0,2 ¸ 0,25, или а ис­пользованием полученной выше формулы для расчета высоты прибыли, приняв константу затвердевания в 1,5—2 раза мень­шей по сравнению с обычной песчаной формой. По массе прибыли находят размеры экзотермических оболочек по нормализованным таблицам (см., например, рис. 3.24).

Выше было сказано о большой роли в повышении эффектив­ности работы прибылей и их экономичности перепада давлений, действующего на кристаллизующийся расплав. Так, П. И. Ямшановьш были предложены прибыли с повышенным газовым давлени­ем, создаваемым диссоциацией при высоких температурах мела, карбоната магния или цинка:

СаСО₃ = СаО + СO₂ при Т ³ 825°С;

MgCO₃ = MgO + CO₂ при Т ³ 350°С;

ZnCO₃ = ZnO + CO₂ при Т ³ 300°С.

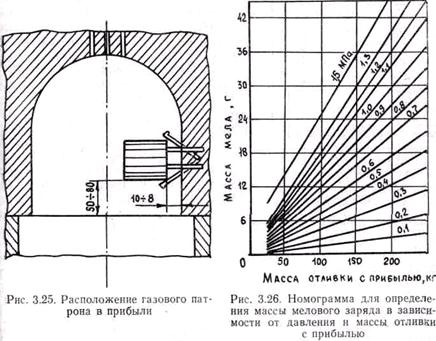
Определенная масса данных веществ помещается в специаль­ный патрон, устанавливаемый внутрь закрытой прибыли (рис. 3.25). Оболочки и крышки патронов изготавливают уплот­нением в металлических ящиках смесей, состоящих из глины, мо­лотого шамота и древесных опилок, добавляемых для повышения газопроницаемости оболочки. Оболочки сушат при 100 - 110 ⁰C и обжигают при 350 °С. Главное требование к оболочке сводится к тому, что ее толщина должна обеспечивать прогрев помещен­ного в нее наполнителя до температуры диссоциации не раньше, чем на стенках прибыли вырастет достаточно прочная корка за­твердевшего сплава, способная выдержать повышенное давление.

Параметры прибыли, патрона и массу заряда определяют по эм­пирически разработанным номограммам. Массу прибыли можно определить, например, по формуле И. Пржибыла, приняв в ней b = 0,13 ¸ 0,20.

В зависимости от массы прибыли и создаваемого давления по номограмме, приведенной на рис. 3.26, определяют массу мела, помещенного в патрон.

Толщину стенки патрона и его размеры определяют по специальным номограммам. Применение прибылей газового давления позволяет не только повысить выход годного, но и существенно снизить пористость отливок.

Детальное изучение методов расчета и конструирование при­былей для отливок из различных сплавов предусмотрено в соот­ветствующих технологических курсах. Приближенные аналитиче­ские и эмпирические формулы для расчета прибылей получены А. А. Рыжиковым, Б. Б. Гуляевым, Ф. Ф. Василевским, Н. Бишопом и В. Джонсоном, Р. Намюром и др. Главной особенностью этих методов является их ориентация на последовательно затвер­девающие сплавы и усадочные дефекты, проявляющиеся главным образом в виде усадочной раковины. Их применение к объемно затвердевающим сплавам неправомерно, так как усадочная рако­вина в этих случаях очень мала по объему по сравнению с объ­емом пор.

Методику расчета прибылей при объемном затвердевании спла­ва можно построить, исходя из следующих принципов:

1) прибыль должна быть достаточно теплоизолирована (на­пример, при кокильном литье стенки прибыльных частей оклеи­ваются листовым асбестом или по­крываются специальной краской). При этом должно выполняться условие: продолжительность снятия перегрева в центре прибыли должна быть не меньше продолжительности затверде­вания отливки;

2) объем прибыли должен быть достаточным для компенсации объем­ной усадки отливки и прибыли. Его можно найти по формуле и. Пржибыла, приняв, в ней b = 0,2 ¸ 0,25;

3) высота прибыли и прилагаемое к сплаву в прибыли давление Р₀должны обеспечить фильтрационное питание отливки, гарантирующее за­данный уровень пористости в ней. Дав­ление (Р₀ + rgH_п), обеспечивающее заданное значение пористости, в первом приближении можно найти с использованием формул, полученных в разд. 3.

В заключение рассмотрим прибыли с облегченным отделени­ем от отливок (рис. 3.27).

Между прибылью и питаемым узлом устанавливают перего­родку в виде керамической пластины. Важнейшим требовани­ем является совпадение оси отверстия в перегородке с термиче­скими центрами прибыли и отливки. При нарушении этого требо­вания в отливке образуется усадочная раковина. Параметры пере­городки и размеры отверстия выбирают таким образом, чтобы она быстро прогревалась до температур, исключающих образо­вание на ее поверхностях затвердевшего металла. Обычно диа­метр прибыли определяют по формуле

где d_вп — диаметр окружности, вписанной в термический узел пи­таемой отливки, дм; Д_пр — диаметр прибыли, дм; Q — масса пи­таемого узла, кг. Высоту прибыли принимают равной (1 ¸ 1,5)Дпр. Толщину пластины и диаметр отверстия в ней определяют в за­висимости от значения диаметра прибыли по соответствующим таблицам.

ГЛАВА 3.4. ЛИТЕЙНЫЕ НАПРЯЖЕНИЯ И ДЕФОРМАЦИИ В ОТЛИВКАХ

В предыдущей главе были рассмотрены явления, связанные с развитием в процессе формирования отливки объемной усадки. Пока сплав, имеющий температуру внутри интервала кристалли­зации, сохраняет характерную для жидкости текучесть, усадочные явления проявляются как объемные. Линейные размеры при этом определяются, как и у любой жидкости в условиях действия зем­ного тяготения, размерами сосуда, в котором она находится. В процессе охлаждения уменьшается только объем. Собственно линейная усадка, т. е. независимое уменьшение линейных раз­меров отливки при понижении ее температуры, начинает разви­ваться только после потери сплавом текучести в конкретных си­ловых условиях формирования отливки. По предложению И. И. Новикова, с этой точки зрения интервал кристаллизации сплава можно разбить на две зоны: жидкотвердую и твердожидкую. В жидкотвердой зоне (при Т_у < T £ T_л, где Т_у — темпера­турная граница частей) сплав сохраняет текучесть. При Т_c £ Т £ Т_у в твердожидкой зоне интервала кристаллизации в спла­ве содержится количество твердой фазы, необходимое для обра­зования каркаса, проявляющего свойство твердого тела сохранять ранее приданную ему конфигурацию. Эту нижнюю часть интер­вала кристаллизации А. А. Бочвар назвал эффективным интер­валом кристаллизации сплава (ЭИК). В пределах ЭИК. кристал­литы образуют остов отливки, но частично отделены друг от дру­га прослойками расплава. Так как при температуре Т < Т_у сплав теряет текучесть, то, начиная с Т = Т_у, в отливке будет происхо­дить линейная усадка. При Т > Т_у реализуется только объемная усадка.

3.4.1. ГОРЯЧИЕ ТРЕЩИНЫ В ОТЛИВКАХ

Если свободную линейную усадку отливки затормозить, то в ней возникнут напряжения растяжения. На рис. 3.28 показана схема формы для изготовления отливки «крышка». При темпера­туре Т = Т_у размер отливки l₀ равен размеру формы. Если участок формы между боковыми стенками отливки абсолютно податлив, то при охлаждении отливки до температуры Т произойдет ее пол­ная усадка и длина отливки будет равна l = l₀(1 - a_т(T_у - Т)). При этом никаких напряжений в ней не возникает. Если форма абсолютно неподатлива, то отливка сохранит размер l₀, т. е. ее длина будет больше того значения, которое она должна иметь при температуре Т, на величину Δl = l₀ – l = l₀ – l₀(1 - a_т(T_у - Т)) = l₀a_т(T_у - Т). Таким образом, отливка получит в данном слу­чае относительную деформацию растяжения e_у = Δl/l₀ = a_т(T_у - Т). Если форма обладает некоторой податливостью, то относительная деформация растяжения уменьшается на величину e_п, где e_п - относительная деформация формы за время усадки. Если учесть расширение участка формы между ребрами вследствие ее про­грева, то результирующая относительная деформация отливки будет удовлетворять равенству

e = e_У - e_П + e_Р

где e_р — относительная деформация формы вследствие ее тепло­вого расширения.

С уменьшением температуры внутри ЭИК увеличивается e_у и e_р, т. е. относительная деформация отливки e растет, достигая при Т = Т_с наибольшего значения e_mах = a_т(T_у - Т), если прене­бречь величинами e_п и e_р. В случае, если деформация растяжения отливки e превзойдет деформационную способность e₀, в отливке возникнет горячая трещина.

Таким образом, необходимое условие образования горячих тре­щин сводится к торможению свободной линейной усадки сплава во время его затвердевания в литейной форме. Достаточное усло­вие выражает неравенство e ³ e₀, т. е. образование трещин проис­ходит в момент превышения относительной деформацией сплава eего деформационной способности e₀. Таким образом, для образо­вания трещины необходимо, чтобы e_у - e_п + e_р ³ e₀.

Из этого неравенства вытекают следующие пути борьбы с горячими трещинами:

1) улучшение податливости форм, т. е. увеличение e_п;

2) совершенствование конструкции отливки с целью исклю­чения торможения линейной усадки;

3) синтез сплавов, обладающих низкими значениями отно­сительной линейной усадки (уменьшение a_т) и высокой дефор­мационной способностью e₀.

Комплекс конкретных технологических мероприятий, направ­ленных на исключение трещин в отливках, будет рассмотрен в конце данной главы.

Особое место среди данных мероприятий занимает повышение сопротивляемости сплавов образованию горячих трещин. Под термином «горячеломкость сплавов» понимают их технологическое свойство образовывать горячие трещины в отливках. Для определения этого свойства применяют различные технологические пробы (рис. 3.29). Горячеломкость сплава характеризуется зна­чением длины образца L₀, начиная с которой в отливках образу­ются трещины. Чем больше L₀, тем меньше сплав склонен к тре­щинам, т. е. тем меньше его горячеломкость.

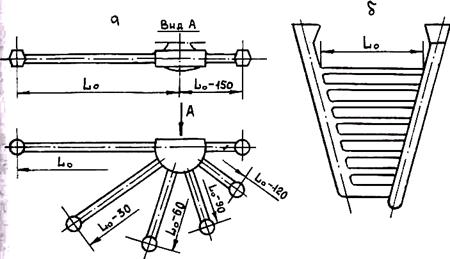
Рис. 3.29. Конструкции проб на горячеломкость сплавов:

a — проба А. Татюра; б — проба И. Н. Прохорова

Для примера можно привести так называемую кольцевую пробу, которая представляет собой кольцо, залитое в кокиль с металлическим стержнем. Показателем горячеломкости является отношение протяженности самой большой трещины к радиально­му сечению кольца, выраженное в процентах. Например, для спла­ва Аl — Si в зависимости от содержания кремния этот показатель изменяется в пределах от 10 до 50%. Часто для характеристики горячеломкости изготовляют из сплава несколько колец разной толщины (от 5 до 42,5 мм). Критерием горячеломкости в данном случае служит наибольшая толщина кольца, выраженная в мил­лиметрах, при которой образуется трещина. Чем меньше толщина кольца, тем меньше склонен сплав к горячим трещинам. Выбор той или иной пробы зависит от ее чувствительности для данной группы сплавов. Поэтому более подробно методика оценки горячеломкости сплавов будет рассмотрена в технологических курсах.

3.4.1.1. ТЕОРИЯ ГОРЯЧЕЛОМКОСТИ СПЛАВОВ

Одним из первых систематические исследования горячеломкости сплавов проводил А. А. Бочвар. По его мнению, горячеломкость сплавов связана с шириной ЭИК. С увеличением шири­ны ЭИК увеличивается склонность сплава к образованию горячих трещин (рис. 3.30).

В соответствии с теорией горячеломкости, разработанной Н. Н. Прохоровым, деформационная способность сплавов e₀ опре­деляется пластической деформацией растяжения сплавов e_пл в момент разрушения при температуре солидуса. Механизм обра­зования горячих трещин, по Н. Н. Прохорову, сводится к следующему. Расплав в эффективном интервале температур представ­ляет собой кристаллиты, отделенные друг от друга тонкими про­слойками жидкого сплава. Принятая Н. Н. Прохоровым упро­щенная схема строения сплава в ЭИК приведена на рис. 3.31.

При температуре Т_у начала свободной линейной усадки жидко-твердый расплав теряет свою подвижность как единое целое.

На схеме показаны кубические кристаллиты, разделенные друг от друга прослойками жидкого сплава. При полном торможении усадки размер l₀ остается в процессе охлаждения сплава постоян­ным. В процессе охлаждения сплава размер прослоек d будет уменьшаться. При этом, как было показано в разд. 2, вследствие объемной усадки кристаллизующейся жидкости ее давление бу­дет иметь тенденцию к уменьшению. Так как система лишена подвижности вдоль размера l₀, возможно лишь перемещение кри­сталлитов навстречу друг другу в перпендикулярном направле­нии под действием возникающего перепада давлений. При этом жидкий сплав из области вертикальных прослоек перемещается в область горизонтальных, компенсируя там объемную усадку. Подобный процесс развивается до полного исчезновения верти­кальных (в соответствии со схемой) прослоек (рис. 3.31, б).

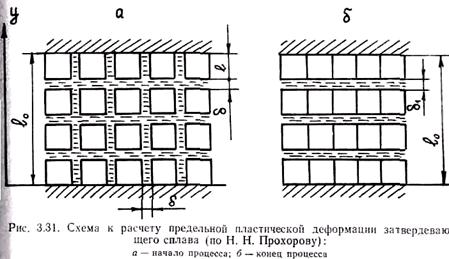
Дальнейшая усадка сплава будет сопровождаться порообра­зованием и формированием трещины. Н. Н. Прохоров для при­веденной на рис. 3.32 структуры сплава выполнил следующий вы­вод формулы для расчета его деформационной способности в ус­ловиях одноосного изотермического растяжения вдоль оси у. Объем жидкого сплава, приходящегося на один кристаллит в начале деформирования, равен (l + f)³ – l³. После деформиро­вания объем жидкости равен l²(l + f₁) – l³ Приравняв эти выра­жения, получим (l + f)³ = l²(l + f₁). Отсюда f₁ = 3f + 3f²/l + f³/l². Относительная деформация растяжения равна e_пл =(f₁ - f) / (1 + f) = f(2 + f/l)/l

Доля твердой фазы в сплаве при температуре Т равна

Отсюда получаем j/l = 1/y^1/3 - 1. С учетом этого

e_ПЛ = 1/j^2/3 – 1 (3.13)

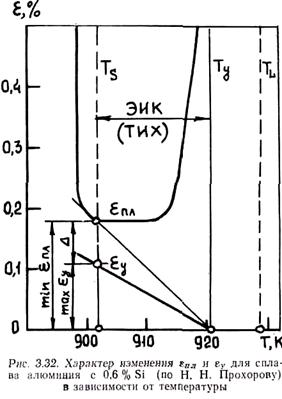
Из формулы И. Н. Прохорова следует, что по мере снижения температуры уменьшается деформационная способность сплава e_пл, так как при этом доля твердой фазы y увеличивается. При температуре солидуса y = 1 и e_пл = 0.

На рис. 3.32 приведен характер зависимости e_пл от темпера­туры внутри интервала кристаллизации, определенный экспери­ментально для сплава алюминия с 0,6 % Si. Здесь же приведена зависимость относительной свободной линейной усадки e_у от тем­пературы в соответствии с формулой e_у = a_тв(T_у - Т). Величину Δ = min (e_пл - e_у) Н. Н. Прохоров назвал запасом пластичности сплава, а интервал температур (Т_у - Т_c) — температурным интер­валом

хрупкости (ТИХ). Видно, что в отличие от предсказывае­мого теорией Н. Н. Прохорова величина интер­валом при температуре солидуса не равна нулю и при дальнейшем охлаждении увеличива­ется. Многочисленные эксперименты показывают, что температур­ный интервал горячеломкости (ТИГЛ) не обязательно примыкает к температуре солидуса, а может иногда охватывать весь тем­пературный интервал хладноломкости.

Очевидно, что реальный механизм образования горячих тре­щин значительно сложнее рассмотренного выше. Прежде всего, кристаллиты имеют гораздо более сложное строение, чем пока­зано на рис. 3.31. Чаще всего они имеют вид разветвленных, сцепленных друг с другом дендритов. При нагружении происхо­дит не только рассмотренная выше циркуляция жидкого сплава, но и непосредственная деформация кристаллитов. Для выяснения вопроса о деформационной способности сплава необходимо уста­новить соответствующий его поведению реологический закон. Простейшие реологические модели были рассмотрены в разд. 1.

3.4.1.2. РЕОЛОГИЧЕСКАЯ МОДЕЛЬ СПЛАВА В ИНТЕРВАЛЕ КРИСТАЛЛИЗАЦИИ

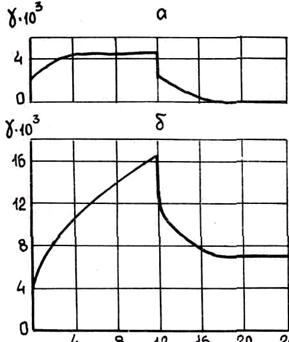
Систематические исследования реологических свойств сплавов. в интервале кристаллизации были выполнены Г. Ф. Баландиным и Л. П. Каширцевым. На основе анализа экспериментальных дан­ных, полученных для алюминиевых сплавов, они установили, что реологическое поведение сплавов в интервале кристаллизации отвечает поведению сложного тела, состоящего из последователь­но соединенных тел Бингама и Кельвина, т. е. реологическая фор­мула сплава — Т = В - К. Тела Бингама и Кельвина были рас­смотрены в разд. 1. Реологическая схема сплава приведена на рис. 1.36. На рис. 3.33 показаны кривые деформации кристалли­зующегося алюминия А7 под действием постоянной нагрузки. Используя схему, приведенную на рис. 1.36, получим реологические уравнения, описывающие поведение сплавов в интервале кристал­лизации. Эти уравнения впервые были получены Л. П. Кашир­цевым. На схеме последовательно соединены три тела: тело Гука Н₁, тело (S/N₁) и тело Кельвина (H₂/N₂). Поэтому суммарная де­формация всего тела у равна сумме деформаций этих трех тел, т. е.

g = g₁ + g₂ + g₃

С другой стороны, используя реологические законы указан­ных тел, полученные в разд. 2, можно записать следующие урав­нения для напряжений:

Дата добавления: 2014-12-16