Приняв r » rж, имеем 3 страница

t = g₁G₁ (3.14)

t =g₃G₂ + h₂g₃ (3.15)

Для тела (S/N₁) запишем

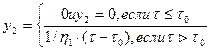
Приведенные уравнения полностью описывают реологическое поведение сплава. Однако, для того чтобы замкнуть эту систему уравнений, необходимо для каждого сплава знать величину предельного напряжения сдвига то, модуля упругости при сдвиге G, модуля G₂, пластической вязкости h₁ и псевдовязкости Кельви­на h₂ как функции температуры. По данным Л. П. Каширцева, все указанные величины в интервале кристаллизации по мере приближения к температуре солидуса резко возрастают. Пример температурных зависимостей реологических характеристик для сплава алюминия с 0,6 % Si приведен на рис. 3.34.

Из системы уравнений (3.14) — (3.15) следует, что деформация сплава является суммой упругой деформации g₁ пластической остаточной деформации g₂ и деформации упругого последействия (обратимой пластической деформации) g₃. Для того чтобы опре­делить, какая из этих видов деформаций влияет на деформацион­ную способность сплава, выполним, следуя Л. П. Каширцеву, от­носительное сравнение их величин.

Уравнения (3.14) — (3.17) позволяют при заданном значении напряжения t определить развитие как суммарной деформации сплава, так и отдельных ее составляющих, если известны реоло­гические характеристики сплава при данной температуре.

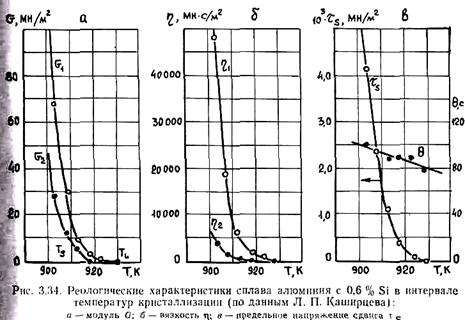
При анализе деформационной способности сплавов чаще всего образцы сплава при данной температуре внутри интервала кри­сталлизации подвергают механическим испытаниям при постоян­ной скорости деформации.

Пусть сплав испытывается при постоянной скорости деформа­ции g = VД = const. Преобразуем исходную систему уравнений:

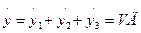
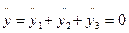
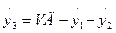
Подставив в это выражение приведенные выше выражения для g₃ и g₃ получим следующие дифференциальные уравнения:

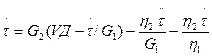
Найдем зависимость т от времени при t < Т₀. Преобразуем со­ответствующее уравнение:

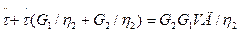
Очевидно следующее начальное условие: при t = 0 t = 0. Най­дем значение t при t = 0. Так как t = 0, то g₃G₂ + h₂g₃ = 0. При t = 0 g₃ = 0, поэтому, как следует из последнего выражения, g₃ = 0, g = g₁ + g₃ = g₁ = VД. Поэтому t = VД×G₁.

Решив это уравнение при данных начальных условиях, получаем формулу

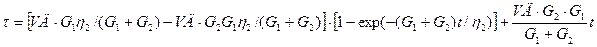
Как показали расчеты с использованием значений реологиче­ских характеристик алюминиевых сплавов, полученных Л. П. Каширцевым, (G₁ + G₂)/h₂ << 1. Поэтому, разлагая экспоненту в ряд с точностью до второго члена, получаем

exp(-(G₁ + G₂)t/h₂)» 1 – (G1 + G2) t/h₂

С учетом этого получаем упрощенное выражение t = VД×G₁×t которое позволяет сделать вывод, что деформацией упругого последействия можно пренебречь в первом приближении. Время, в течение которого напряжение достигает значения предельного напряжения сдвига t₀, равно t₀ = r₀/(VД×G₁).

Решим уравнение для t > 0. Преобразуем его к виду

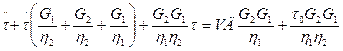
Сформулируем начальные условия: при t = t₀ t = t₀, t = t(t = t₀). Определим t(t = t₀). Так как при t = t₀ g₂ = 0, g₃ = 0 (пренебрегаем развитием упругого последействия при t £ t), то g = g₁ = VД. Поэтому t (t = t₀) = VД × G₁.

Решая дифференциальное уравнение при данных начальных ус­ловиях, получаем

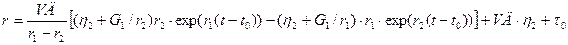
где

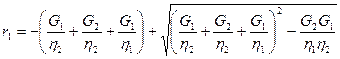
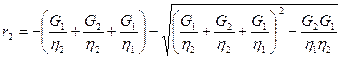
Так как (G₁/h₂ + G₂/h₂ + G₁/h₁) << 1, то, приняв exp(r₁(t - t₀))» 1 + r₁(t – t₀) и exp(r₂(t – t₀))» 1 + r₂(t – t₀), после преобразований получим

t = t₀ + G₁VД × (t - t₀)

Из этого выражения вытекает, что если r₁(t – t₀) << 1, то пла­стической деформацией и деформацией упругого последействия можно пренебречь по сравнению с упругой. Для того чтобы ре­шить вопрос строго, необходимо из полученной точной формулы найти время, за которое напряжение t достигнет предела проч­ности сплава t_пр, вычислить все виды деформаций, накопленные к этому моменту времени, и сравнить их. Подобные расчеты с применением численных методов на ЭВМ выполнены Л. П. Каширцевым для случая испытания образцов из большого числа алюминиевых сплавов на растяжение. На рис. 3.35 приведены расчетные кривые изменения предельной деформационной способ­ности сплава алюминия с 0,6%Si в интервале его кристаллиза­ции при скорости деформации e=0,00015 с^-1.

Видно, что пластическая деформация e₃ и деформация упру­гого последействия e₂ более чем на порядок меньше упругой деформации e₁. Поэтому приближенно можно принять, что деформа­ционную способность сплавов в интервале кристаллизации необ­ходимо оценивать не по пластической, а по упругой деформации, т. е. e₀» e₁. Фактическим подтверждением этого вывода является то, что разрушение сплава при образовании горячих трещин носит хрупкий характер.

Вывод о том, что пластическая деформация вблизи темпера­туры солидуса мала, следует из полученной выше формулы Н. Н. Прохорова, из которой видно, что при температуре

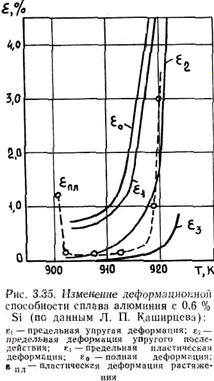
солиду­са пластическая деформация равна нулю. Сравнение деформаци­онной способности сплавов e₀ с относительной свободной усадкой e_у (см. рис. 3.35) показывает, что e_у < e₀. Поэтому величина Δ = min e₀ – mах e_у всегда положительна. Отсюда можно сделать вывод, что даже при полном затруднении горячие трещины не должны образовываться, что противоречит действительности. Сле­довательно, причины образования горячих трещин нужно искать в другом направлении.

3.4.1.3. МЕХАНИЗМ ОБРАЗОВАНИЯ ГОРЯЧИХ ТРЕЩИН

Изложенная выше теория рассматривает сплав с однородным температурным полем в объеме отливки. Все реологические харак­теристики во всех точках сплава одинаковы, поэтому весь объем испытывает однородно распределенные деформации. В реальной отливке скорость охлаждения ее отдельных элементов различна.

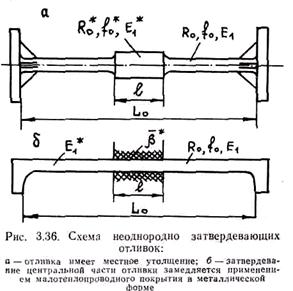
При этом неоднородно развивается усадка, и реологические свой­ства распределены в отливке существенно неоднородно. Поэтому в отдельных элементах отливки, которые затвердевают медленнее других, могут локализоваться усадочные процессы. Величина усадки e_у при этом сильно возрастает и может превысить деформа­ционную способность e₀, что приведет к образованию горячих трещин.

Поясним это на следующем примере. На рис. 3.36 приведена отливка, содержащая в середине длины утолщение, а также от­ливка, затвердевание центральной части которой замедлено при­менением малотеплопроводного покрытия металлической формы. Примем, что модули упругости Е в утолщенной и теплоизолированнои частях отливок значительно меньше, чем в остальных частях, так как модуль упругости существенно зависит от темпе­ратуры (с увеличением температуры он уменьшается). При этом крайние участки отливки можно считать жесткими. В сечении, разделяющем центральную и периферийную части, действуют на­пряжения s₁ = E₁×Δl₁/(L₀ - l) и s₂ = E₂×Δl₂/l, где Δl₁ — деформация периферийной части; Δl₂ — деформация центральной части. Очевидно, что исходя из условий равновесия s₁ = s₂ или E₁×Δl₁/(L₀ - l) = E₂×Δl₂/l. С другой стороны, сумма деформаций Δl₁ и Δl₂ должна быть равна свободной усадке всей отливки:

∆l₁ + ∆l₂ = a_св×[(L₀ – l)×(T_у – T₁) + l(Т_у – Т₂),

где T₁ и Т₂ — температура периферийных и центральной частей отливки (Т₂ > T₁). Решив совместно оба приведенных уравнения, получим следующее выражение для относительной усадки цент­ральной части:

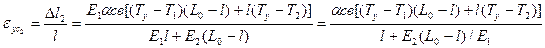
Очевидно, что при E₁ = E₂ и Т₂ = Т₁ e_ус2 = a_св(T_у - Т ), т. е. в центральном элементе относительная усадка равна относитель­ной усадке сплава. С уменьшением отношения E₂/E₁ или с уве­личением перепада температур между участками отливки e_ус2 увеличивается и становится больше свободной усадка сплава. Так как модуль упругости по мере приближения к температуре солидуса резко увеличивается, примем E₂ << E₁. При этом

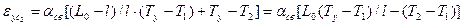
Из этого выражения видно, что, чем больше длина отливки Lo при заданной длине термического узла l, тем больше усадка в этом узле превышает свободную усадку сплава e_ус. На этом ос­новано применение пробы на горячеломкость сплавов А. Татюра (см. рис. 3.29, а). Очевидно, что, чем больше расстояние между утолщениями отливок пробы, тем больше e_ус в них и больше ве­роятность получения горячих трещин.

В общем виде, как предложено Г. Ф. Баландиным, относи­тельную усадку в отдельных частях отливки можно выразить формулой

e = me_у

где m ³ 1 — коэффициент, учитывающий неравномерность охлаж­дения частей отливки.

Горячие трещины возникают, когда при деформации me_у упру­гие напряжения превысят предел прочности сплава, т. е. при Eme_у ³ s_y. Таким образом, горячие трещины образуются чаще всего в термических, толстостенных частях отливки. В данном случае не соблюдается известная истина: где тонко, там и рвется. Для определения коэффициента т необходимо решить тепловую задачу затвердевания сплава (и расчета температурного поля отливки), совмещенную с приведенными выше реологическими уравнениями для расчета деформации сплава и развивающихся напряжений. При этом необходимо использовать экспериментальные данные по реологическим характеристикам сплава в зависи­мости от температуры.

Предел прочности сплава s_в является важнейшим реологиче­ским свойством. С повышением температуры s_в уменьшается.

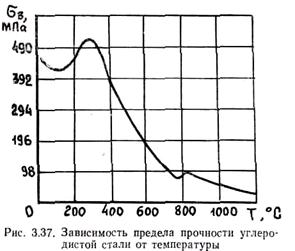
На рис. 3.37 приведен график зависимости s_в углеродистой стали от температуры. Видно, что увеличение температуры до 100 °С приводит к некоторому снижению s_в с последующим его повыше­нием примерно до 300 °С. Дальнейшее увеличение t приводит к рез­кому уменьшению s_в. Зону около 300 °С называют зоной сине­ломкости. При увеличении температуры стали до 1 100°С ее проч­ность уменьшается почти в 10 раз. Систематические и надежные данные по прочности стали в интервале кристаллизации в лите­ратуре отсутствуют. По данным Г. Ф. Баландина, прочность s_в алюминиевых сплавов в интервале кристаллизации изменяется в пределах 0,5 - 1 МПа.

Математическая модель образования горячих трещин для от­ливок простейших конфигураций при некоторых допущениях полу­чена Л. П. Каширцевым. Рассмотрение этой модели и ее реали­зацию на ЭВМ целесообразно осуществить на одном из практи­ческих занятий по курсу.

На основании изложенных выше теоретических положений рас­смотрим важнейшие мероприятия по предотвращению горячих трещин в отливках.

3.4.1.4. МЕРОПРИЯТИЯ ПО БОРЬБЕ С ОБРАЗОВАНИЕМ ГОРЯЧИХ ТРЕЩИН В ОТЛИВКАХ

Все мероприятия могут быть классифицированы по следующим направлениям: конструирование технологических отливок, управ­ление тепловым режимом их затвердевания, повышение податли­вости форм и стержней, повышение жесткости термических узлов отливки, повышение предела прочности сплавов и оптимизация их реологических свойств.

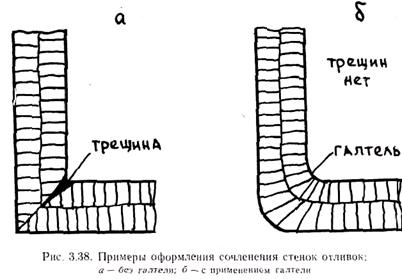
Очевидно, что идеальным было бы конструировать отливки с минимальными перепадами толщин стенок, без термических уз­лов, исключая затруднение усадки. Однако решение максималь­ной задачи нереально. Из изложенной выше теории следует, что нет необходимости устранять термические узлы и торможение усадки. Последнее вообще исключило бы применение металличе­ских форм и стержней. Целесообразно при конструировании от­ливок размещать термические узлы на расстояниях друг от друга L, не превышающих некоторых максимально допустимых значе­ний L_доп. Величину L_доп можно определить по технологическим пробам типа пробы А. Татюра. Если это невозможно из конструк­тивных соображений, то дополнительные тепловые узлы, преду­смотренные с целью уменьшения L, можно удалять последующей механической обработкой. В местах сочленения стенок необходи­мо предусматривать закругления — галтели. На рис. 3.38 приве­дена схема оформления сочленения стенок отливки. Без приме­нения галтелей в месте сочленения часто образуются горячие трещины, так как здесь расположен термический узел и при транскристаллизации в месте стыка столбчатых зон может образовать­ся плоскость слабины.

Более подробно рекомендации по конструированию отливок, а также вопросы улучшения податливости форм и стержней рас­сматриваются в технологических курсах.

Для управления охлаждением затвердевающих отливок приме­няются методы, рассмотренные в гл. 3.3 (внутренние и наружные холодильники, смеси различной теплоаккумулирующей способно­сти и т. п.).

Влияние различных способов управления охлаждением кри­сталлизующейся отливки на прочность стальных образцов с раз­ными термическими узлами показано на рис. 3.39.

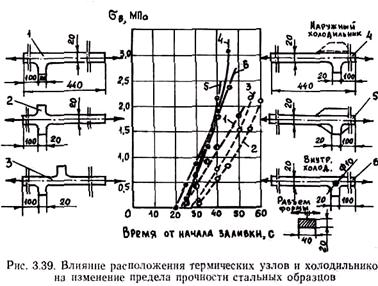
На образование горячих трещин оказывают влияние способ подвода сплава, продолжительность и температура его заливки. Очевидно, что сосредоточенный подвод сплава в термические уз­лы будет способствовать образованию горячих трещин. При этом вероятность их появления будет тем больше, чем выше темпера­тура заливки и больше ее продолжительность. Поэтому подвод сплава целесообразно осуществлять к тонкостенным частям от­ливки. При этом, чем выше температура заливки и медленнее она осуществляется, тем сильнее прогревается форма, оформляющая тонкостенную часть, меньше перепад температур и вероятность образования трещин. Если отливка имеет равномерную толщину стенки, подвод сплава необходимо осуществлять через несколько

распределенных по длине отливки питателей. В отливках простой конфигурации, склонных к образованию усадочных раковин, под­вод сплава целесообразно осуществлять под прибыль, в толсто­стенную часть.

Действенным средством предотвращения горячих трещин яв­ляется выполнение на термических узлах тонкостенных усадочных ребер. Ребра, затвердевая раньше узла, как бы армируют его и, благодаря большей прочности, препятствуют образованию тре­щин (рис. 3.40).

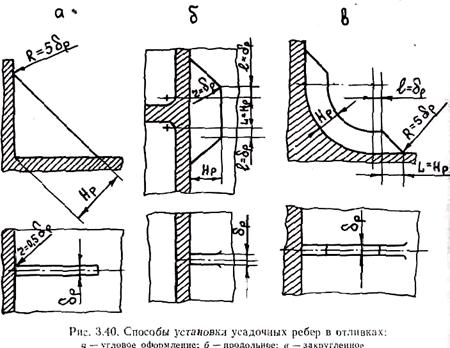
Размеры ребер выбирают по эмпирическим таблицам в зави­симости от толщины основной стенки отливки d₀. В первом при­ближении толщину ребра d_р можно принять равной d₀/3.

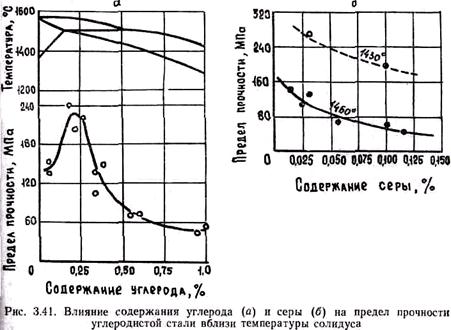
На образование горячих трещин оказывает влияние характер затвердевания сплава. При последовательном затвердевании об­разующаяся твердая корка увеличивает сопротивляемость раз­рушению. Поэтому последовательно затвердевающие сплавы менее склонны к образованию горячих трещин, чем объемно затверде­вающие. Образованию трещин способствуют ликвационные процес­сы, выделение хрупких интерметаллидов и неметаллических вклю­чений. Прочность сплавов в интервале кристаллизации существенно зависит от химического состава сплава (рис. 3.41). Видно, что даже сотые доли процента серы резко снижают прочность стали. Пониженной прочностью, а значит, и склонностью к горя­чим трещинам обладают как низкоуглеродистые (0,2% С), так и высокоуглеродистые стали.

Вопросы горячеломкости различных сплавов и методы воз­действия на нее рассматриваются в технологических курсах.

3.4.2. ЛИТЕЙНЫЕ НАПРЯЖЕНИЯ В ОТЛИВКАХ

После затвердевания отливки осуществляется ее охлаждение в форме, сопровождающееся фазовыми превращениями (напри­ мер превращением a ® g в железоуглеродистых сплавах, выде­лением избыточных фаз по линиям переменной растворимости в алюминиевых, магниевых и других сплавах) и дальнейшим развитием линейной усадки. Тепловая сторона охлаждения отлив­ки рассмотрена в курсе «Основы литейной гидравлики и теплофизики». Развитие линейной усадки и фазовых превращений в твердом состоянии приводит к формированию напряжений в от­ливке. Причиной напряжений является торможение линейной усад­ки и объемных изменений при фазовых превращениях.

Различают механическое и термическое торможение усадки.

Механическое торможение усадки осуществляется стержнями и выступающими частями формы (см. рис. 3.28). Возникающие при этом напряжения называют усадочными. Механическая картина формирования напряжений и деформаций при этом аналогична вышеописанной и принципиально может быть выражена рассмот­ренными уравнениями. Однако температурный интервал здесь гораздо шире интервала образования горячих трещин и охватывает охлаждение отливки от температуры солидуса до комнатной тем­пературы. При этом реологические свойства сплава изменяются в широких пределах. Прежде всего, начиная с температуры соли­дуса, резко увеличивается пластичность сплава, которая при даль­нейшем снижении температуры уменьшается. Суммарная деформа­ция сплава g является суммой упругой и пластической составля­ющих, а также деформации упругого последействия. При этом вблизи температуры солидуса превалирует пластическая дефор­мация и деформация упругого последействия. По мере уменьшения температуры увеличивается влияние упругой деформации, кото­рая является определяющей при низких температурах.

Известно, что пластическая деформация сопровождается де­формационным упрочнением, т. е. приводит к возникновению на­пряжений. Обычно эти напряжения так же, как в законе Гука, считают пропорциональными относительной деформации при зна­чительно меньших значениях коэффициента пропорциональности по сравнению с модулем упругости. При приближенном анализе формирования напряжений, начиная с основополагающих работ русского металлурга Н. В. Калакуцкого, весь температурный интервал разбивают на два участка: высокотемпературный, в ко­тором сплав проявляет только пластические свойства, и низко­температурный, в котором сплав представляет собой чисто упру­гое тело. При этом в пластической области отсутствует деформа­ционное упрочнение, т. е. при деформации не возникает никаких напряжений.

Разделяющую указанные участки температуру перехода из пластической зоны в упругую Т_п принимают равной 0,4¸0,5Т_сол. Для чугуна и стали, по предложению Н. Г. Гиршовича, принима­ют Т_п = 400¸500°'С. Очевидно, что такое представление является идеализированным, так как в зависимости от деформации и на­пряжений во всем интервале температур сосуществуют как пла­стические, так и упругие деформации. Однако, несмотря на это, указанное представление позволяет получить достоверные данные по формированию напряжений как на качественном, так и на количественном уровне. Строгое рассмотрение этого вопроса в на­стоящее время принципиально возможно, но сдерживается отсут­ствием систематических данных о реологических свойствах сплавов во всем интересующем нас температурном интервале.

3.4.2.1. УСАДОЧНЫЕ НАПРЯЖЕНИЯ В ОТЛИВКАХ

Вследствие механического торможения усадки стержнями или выступающими частями формы в отливке возникают растягиваю­щие деформации, равные, как было показано в предыдущем раз­деле, e = e_ус - e_п + e_р. При этом до температуры T = T_п деформа­ции носят пластический характер и напряжения не возникают. При Т < T_п деформации носят упругий характер, что приводит к формированию упругих растягивающих напряжений

s = E[e(T) - e(T_п)] = Ea_св[(T_c – T) – (T_c – T_п)] = Ea_св(T_п – T)

Отметим, что данное выражение справедливо при e_п = 0 и e_р = 0, т. е. для полностью неподатливой и не расширяющейся формы или стержня. Если все стенки отливки охлаждаются с оди­наковой скоростью и в момент выбивки имеют одинаковую тем­пературу, то усадочные напряжения будут иметь временный, об­ратимый характер. При выбивке отливки из формы и удалении стержней, т. е. при устранении нагрузки, они полностью снима­ются. Однако если в момент выбивки температура отдельных уз­лов отливки различна, то после выбивки в ней возникают оста­точные напряжения.

Пусть конструкция отливки содержит тонкую и толстую стен­ки, жестко связанные друг с другом. Если в момент выбивки температура тонкой части Т₁ будет меньше температуры толстой части Т₂, то упругие напряжения растяжения в них будут разные. В тонкой части напряжение равно s₁ = a_св(T_п – Т₁), а в тол­стой — s₂ = a_свE(T_п – Т₂). Так как Т₁ < Т₂, то s₁ > s₂. После вы­бивки отливка сократится на величину la_св(T_п – Т₂), т. е. в тол­стой части деформация исчезнет. В тонкой же части при этом останется относительная деформация a_св(T_п – Т₁), поскольку ее снятие связано со сжатием толстой части. Так как тонкая часть стремится к сокращению, в отливке сохранятся остаточные на­пряжения. При этом в тонкой части будут растягивающие, а в толстой—сжимающие напряжения. Деформация в тонкой части несколько уменьшится, а в толстой части появится сжимающая деформация, равная этому уменьшению, т. е. e₁ + e₂ = a_св(T_п – Т₁), где e₁ и e₂ — относительные деформации в тонкой и тол­стой частях. Исходя из условий равновесия, можно записать уравнение Ee₁S₁ = Ee₂S₂, где S₁ и S₂ — площади сечений тонкой и толстой стенок отливки. Из этого уравнения получаем выражения для остаточных напряжений в стенках:

; .

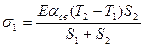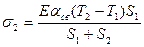Очевидно, что величина этих напряжений тем больше, чем больше разность температур узлов отливки в момент выбивки.

С этим необходимо считаться, определяя момент ее выбивки. Этот вопрос нельзя решить однозначно. С точки зрения уменьшения усадочных напряжений целесообразно применять раннюю выбив­ку. Если выбить отливку из формы и удалить стержни в момент, пока тонкостенные части не перешли в упругое состояние, то уса­дочные напряжения не возникнут. Однако вследствие более быст­рого охлаждения отливки на воздухе в ней могут возникнуть термические напряжения, вызванные термическим торможением усадки. Поэтому отливки, склонные к значительным термическим напряжениям, после ранней выбивки помещают в печи и охлаж­дают вместе с ней.

3.4.2.2. ТЕРМИЧЕСКИЕ НАПРЯЖЕНИЯ В ОТЛИВКАХ

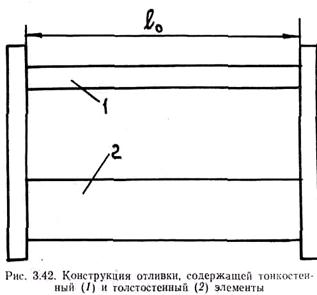
Термическое торможение усадки возникает вследствие не­равномерного ее развития в различных элементах отливки. Рас­смотрим тонкостенный и толстостенный стержни, жестко связан­ные друг с другом (рис. 3.42). В начальный момент времени оба стержня имеют температуру Т₀ > Т_п. Конструкция охлаждается до достижения обоими стержнями одинаковой температуры T_к. Очевидно, что тонкостенный элемент будет остывать быстрее, чем толстостенный. Соответственно быстрее будет развиваться и его

усадка. На рис. 3.43 приведены кривые изменения температуры и длины обоих стержней.

Если бы стержни не были связаны друг с другом, то их дли­ны уменьшались бы в строгом соответствии с температурными кривыми: l₁ = l₁[1 - a_св(T₀ – Т₁(t))] и l₂ = l₀[1 - a_св(T_п – Т₂(t))].

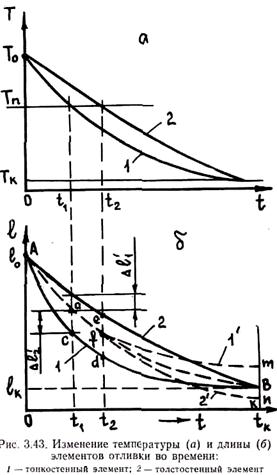
Однако так как они связаны друг с другом, то в каждый момент они имеют одинаковую длину, изменение которой характеризует штриховая линия на рис. 3.43. Рассмотрим сначала качественную картину формирования напряжений, а затем дадим количествен­ную оценку. В момент времени t₁ из пластического в упругое со­стояние переходит тонкий стержень; толстый стержень достигает температуры T_п в момент t₂. Рассмотрим поведение системы в следующие моменты времени: (0 ¸ t₁), (t₁ ¸ t₂), (t₂ ¸ t_к).

При t < t₁ оба стержня находятся в пластическом состоянии. При этом тонкий стержень пластически растянут, а толстый стержень сжат. В момент t₁ эти деформации равны ∆l₁ и ∆l₂. Напряжения в системе отсутствуют. При t₁ < t < t₂ тонкий стер­жень находится в упругом состоянии, а толстый — в пластическом. Так как тонкий стержень деформируется упруго, в этом времен­ном интервале кривая изменения длины отливки параллельна кривой изменения длины тонкого стержня, если бы он охлаждался отдельно от толстого, т. е. af\\cd и ac=fd (напряжения в системе при этом отсутствуют).

В момент t = t₂ толстый стержень переходит в упругое состоя­ние. При этом тонкий стержень упруго растянут на величину отрезка fd, а толстый — пластически сжат на величину ef. В даль­нейшем оба стержня будут вести себя как упругие тела. Поэтому если при t = t₂ стержни разъединить друг от друга, то изменение их длины будет развиваться по кривым, параллельным соответ­ствующим кривым изменения длины несвязанных стержней. Дли­на первого стержня изменяется по кривой fm\\dB, а второго — по кривой fn\\eB.

При достижении температуры T_к при t = t_к. разделенные стержни имели бы длины, соответственно равные отрезкам km и kn Фактическая же длина связанных стержней в этот момент равна kB. Очевидно, что после полного охлаждения отливки и выравнивания температур составляющих ее стержней толстый стержень будет растянут на величину отрезка пВ, а тонкий — сжат на величину отрезка Вт, причем Bm = fd и nB = ef, т. е. остаточные деформации равны по величине и обратные по знаку деформациям, которые имели стержни в момент перехода толстого стержня из пластического, состояния в упругое. Таким образом, в тонких эле­ментах будут развиваться остаточные напряжения сжатия, а в толстых — растяжения. В данном случае природа как бы «сжали­лась» над чугунолитейщиками. Известно, что чугун имеет доста­точно высокую прочность на сжатие и низкую прочность при рас­тяжении. Если бы характер остаточных напряжений был бы про­тивоположным, то качественные чугунные отливки получить было бы невозможно.

С целью упрощения количественного анализа процесса при­мем, что стержни остывают в условиях конвективной теплопере­дачи. Напишем уравнение теплового баланса стержня. За время dt от стержня в форму будет отведено количество тепла, равное dQ = a×F(T— T_ф)dt. При этом температура стержня уменьшится на dT и его теплосодержание изменится на dH = CrVdT, где V — объем стержня. Так как dH = -dQ, CrVdT = -aF(T—T_к)dt. Интегрируя это уравнение при начальном условии (t = 0, Т = Т₀) получаем формулу для изменения температуры стержня:

Дата добавления: 2014-12-16