Дифференциальные уравнения движения механической системы

Рассмотрим механическую систему, состоящую из материальных точек. Для каждой точки системы в инерциальной системе отсчета справедлив второй закон Ньютона:

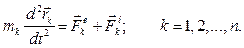(3.1)

где

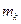– масса точки с номером ;

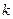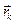– ее радиус–вектор;

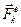– равнодействующая всех внешних сил как активных, так и реакций связей, действующих на точку с номером ;

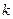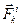– равнодействующая всех внутренних сил, действующих на точку с номером .

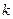Систему уравнений (3.1) называют системой дифференциальных уравнений движения точек механической системы. Одна из основных задач механики состоит в том, чтобы, зная активные силы и связи, наложенные на систему, определить движение всех точек системы и определить реакции связей. Решение такой задачи связано с интегрированием системы уравнений (3.1) при заданных начальных условиях. Однако, прямое интегрирование системы (3.1) весьма сложно, что связано как с возможно большим числом этих уравнений, так и, в основном, с неопределенностью информации о внутренних силах.

Во многих практически интересных случаях нет необходимости определять все интегралы системы (3.1), достаточно получить лишь некоторые из них. Это позволяют сделать общие теоремы динамики. Являясь прямым следствием уравнений (3.1), общие теоремы динамики связывают основные динамические величины, характеризующие движение системы, с приложенными к ней внешними силами.

Дата добавления: 2014-12-16