Теорема об изменении кинетического момента

Производная по времени от количества движения механической системы равна геометрической сумме всех приложенных к системе внешних сил.

Теорема об изменении количества движения механической системы

Сложим почленно все равенства (3.1):

Учитывая первое основное свойство внутренних сил (3.2), получаем:

(3.4)

Преобразуем левую часть равенства (3.4). Учитывая, что масса точки считается постоянной и что получаем:

Произведение массы точки на вектор ее скорости называется количеством движения материальной точки.

Количеством движения механической системы называется сумма количеств движения всех ее точек:

(3.5)

Равенство (3.4) принимает вид:

(3.6)

Доказана теорема об изменении количества движения механической системы:

Умножим каждое из уравнений (3.1) слева векторно на радиус–вектор соответствующей точки

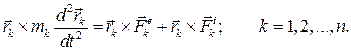
и сложим все полученные уравнения:

Учитывая второе основное свойство внутренних сил (3.3), получаем:

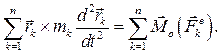(3.7)

Вектор 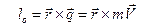называется моментом количества движения материальной точки относительно центра .

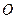Заметим, что техника вычисления момента количества движения относительно центра или оси такая же, как техника вычисления момента силы относительно центра или оси.

Сумма моментов количеств движения всех точек механической системы относительно центра 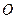называется моментом количества движения или кинетическим моментом механической системы относительно центра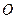

Вычислим производную по времени от кинетического момента:

Первое слагаемое в квадратной скобке равно нулю, так как векторно перемножаются два коллинеарных вектора. Таким образом,

Сравнивая последний результат с левой частью равенства (3.7), получаем:

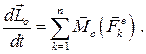(3.8)

Доказана теорема об изменении кинетического момента механической системы:

Дата добавления: 2014-12-16