Принцип возможных перемещений. Принцип возможных перемещений устанавливает условия равновесия механических систем

ЛЕКЦИЯ 8

Принцип возможных перемещений устанавливает условия равновесия механических систем. Под равновесием механической системы традиционно понимают состояние ее покоя по отношению к выбранной инерциальной системе отсчета.

Рассмотрим механическую систему, состоящую из материальных точек. Для ее равновесия необходимо и достаточно, чтобы суммы всех сил, действующих на каждую точку системы, и скорости всех точек в начальный момент времени равнялись нулю:

(8.1)

где 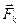– равнодействующая всех активных сил, действующих на точку с номером ;

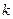– равнодействующая всех сил реакций связей, наложенных на точку с номером .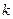

Для равновесия механической системы с идеальными удерживающими стационарными связями необходимо и достаточно, чтобы сумма элементарных работ всех приложенных к системе активных сил на любом возможном перемещении системы равнялась нулю и скорости всех точек в начальный момент времени равнялись нулю:

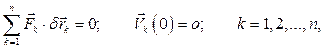(8.2)

Сформулированное утверждение называют принципом возможных перемещений. Необходимость. Пусть механическая система находится в равновесии. Следовательно, выполняются условия (8.1). Из данного положения дадим системе возможное перемещение. Умножим каждое из уравнений (8.1) скалярно на соответствующее точке возможное перемещение и сложим все полученные уравнения:

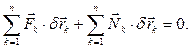(8.3)

По условию связи идеальные, следовательно, справедливо равенство (7.1). Из (8.6) и (8.3) получаем (8.2).

Достаточность. Приложим к точкам покоящейся механической системы систему сил, удовлетворяющих равенству (8.2) и, следовательно, поскольку связи идеальные (7.1), равенству

(8.4)

Покажем, что механическая система останется в покое. Допустим противное – система под действием приложенных сил пришла в движение, т.е. ее точки получили ускорения 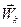. Эти ускорения должны быть направлены по касательным к траекториям точек, поскольку скорости равны нулю и нормальные составляющие ускорений отсутствуют. Таким образом, действительные перемещения точек пропорциональны их ускорениям. По условию связи стационарные и, следовательно, среди возможных перемещений системы найдется такое, которое совпадает с действительным. Возьмем в качестве возможного перемещения систему векторов, пропорциональных ускорениям точек 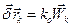. Равенство (8.4) примет вид: или, учитывая, что для каждой точки справедлив второй закон Ньютона,

Это равенство может иметь место только в том случае, если ускорения всех точек равны нулю Следовательно, механическая система после приложения активных сил останется в покое.

Заметим, что если вместо возможных перемещений использовать пропорциональные им возможные скорости (что позволяет в полной мере использовать при решении задач кинематические методы), то условия равновесия записываются в виде:

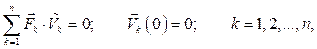(8.5)

т.е.

Дата добавления: 2014-12-16