Общее уравнение динамики

Пример 2

Полиспаст состоит из неподвижного блока и подвижных блоков (Рис.8.2). Определить в случае равновесия отношение веса 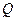поднимаемого груза 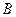к величине силы , приложенной к свободному концу 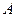троса.

Рис.8.2

Условие равновесия (8.5) имеет вид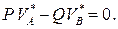

Рассмотрим первый из подвижных блоков. Точка 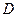– мгновенный центр скоростей блока. Возможная скорость точки 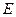численно равна возможной скорости точки 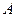. Следовательно, Скорость центра каждого последующего подвижного блока равна половине скорости центра предыдущего подвижного блока. Таким образом,

Подставляя полученный результат в условие равновесия, имеем:

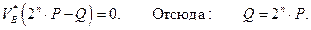
Рассмотрим механическую систему, состоящую из материальных точек, на которую наложены идеальные удерживающие связи. Уравнения движения точек имеют вид:

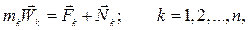
где

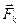– равнодействующая всех активных сил, действующих на точку с номером ;

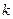– равнодействующая реакций связей, наложенных на точку с номером .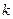

При фиксированном времени дадим точкам системы возможные перемещения. Умножим каждое из уравнений движения скалярно на соответствующее возможное перемещение и сложим все полученные уравнения:

Поскольку по условию связи идеальные (7.1), последняя сумма равна нулю и, следовательно,

(8.6)

Уравнение (8.6) называется общим уравнением динамики.

При использовании общего уравнения динамики удобно вводить в рассмотрение силы инерции. В этом случае уравнение (8.6) принимает вид:

(8.7)

Равенство (8.7) составляет содержание так называемого принципа Лагранжа–Даламбера:

Дата добавления: 2014-12-16