Глобальная интерполяция

В случае глобальной интерполяции отыскивается единый полином на всем интервале [ a, b ], т.е. строится полином, который используется для интерполяции функции f(x) на всем интервале изменения аргумента x. Будем искать интерполирующую функцию в виде полинома (многочлена) m –ой степени P_m (x) =a ₀ +a ₁ x+a ₂ x ² +a ₃ x ³ +…+a_m x^m. Какова должна быть степень многочлена, чтобы удовлетворить всем условиям интерполяции? Допустим, что заданы две точки: (x ₀, f ₀) и (x ₁, f ₁), т.е. N=1. Через эти точки можно провести единственную прямую, т.е. интерполирующей функцией будет полином первой степени P ₁(x) =a ₀ +a ₁ x. Через три точки (N=2) можно провести параболу P ₂(x) =a ₀ +a ₁ x+a ₂ x ² и т.д. Рассуждая таким способом, можно предположить, что искомый полином должен иметь степень N.

Для того, чтобы доказать это, выпишем систему уравнений на коэффициенты. Уравнения системы представляют собой условия интерполяции в при каждом x=x_i:

Данная система является линейной относительно искомых коэффициентов a ₀, a ₁, a ₂, …, a_N. Известно, что СЛАУ имеет решение, если ее определитель отличен от нуля. Определитель данной системы

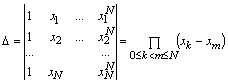
носит имя определителя Вандермонда. Из курса математического анализа известно, что он отличен от нуля, если x_k ≠ x_m (т.е. все узлы интерполяции различные). Таким образом, доказано, что система имеет решение.

Мы показали, что для нахождения коэффициентов
a ₀, a ₁, a ₂, …, a_N надо решить СЛАУ, что является сложной задачей. Но есть другой способ построения полинома N –й степени, который не требует решения такой системы.

Дата добавления: 2014-12-16