
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Метод прямоугольников
|
|
|
|
Простейшим методом численного интегрирования является метод прямоугольников. Он непосредственно использует замену определенного интеграла интегральной суммой:
 . .
| (7.3) |
Разобьём интервал интегрирования [ a, b ] на n равных частей. Обозначим  хi = h шаг разбиения. Формула прямоугольника применяется к каждому отрезку. В качестве точек
хi = h шаг разбиения. Формула прямоугольника применяется к каждому отрезку. В качестве точек 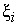 выбираются левые
выбираются левые 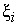 = хi -1) или правые (
= хi -1) или правые (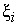 = хi) границы элементарных отрезков (рис.7.1).
= хi) границы элементарных отрезков (рис.7.1).
Соответственно, для этих двух случаев можно записать формулы метода прямоугольников:
 ; ;
| (7.4) |
 . .
| (7.5) |
Более точным является вид формулы прямоугольников, использующий значения функции в средних точках элементарных отрезков: точка 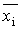 . Таким образом, площадь криволинейной трапеции заменяется суммой прямоугольников с основанием h и высотами, равными значениям функции f (x) в середине оснований
. Таким образом, площадь криволинейной трапеции заменяется суммой прямоугольников с основанием h и высотами, равными значениям функции f (x) в середине оснований 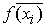 (рис.7.2).
(рис.7.2).
Получим формулу:
 , где , где 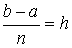 , ,
| (7.6) |
или
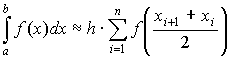 . .
| (7.7) |
На рис.7.3. приведена блок- - схема метода прямоугольников, в Приложении - программа с графическим выводом интегральной кривой.
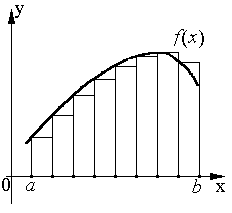
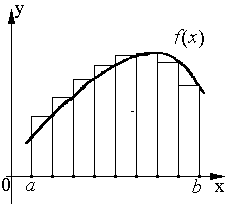

Рис.7.1

Рис.7.2

Рис.7.3. Блок-схема метода прямоугольников
Метод трапеций
Метод трапеций использует линейную интерполяцию, т.е. график функции у = f (х) представляется в виде ломаной, соединяющей точки (хi, уi). В этом случае площадь всей криволинейной трапеции складывается из площадей элементарных прямоугольных трапеций (рис.7.4 а, 7.4 б)
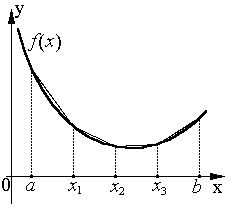
Рис.7.4 а
Рис.7.4 б
Площадь каждой такой трапеции определяется по формуле:
 , i=1,2,...,n. , i=1,2,...,n.
| (7.8) |
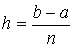 , где n - число интервалов разбиения.
, где n - число интервалов разбиения.
Складывая все эти равенства, получим формулу трапеций для численного интегрирования:
 , ,
| (7.9) |
или
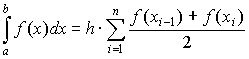 . .
| (7.10) |
Формулы (7.9) и (7.10) можно представить в виде:
 , ,
| (7.11) |
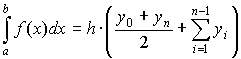 . .
| (7.12) |
Блок - схема алгоритма метода трапеций приведена на рис.7.5.
Метод парабол (формула Симпсона)
Этот метод более точный по сравнению с методами прямоугольников и трапеций.
В основе формулы Симпсона лежит квадратичная интерполяция подынтегральной функции на отрезке [a,b] по трем равноотстоящим узлам.
Разобьем интервал интегрирования [a, b] на четное число n равных отрезков с шагом h.
Примем: x 0= a, x 1= x 0+ h,..., x n = x 0+ nh = b.
Значения функций в точках обозначим соответственно:
y 0= f (a); y 1= f (x 1); y 2= f (x 2);...; yn = f (b).

Рис. 7.5. Блок-схема метода трапеций
На каждом отрезке [ x 0, x 2], [ x 2, x 4],..., [ xi -1, xi +1] подынтегральную функцию f (x) заменим интерполяционным многочленом второй степени.
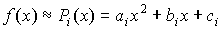 , где , где  . .
| (7.13) |
В качестве Рi (х) можно принять интерполяционный многочлен Лагранжа второй степени, проходящий через концы каждых трех ординат:
| y 0, y 1, y 2; y 2, y 3, y 4; y 4, y 5, y 6;....; yn -2, yn -1, yn. |
Формула Лагранжа для интервала [ xi -1, xi +1]:

|

Рис. 7.6.
Элементарная площадь si (рис.7.6) может быть вычислена с помощью определенного интеграла. Учитывая, что xi - xi -1= xi +1- xi = h и, проведя вычисления, получим для каждого элементарного участка:
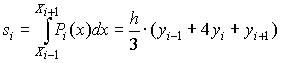 . .
| (7.14) |
После суммирования интегралов по всем отрезкам, получим составную формулу Симпсона:
 . .
| (7.15) |
Часто пользуются простой формулой Симпсона:
 . .
| (7.16) |

Рис.7.7. Блок-схема метода Симпсона
Пример 7.1. Вычислить интеграл
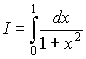 . .
|
Разбиваем интервал интегрирования на 10 равных частей: n =10. Шаг интегрирования h = (1-0)/10=0.1. Результаты вычислений подынтегральной функции приведены в табл. 7.1.
Таблица 7.1
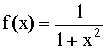
| |||||
| xi | xi 2 | 1+ xi 2 | f (xi) i =1,3,... | f (xi) i =2,4,... | f (x 0), f (x 10) |
| 0.0 | 0.00 | 1.00 | -- | -- | 1.00000 |
| 0.1 | 0.01 | 1.01 | -- | -- | |
| 0.2 | 0.04 | 1.04 | -- | 0.96154 | -- |
| 0.3 | 0.09 | 1.09 | 0.91743 | -- | -- |
| 0.4 | 0.16 | 1.16 | -- | 0.76207 | -- |
| 0.5 | 0.25 | 1.25 | 0.70000 | -- | -- |
| 0.6 | 0.36 | 1.36 | -- | 0.073529 | -- |
| 0.7 | 0.49 | 1.49 | 0.67114 | -- | -- |
| 0.7 | 0.64 | 1.64 | -- | 0.60976 | -- |
| 0.9 | 0.71 | 1.71 | 0.55249 | -- | -- |
| 1.0 | 1.00 | 2.00 | -- | -- | 0.50000 |

| 3.93116 | 3.16766 | 1.50000 |
Вычислим интеграл по формуле трапеций (7.12):

по формуле Симпсона (7.15):
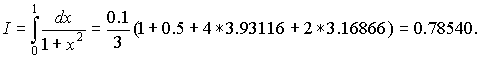
Для вычисления интеграла по методу прямоугольников, необходимо вычислить значения функции в середине каждого элементарного отрезка: 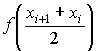 или
или  . Результаты вычислений подынтегральной функции приведены в табл. 7.2.
. Результаты вычислений подынтегральной функции приведены в табл. 7.2.
Таблица 7.2
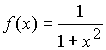
| |||
| xi | 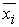
| 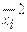
| 
|
| 0.0 | 0.05 | 0.0025 | 0.9975 |
| 0.1 | 0.15 | 0.0225 | 0.9770 |
| 0.2 | 0.25 | 0.0625 | 0.9412 |
| 0.3 | 0.35 | 0.1225 | 0.7907 |
| 0.4 | 0.45 | 0.2025 | 0.7316 |
| 0.5 | 0.55 | 0.3025 | 0.7677 |
| 0.6 | 0.65 | 0.4225 | 0.7030 |
| 0.7 | 0.75 | 0.5625 | 0.6400 |
| 0.7 | 0.75 | 0.7225 | 0.5705 |
| 0.9 | 0.95 | 0.9025 | 0.5256 |
| 1.0 | 1.00 | 1.00 | -- |

| 7.756 |
По формуле прямоугольников (7.6) получим:

|
Найдем точное значение интеграла:
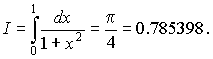
|
Относительная погрешность при применении формулы трапеций составляет 0,05 %, формулы прямоугольников - 0,026 %, формулы Симпсона - 0,00025 %. Таким образом, точность вычислений по формуле Симпсона выше, чем по формулам трапеций и прямоугольников.
Пример 7.2. Вычислить значение энтропии воды при нагревании ее от 400 до 500 К по формуле:
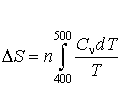
 .
.
Принимаем количество молей n =1, значение теплоемкости при v =const:
Cv=35.0 Дж/моль*К.
Разобьем интервал интегрирования на 10 равных частей. Шаг интегрирования будет равен h =(500 - 400) /10 =10.
Результаты вычислений подынтегральной функции поместим в табл. 7.3.
Вычислим интеграл, используя данные табл.7.3:
по формуле трапеций (7.12):
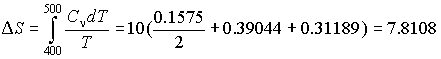 ,
,
по формуле Симпсона (7.15):
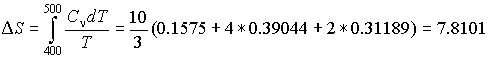 ,
,
Таблица 7.3

| |||||
| Т | f (Ti) i= 1,3, … | f (Ti) i =2,4, … | f (T 0) f (T 10) | 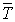
| 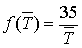
|
| - | 0.0875 | 0.08642 | |||
| 0.08536 | 0.08434 | ||||
| 0.08333 | 0.08235 | ||||
| 0.08140 | 0.08046 | ||||
| 0.07955 | 0.07865 | ||||
| 0.07778 | 0.07692 | ||||
| 0.07609 | 0.07527 | ||||
| 0.07447 | 0.07368 | ||||
| 0.07292 | 0.07216 | ||||
| 0.07143 | 0.07071 | ||||
| 0.0700 | |||||

| 0.39044 | 0.31189 | 0.1575 | 0.78096 |
по формуле прямоугольников (7.6):
 .
.
Найдем точное значение интеграла:
 .
.
Относительная погрешность вычислений по формуле трапеций, Симпсона и прямоугольников составляет соответственно: 0.01 %, 0.001 %, 0.005 %. Таким образом, наибольшую точность вычислений получили по формуле Симпсона.
|
|
|
|
|
Дата добавления: 2014-12-16; Просмотров: 2147; Нарушение авторских прав?; Мы поможем в написании вашей работы!