Пример 6.2

Способы нахождения обратных чисел

Нахождение обратных величин

Если задано уравнение , то величина называется обратной величиной по модулю .

Обратная величина существует, если и – взаимно простые числа.

1. Перебором возможных значений.

Подставляя вместо 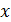числа: – добиваемся выполнения исходного уравнения.

Пример 6.1. 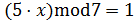, , т.к. .

2. С помощью функции Эйлера .

.

.

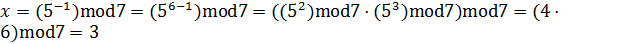3. С помощью алгоритма Евклида.

Алгоритм Евклида применяется для нахождения НОД чисел и 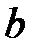. Однако его расширенный вариант можно использовать и для вычисления обратной величины.

Основной вариант.

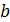Даны и , . Алгоритм имеет итерационный характер:

, ;

, ;

, ;

, ;

, ;

,

где , ‑ частное и остаток на ‑м шаге алгоритма. На первом шаге делимое ‑ , делитель ‑ 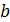, частное ‑ 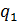, остаток ‑ . На ‑м, шаге алгоритма: делимое ‑ делитель ‑го шага, делитель ‑ остаток ‑го шага (), частное ‑ , остаток ‑ .

Пример 6.3. Пусть и . Найти .

То есть на четвертом шаге остаток от деления , следовательно, алгоритм останавливается и .

Доказано, что при неотрицательных и 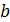можно найти такие целые числа: , , , что будет выполняться

.

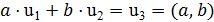Если выбрать и ‑ взаимно простые числа, т.е. , тогда

,

,

.

То есть для нахождения обратной величины необходимо вычислить . Эта задача решается в ходе вычисления в соответствии с алгоритмом Евклида. Дополнительно на каждом шаге вычисляются координаты двух векторов:

, .

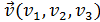Алгоритм вычисления имеет следующий вид

1. Начальные установки:

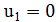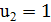, т.е. , , . При этом , т.е. ,

, т.е. , , . При этом .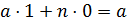

2. Проверяем, выполняется ли , если да, то алгоритм заканчивается.

3. Делим 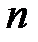на ( на ) и определяем:

и значения векторов: ; .

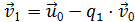4. Вернуться к шагу 2.

На каждом шаге при расчетах используются результаты предыдущего:

, , .

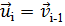При вычисления заканчиваются , где значение , полученное на последнем шаге.

Пример 6.4. Пусть и . Найти число 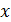, обратное числу по модулю 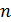, т.е. найти .

Используя расширенный алгоритм Евклида, выполним вычисления.

-
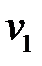
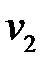
				-4
	-4				-1
		-1		-9
-	-9

При 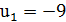, , выполняется уравнение , и . Итак, .

5.4. Криптосистема

Последовательность действий абонентов криптосистемы

Действия получателя криптограммы В:

1. В генерирует два произвольных больших простых числа 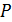и 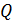. Эти числа должны быть примерно одинаковыми, размерностью 100‑150 десятичных разрядов. Они должны быть секретными.

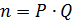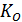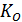2. В вычисляет значение модуля и функции Эйлера и выбирает значение открытого ключа с соблюдением условий: , =1, т.е. и 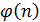должны быть взаимно простыми.

3. В вычисляет значение секретного ключа 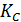, используя расширенный алгоритм Евклида:

.

4. В посылает А пару чисел по открытому каналу.

Действия отправителя криптограммы А:

1. Разбивает исходный текст на блоки , , т.е. . Величина .

2. Шифрует каждое число 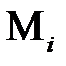по формуле =( и отправляет криптограмму .

Получатель В, получив криптограмму, расшифровывает каждый блок секретным ключом 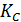, , и восстанавливает весь текст .

Реализуемость и безопасность

Покажем, что при расшифровании восстанавливается исходный текст. Согласно обобщению Эйлером малой теоремы Ферма: если , то , или . Открытый 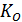и закрытый 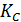ключи в алгоритме связаны соотношением 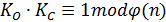, или для некоторого целого . Таким образом, процесс шифрования, а затем расшифрования некоторого сообщения 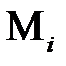выглядит следующим образом:

В процессе применения RSA злоумышленник может иметь: , , 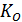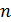– и организовать дешифрование двумя способами:

1. По , , 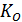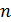получить . Для этого он решает задачу вычисления из уравнения 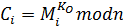. Эта задача вычислительно трудна.

2. По 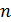вычислить 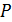и 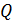, затем найти 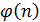и вычислить 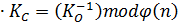и дешифровать сообщение .

Однако задача разложения большого числа на простые множители вычислительно сложна.

Пользователи А и В должны быстро осуществлять все вычисления: вычислять 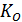, шифровать и расшифровывать.

Вычисление 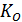с использованием алгоритма Евклида ‑ довольно быстрый процесс и не представляет трудности. Шифрование и расшифрование ‑ возведение большого числа в большую степень ‑ требует определенных затрат времени, но, с учетом наличия быстрых алгоритмов и быстродействия современных компьютеров, это приемлемая процедура.

Дата добавления: 2014-12-16