Решение задачи 2.3

Решение задачи 2.2

Точечная оценка СКО результата серии измерений определяется по формуле:

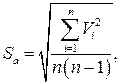
где V_i – отклонение отдельных измерений от математического ожидания серии из n измерений.

№ наблюдения	Результат наблюдения; li, мм	Отклонение наблюдения от математического ожидания; Vi, мм	Квадрат отклонения наблюдения от мате–матического ожидания; Vi^2, 10^–6мм^2
	18,309	0,001
	18,307	0,001
	18,312	0,004
	18,309	0,001
	18,304	0,004
	18,306	0,002
	18,309	0,001
	18,313	0,005
	18,308	0,000
	18,303	0,005
Σ	183,08

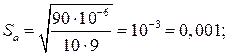
Точечная оценка СКО длины стержня 0,001 мм.

Задача 2.3

Результаты многократного измерения длины стержня (мм) следующие:

18,309	18,312	18,304	18,309	18,308
18,307	18,309	18,306	18,313	18,303

Построить гистограмму распределения.

Для отображения n полученных показаний СИ в виде гистограммы область численных значений между наименьшим и наибольшим показаниями (размах) R = L_max – L_min делят на интервалы одинаковой ширины ΔL и определяют число показаний n_k, попавших в каждый из полученных интервалов. Полученные результаты изображают графически, откладывая по оси абсцисс полученные максимальное и минимальное показания с обозначением границ интервалов между ними, а по оси ординат – величину n_k /(n ΔL). Построив над каждым из интервалов прямоугольники, основанием которых является ширина интервалов, а высотой – n_k /(n ΔL), получим гистограмму, дающую представление о плотности распределения вероятности полученных показаний в данном эксперименте. Относительную частоту попаданий n_k / n можно условно приравнять к вероятности попадания в конкретный интервал, а высоту прямоугольника считать равной эмпирической плотности вероятности р _k = n_k /(n ΔL).

Диапазон	Кол–во результатов
18,305 – 18,305]
(18,305 – 18,307]
(18,307 – 18,309]
(18,309 – 18,311]
(18,311 – 18,313

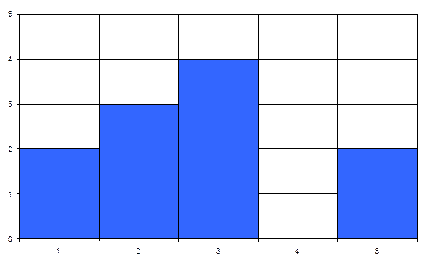
Гистограмма распределения

Задача 2.4

Результаты многократного измерения длины стержня (мм) следующие:

18,309	18,312	18,304	18,309	18,308
18,307	18,309	18,306	18,313	18,303

Построить полигон распределения.

Дата добавления: 2014-12-16