Теорема Бернулли. Закон больших чисел в форме Бернулли и его значение

Следует закон больших чисел

Теорема Чебышева. Закон больших чисел в форме Чебышева и его значение.

Если случайные величины Хi, i=1,2…,n,

независимы и одинак. распределены со

средними МХi =a и дисперсиями DXi =DX,

то справедлива теорема Чебышева:

n

P(|1/n сумма (Xi) - a | <= e) >= 1- DX/ne*e

i=1

Из этого неравенства при n стр-ся к беск-ти

n

limP(|1/n сумма (Xi)- a| <=e)=1

n-& i=1

Смысл закона закл. в том, что средние значения

случайных величин стремятся к их мат. ожиданию

при n- & по вероятн. Отклонение средн. значений

от мат.ожидания стан-ся сколь угодно малым с

вероятностью, близкой к 1, если n достаточно

велико или вероятность любого откл. средн. знач.

от а сколь угодно мала с ростом n.

(e – это эпсилон.)

Теорема Бернулли:

Если вер-ть наст-я соб-я А в каж-м из n повторных нез-х испыт-й пост-на, то при неогран-м увел-ии числа n исп-й отн-я частота наст-я соб-я А стрем-ся по вер-ти к числу p, т.е. для 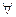>0

Т-ма Б-ли явл-ся теор-ким обосн-ем для стат-го опр-я вер-ти.

Неравенство Бернулли:

Пусть 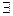n исп-й Бернулли с вер-ю успеха p, q=1-p и m – число успехов. Тогда для >0

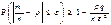
Пусть производится последовательность независимых испытаний, в результате каждого из которых может наступить или не наступить событие А, причем вероятность наступления этого события одна и та же при каждом испытании и равна р. Если событие А фактически произошло m раз в n испытаниях, то отношение m/n называют, как мы знаем, частотой появления события А. Частота есть случайная величина, причем вероятность того, что частота принимает значение m/n, выражается по формуле Бернулли (13):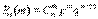
Закон больших чисел в форме Бернулли состоит в следующем: с вероятностью, сколь угодно близкой к единице, можно утверждать, что при достаточно большом числе опытов частота появления события А как угодно мало отличается от его вероятности, т. е.

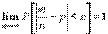
(55)

иными словами, при неограниченном увеличении числа n опытов частота m/n события А сходится по вероятности к Р(А). (Доказательство)

Мы говорили (см. § 1, п. 1), что при большом числе испытаний частота Р*(А)=m/n события А обладает свойством устойчивости. Это обстоятельство находит свое объяснение в законе больших чисел Бернулли.

Дата добавления: 2014-12-16