
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Использование преобразования Лапласа 2 страница
|
|
|
|
даточной функции.(Диф. уравнение преобразует-
ся по Лапласу). Передаточная функция записы-
вается для удобства в комплексном виде, на
мнимой оси p=jw можно найти АЧХ и ФЧХ линей-
ной системы. Передаточная функция дает инфор-
мацию об устойчивости системы.
3) Нелинейные динамические системы описываются
нелинейными диф. уравнениями, в этих системах
обязательно есть нелинейность вида (
и др.), общих решений и анализа через переда-
точную функцию как правило не существует, по-
этому есть два метода:
а) численный метод (Эйлера и др.) (восстановле-
ние по точкам)
б) решение диф. уравнений методом фазового порт-
рета (качественная теория). (Это наглядный
путь выяснения поведения нелинейной системы)
Стохастические системы
Стохастика - случайность.
Определение: Динамическая система называется стохастичес-
кой, если она описывается дифференциальным
или разностным уравнением, в правую часть
которого входит случайный процесс.
Такую систему можно представить в виде линейного или не-
линейного четырехполюсника, на вход которого подается шум
Стохастическая
x(t) система X(t)
x(t)- шум
X(t)- выходной процесс
Составление модели любой динамической системы должно
в реальных условиях(например движение самолета или раке-
ты) составляться с помощью предварительных экспериментов
над движением реальной системы. (Как правило это диффе-
ренциальные или разностные уравнения) и в эти уравнения
вставляется некоторый шум, который является случайным
процессом.
Для дальнейшего составления модели используется иден-
тификация модели на основании эксперимента или экспери-
ментальных данных.
Идентификацией называется оценка коэффициентов разност-
ного уравнения и оценка параметров шума:
дисперсии, мат. ожидания, ковариации и др.
Идентификация служит для того, чтобы реальный процесс и
модель были близки.Получив модель мы имеем возможность,
используя эту модель, получить близкую к реальной карти-
не ситуацию движения системы и создать управление ситуа-
цией по нашей модели.
Вывод: Модель нужна, чтобы на ЭВМ научиться проектировать
управляемые динамические системы для любых такти-
ческих ситуаций, известных из практики.
Правильно созданная модель - это максимум успеха в проек-
тировании эффективной систе-
мы. После создания и отработки модели стохастической ди-
намической системы создается аппаратура по этой модели,
которая проверяется на динамическом стенде.
Динамический стенд - 2й этап моделирования реальной ситу-
ации уже с аппаратурой.
3й этап состоит в проверке аппаратуры на полигоне.(На
борту транспортного или военного средства).
Моделирование случайных процессов с дискретным временем
(1)  - выборка случайного процесса с дискретным
- выборка случайного процесса с дискретным
временем.
X(t) Процесс (1) в общем виде очень
трудно анализировать, этот про-
цесс, как правило, получен из
эксперимента. Этот реальный
процесс обычно аппроксимируется
другим процессом, который поз-
 волит нам математически созда-
волит нам математически созда-
t вать модели, близкие к реально-
му процессу.
Такое создание моделей называется - аппроксимацией.
Сам аппроксимирующий процесс называется агрегат.
Марковская аппроксимация случайных процессов
Марковским процессом называется такой процесс, у которого
многомерная плотность вероятности
факторизуется в следующем виде:  . Некоторые
. Некоторые
значения фазовых переменных в n-мерном пространстве - это
многомерная плотность вероятности
Двумерная плотность Многомерная ФПВ несет всю ин-
вероятности формацию о случчайном процес-
W(x,y)се. Больше информации не су-
ществует.
Однако использовать эту мно-
гомерную ФПВ чрезвычайно сло-
жно на практике, поэтому час-
то прибегают к некоторым ап-
проксимациям процесса:
Y
X
Аппроксимировать - выбрать такие отсчеты
процесса в моменты времени  , чтобы все
, чтобы все 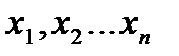 были
были
независимы, тогда многомерная ФПВ факторизуется следую-
щим образом:  - факторизация.
- факторизация.
Однако при такой факторизации может потеряться информа-
ция о случайном процессе. Есть потеря информации для
произвольных отсчетов (кореллированность процесса).
Существует 2й способ аппроксимации - марковский способ
аппроксимации. Для марковских процессов многомерная ФПВ
факторизуется так:
(2)  , где
, где  - ус-
- ус-
ловная плотность вероятности.
Факторизация (2) позволяет сильно упростить математичес-
кие выкладки в задачах фильтрации и управления.
Определение: Процесс называется марковским, если выпол-
няется условие (2)
Оказывается, существует очень много генераторов марковс-
ких процессов. Мы переходим к их рассмотрению.
Процессы авторегрессии
Процесс авторегрессии - простой генератор марковского
процесса.
1. Односвязная регрессия
(3) 
 - задано.
- задано. 
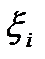 - от генератора белого шума
- от генератора белого шума
 - корреляция.
- корреляция.
 Если а<1, то
Если а<1, то  ®0 имеем
®0 имеем

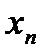 устойчивый процесс.
устойчивый процесс.

 a<1
a<1
Если а>1 - неустой- 
чивый процесс 1 2 3 4 n
 ®¥ (P=1)
®¥ (P=1)
x(t) a=0.9
a³1
a=0.3






1 2 3 4 5 n t
а=1 - модель взрыва. Если 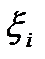 - гауссовский случайный про-
- гауссовский случайный про-
цесс, то легко доказать, что многомерная ФПВ факторизует-
ся.
а - коэффициент регрессии.
Если 0<a<1, то можно доказать, что а - это коэффициент
корреляций между  и
и  .
.
Если процесс изменяется очень медленно, то он сильно кор-
релирован. Коррелированными процессами очень легко управ-
лять и они очень легко анализируются и прогнозируются.
Генератор марковского процесса, реализующий авторегрессию
1-го порядка
(1) 
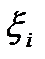 Генератор
Генератор 
 - марковский случайный процесс
- марковский случайный процесс 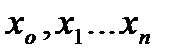
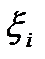 - генератор случайных чисел (в ЭВМ)
- генератор случайных чисел (в ЭВМ)
i = 0,1,2...n
Утверждение (1): процесс (1) является марковским.
Доказательство: Пусть  заданная величина. Процедура (1) называется реккурсивной или иттеративной, рекурент-
заданная величина. Процедура (1) называется реккурсивной или иттеративной, рекурент-
ной.
(2) 
Пусть 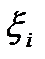 ~
~  , где 0-среднее,
, где 0-среднее,  - дисперсия.
- дисперсия.
В формуле (2) разность имеет гауссовкий процесс распре-
деления  или:
или:
(3) 
(4) 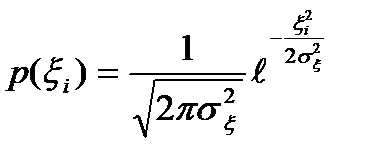
(3) получено из (4) и (2) заменив 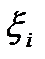 на
на  . Поскольку
. Поскольку
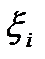 - независимые по условию, то имеем:
- независимые по условию, то имеем:

Утверждение доказано. Процесс (1) является марковским.
Структурная схема генератора марковского процесса
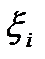

реализация рекурсии

a |¾¾|  рис. 1
рис. 1
T
|¾¾| - линия задержки.
Это структурная схема 4х полюсника, которая реализует
генерацию марковского случайного процесса  . Это генера-
. Это генера-
тор с внешним возбуждением, который возбуждается с по-
мощью независимого гауссовского процесса 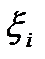 .
.
Сетка дискретного времени:
|¾¾|¾¾|¾¾|¾¾® t
T
Утверждение (2)
На выходе 4х полюсника процесс  ,i=1,2...n - коррелиро-
,i=1,2...n - коррелиро-
ван, с коэффициентом корреляции ‘a’.
Доказательство: Из (1) имеем 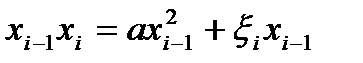 , берем мат-
, берем мат-
ожидание,  ,
,
 ,
,  - коэффициент корреляции.
- коэффициент корреляции.
Утверждение доказано.
Вывод: На вход схемы рис.1 идет некоррелированный слу-
чайный процесс 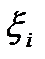 , а следовательно независимый.
, а следовательно независимый.
(если процесс гауссовский и некоррелированный, то
он независимый, для других процессов это неверно)
В природе наиболее часто встречается гауссовский
случайный процесс. На выходе схемы - зависимый
коррелированный марковский процесс, у которого
плотность факторизуется по условным плотностям.
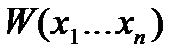 - не факторизуется
- не факторизуется
 - факторизуется
- факторизуется
Процесс (1) называется односвязный марковский
процесс.
Замечание: Процесс (1) получен при дискретизации непре-
рывного линейного диф. уравнения 1-го порядка.
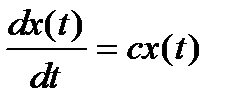 без учета стохастической правой час-
без учета стохастической правой час-
ти 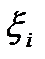
На сетке дискретного времени имеем:
 ;
;  - получаем обычную (не
- получаем обычную (не
стохастическую) авторегрессию.
Tc+1=a
Авторегрессия 2-го порядка - двухсвязный процесс
(1) 
Коэффициенты 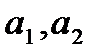 называются коэффициентами регрес-
называются коэффициентами регрес-
сии. Уравнение (1) без стохастической правой части легко
получается из диф. уравнения 2-го порядка. Уравнение (1)
реализует генератор марковского процесса, который называ-
ется двухсвязным в зависимости от входного процесса 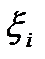 .
.
генератор
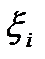 марковского
марковского  рис.2
рис.2
двухсвязного
процесса
На вход генератора действует белый шум. На выходе - двух
связный марковский процесс.
g(f)
белый шум
0 f f
В зависимости от коэффициентов 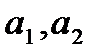 ны выходе будут раз-
ны выходе будут раз-
личные процессы. Процесс (1) получается из линейного диф.
уравнения 2-го порядка, если это диф. уравнение рассмат-
ривать на временной сетке (дискретна во времени).
Известно, что диф. уравнение 2-го порядка имеет реше-
ние в виде комплексной экспоненты, если корни характерис-
тического уравнения комплексные, аналогично для некоторых
значений коэффициентов 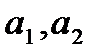 , процесс авторегрессии будет
, процесс авторегрессии будет
иметь вид стохастической синусоиды.
Генератор двухсвязного марковского процесса
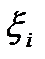

|¾¾| |¾¾|


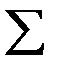 T - период дискретизации
T - период дискретизации
Изменение по синусоиде называется синусоидальный тренд.
Марковский процесс 2-го порядка более богатый, чем 1-го,
с помощью него можно моделировать более сложные процессы.
Авторегрессия m-го порядка
(2) 
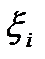 - возбуждающий белый шум.
- возбуждающий белый шум.
Процесс (2) получен из диф. уравнения m-го порядка путем
дискретизации. Это марковский процесс с дискретным време-
нем.
Этот процесс значительно более информативен, чем ра-
нее рассмотренные, ибо он может моделировать сложномоду-
лированные случайные процессы. Он может модулировать АМ,
ЧМ, ФМ путем подбора  , а также подбором
, а также подбором  мож-
мож-
но идентифицировать очень многие случайные процессы ре-
ально существующие на практике, например: хорошо моду-
лируется движение летательнвх аппаратов при маневре (рег-
рессия m=6¸16), речь, полет космического корабля, посадка
на планету.Стохастическая модель удобна потому, что она адекватна реальным ситуациям.
Генератор m-связного марковского процесса
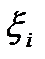

|¾¾|...... |¾¾| |¾¾|



Разностные модели на примере модели 2-го порядка
(3)  - разностная модель 2-го порядка
- разностная модель 2-го порядка
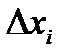 - приращение, характеризует скорость изменения
- приращение, характеризует скорость изменения
процесса
 Модель с приращением удобна в том
Модель с приращением удобна в том
 плане, что не требуется заранее
плане, что не требуется заранее
 знать коэффициенты регрессии.
знать коэффициенты регрессии.


Разностные модели 3-го порядка
(4) 
 - 1-я разность
- 1-я разность
 - 2-я разность
- 2-я разность
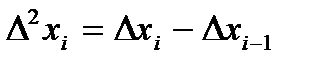
1-я разность характеризует скорость изменения случайного
процесса.
2-я разность характеризует ускорение.
Модель (3) и (4) очень широко иcпользуется на практи-
ке, т.к. здесь почти нет коэффициентов, которые нужно
идентифицировать (а и  ), они легко подбираются на ЭВМ
), они легко подбираются на ЭВМ
по методу наименьших квадратов. Для этого надо иметь ре-
альный процесс отсчетов, модель (4) и нужно воспользо-
ваться следующей формулой МНК/метод наименьших квадратов/
min  где,
где,  - модель,
- модель,

 - реальный процесс
- реальный процесс
Суть МНК состоит в следующем:
Есть m-отсчетов реального процесса, есть m-отсчетов 
модели, составляется сумма квадратов и подбираются пара-
метры (а,  ) так, чтобы минимизировать эту сумму (делает-
) так, чтобы минимизировать эту сумму (делает-
ся это на ЭВМ)(метод перебора) но в авторегрессии m-го
порядка. Сделать это очень сложно.
Модели скользящего среднего
Пусть  - независимая случайная величина, с произвольным распределением (очень часто гауссовское распределение)
- независимая случайная величина, с произвольным распределением (очень часто гауссовское распределение)
М  =0; М
=0; М  =
=  ;
; 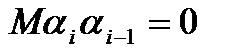 (процесс не коррелирован)
(процесс не коррелирован)
Тогда процесс
(1) 
называется процессом скользящего среднего. Этот
процесс сформирован полностью из шума  (из белого шума)
(из белого шума)
путем сдвига и весового суммирования.
( - весовые коэффициенты). Сумма (1) генерирует
- весовые коэффициенты). Сумма (1) генерирует
процесс  . Процесс
. Процесс 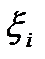 - коррелированный марковский
- коррелированный марковский
процесс. 
Генератор скользящего среднего для формулы (1)


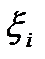
a

i
x

: 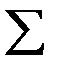 i
i
:

Модель авторегрессии и скользящего среднего

авторегрессия скользящее среднее
 генератор генератор
генератор генератор 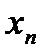
случайного сигнала авторегресии
Здесь  - белый шум;
- белый шум;
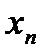 - марковский(модельный)процесс, n=1,2....
- марковский(модельный)процесс, n=1,2....
Между генераторами процесс коррелирован.

Многомерная марковская модель
(1)  , где
, где 
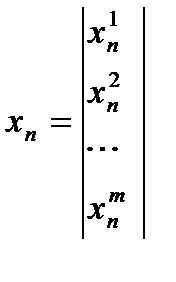 ;
; 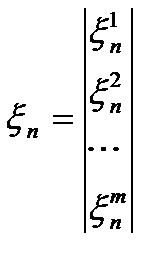 ;
; 
Это самая распространенная модель
(2) 
В модели (1) шумы характеризуются матрицей ковариации в
отличие от авторегрессии, под которой понимается следую-
щее:
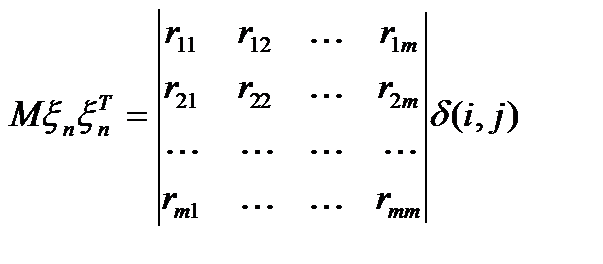 ;
;  ;
; 
 - столбец
- столбец
 - строка
- строка
Элементы матрицы  состоят из корреляции внутри столбика
состоят из корреляции внутри столбика
шума. Столбики между собой коррелированы.
Модель нелинейной регрессии
(3) 
(4) 
В формулах (3)(матричная форма записи),и (4)(скалярная
форма записи) индексы при ‘Х’ это не степени, а номера в
формуле столбика.
(3) и (4) - самая информативная модель, все предыдущие
модели получаются как частный случай из этой модели. Нап-
ример модель речи линейная и нелинейная, но нелинейная
более точная.
Глава 4
Динамические системы наблюдаемые на фоне
шумов
Одномерные динамические системы и фильтр Калмана
(1)  ;
; 
Шумы 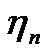 - называются шумами наблюдения (для активных по-
- называются шумами наблюдения (для активных по-
мех). Задачу фильтрации будем решать методом наименьших
квадратов. Задача фильрации требует уменьшить 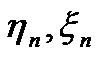 .
.
Вводим эмпирический риск:
(2) 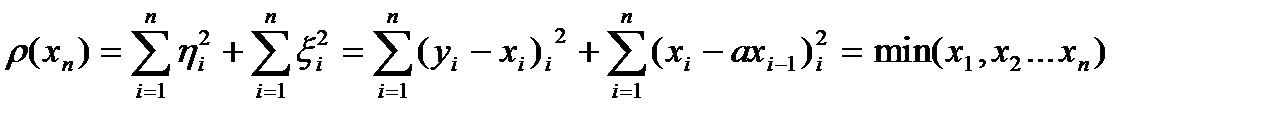
- Это есть классическая запись метода наименьших квадра-
|
|
|
|
|
Дата добавления: 2014-12-16; Просмотров: 910; Нарушение авторских прав?; Мы поможем в написании вашей работы!