Использование преобразования Лапласа 5 страница

f

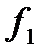
Ф-2 Df

f

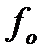
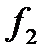
Дискриминационная характеристика - это разность фильтров

Ф-1 и Ф-2. Она формирует невязку .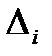

(1)

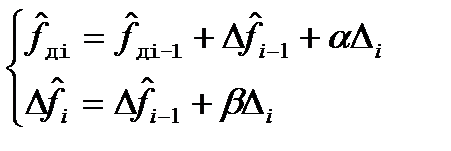
Эта система используется для оценки доплеровской частоты,

меняющейся во времени. Это следует из уравнения (1), где

нижнее уравнение дает поправку доплеровской частоты за

один шаг.Невязка формируется также как в a,b,g - фильтрах.

Глава 7

Устойчивость стохастических систем

В радиоавтоматике все без исключения системы являются

стохастическими, т.е. сама динамическая система описыва-

ется стохастическими разностными уравнениями. Наблюдения

тоже записываются с учетом шумов.

1) Линейные стохастические системы

(1) ;

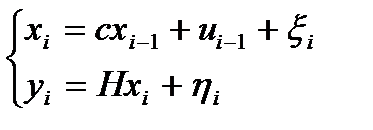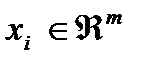
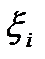- шум динамической системы

- шум наблюдений

- m-мерный вектор

с - матрица перехода

Устойчивость определяется нормой матрицы ‘c’.

Достаточным условием устойчивости (1) является:

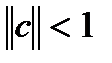, где

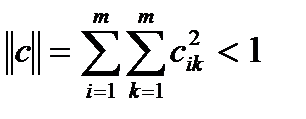(2) , где 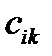- элементы матрицы ‘c’

с =| 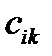|, i=1,...,m; k=1,...,m

Если условие (2) выполняется, то система всегда бу-

дет устойчива.

Замечание: В некоторых случаях система может быть устой-

чивой, если 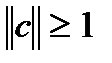, потому что условие (2) яв-

ляется достаточным, но не необходимым.

Пример стохастической системы 1-го порядка:

(1)’

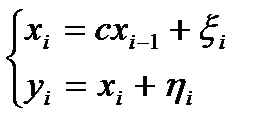
Оценка 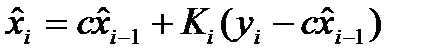- система будет устой-

чива при 0<c<1.

, 0<c<1 - является необходи-

c>1 мым и достаточным условием

устойчивости системы.

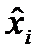
Устойчивость нелинейных систем

Нелинейная стохастическая система:

(3)

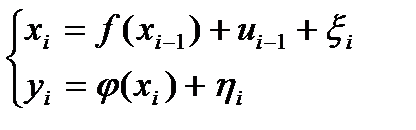
Устойчивость нелинейных динамических систем опре-

деляется функцией Ляпунова.

Определение устойчивости по Ляпунову для детерминирован-

ной системы.

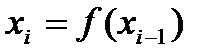
Вводится специальная функция, называемая функцией Ляпуно-

ва. Обозначается: 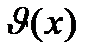. Функция удовлетворяет следующим

условиям:

1. Если x=0, то 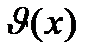=0

2. Приращение функции Ляпунова во времени D 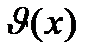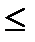0,

т.е. функция должна быть убывающей: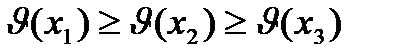

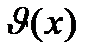Для стохастической системы (3)

обычно функцию Ляпунова выби-

рают так: 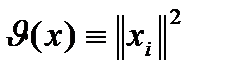. А условие

устойчивости для системы (3)

будет следующим:

1) ,

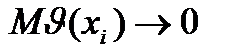i®¥ (ассимптотически)

2)

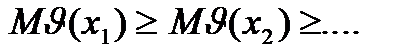
Анализ качества работы стохастических систем радиоавтома-

тики

Качество линейных и нелинейных стохастических систем оп-

ределяется реальным качеством фильтра. (см. выше)

Синтез предполагает, что модель соответствует реальному случайному процессу, который мы фильтруем. В этом случае

качество определяется следующим образом:

Пример: Одномерный фильтр Калмана.

Фильтр: ;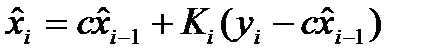

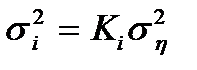
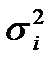
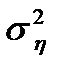- шум наблюдений

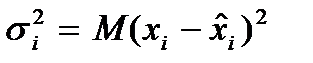
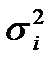- апостариорная дисперсия

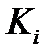- коэффициент усиления

фильтра Калмана

i - дискретное время

Модель:

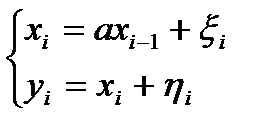
Качество фильтрации определяется адекватностью модели и реального процесса. Как проверить адекватность модели

реальному процессу? Сделать это

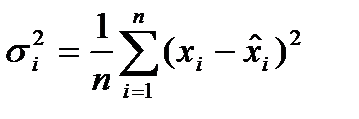можно только по невязке: ,

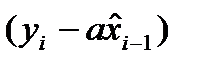где .

i

Теорема: Процесс тогда и только тогда адекватен модели,

когда невязка является белым шумом.

Замечание: Это может случиться только тогда, когда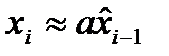

Проблема качества определяется проблемой экстраполяции.

Дата добавления: 2014-12-16