Использование преобразования Лапласа 4 страница

Уравнение (6) позволяет в реккурентной форме вы-

вычислить управление, шаг за шагом, от точки N

до 1 (из будущего в прошлое) получить минимиза-

цию (6) на каждом шаге. Получить 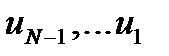. Значе-

ния управления фактически получаются методом пе-

ребора. Оптимальная траектория 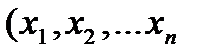) неиз-

вестна до самого последнего шага.

Если задача имеет большую размерность, то

сложность при вычислении очень большая. Если

вводить динамические системы (т.е. модели), то

можно значительно упростить метод нахождения оп-

тимального управления. Т.е. получить управление

в замкнутом виде (в виде некоторой формулы).

Синтез оптимального управления для марковских динамичес-

ких систем.

(1) 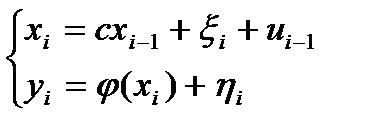; ; 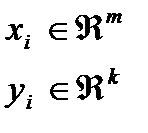; где -

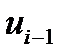- управление; - шум динамической системы.

Управление должно менять - траекторию, и изменять ее так, чтобы минимизировать средний критерий качества,

причем управляется динамическая система не по всем коор-

динатам.

- управляемый случайный процесс.

Динамическая система, сама как таковая, не наблюдается, а

наблюдается j()(нелинейно преобразованная фазовая пере-

менная) с шумом. В этом случае говорят, что динамическая система ненаблюдаема напрямую. Для того, чтобы сделать ее

наблюдаемой необходимо использовать теорию нелинейной

фильтрации (см. предыдущие лекции).

В этом случае получаем оценку нелинейной динамической

системы в условиях линеаризации по Тейлору:

(2)

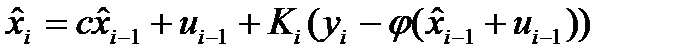
Синтез оптимального управления используя (2) проведем применив квадратичный критерий качества, причем управле-

ние динамической системой будем вести к некоторому этало-

ну, т.е. задано: 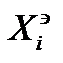, i=1,2...n

Критерий оптимизации

(3) ;

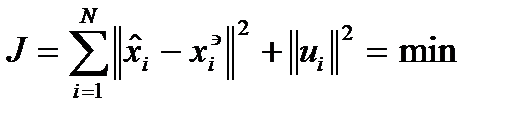где || - норма, .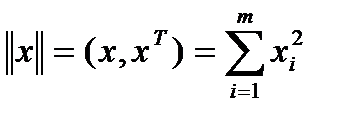

Риск складывается из двух слагаемых:

1-е слагаемое: Это есть квадрат отклонения траектории от

эталона. Оно должно быть минимизировано с

учетом формулы (2).

2-е слагаемое: Это есть сумма с квадратом самого управ-

ления (некоторая сила) должны быть мини-

мизированны (так должно быть всегда)

Минимизация (3) - это достаточно сложная задача вариаци-

онного исчисления (просто взять здесь производную по ‘u’

не удается).

Для минимизации (3) используем уравнение Бэлмана:

(4)

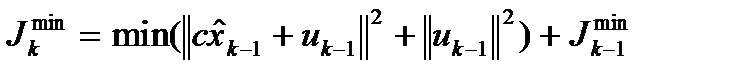
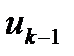
В формуле (4) минимизируя шаг за шагом получим:

(5) 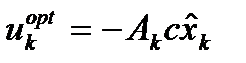; где 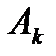- матрица

Выводы: (к формуле (5))

Оптимальное управление (5) реализуется с ис-

пользованием линейной оценки динамической сис-

темы, и это управление вставляется в формулу:

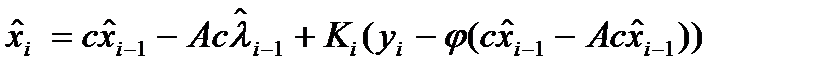
Если упростить критерий и привести его к виду (3’):

(3’)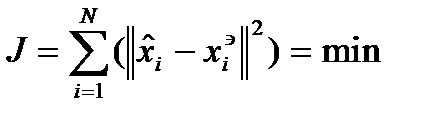

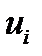
то минимизация дает оптимальное управление эталона:

(6)

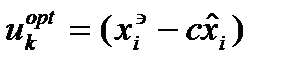
Оптимальное управление пропорционально разности меж-

ду экстраполированной оценкой и эталоном, т.о. полу-

чим:

(7)

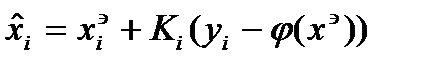
Оценка (7) подставляется в (6). Со временем, при ми-

нимизации в этом случае сама оценка устремляется к

эталону.

Пример синтеза динамической системы управления частотой

генератора

Общая постановка:

Пусть имеется некоторая эталонная траектория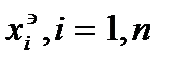

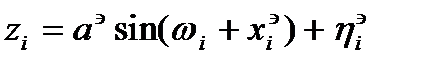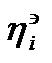(1) , где - шум

Если эталон защищен, то его фильтруют.

Имеется управляемая динамическая система:

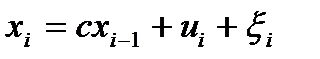
Управляемая динамическая система - фаза генератора или

траектория, которая должна подстроиться под эталон.

(2) 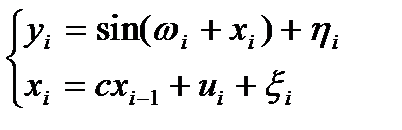; шума часто нет, поэтому

им пренебрегают. Пусть

(3)

Рассмотрим более сложную модель фазы рассматриваемого ге-

нератора.

(4)

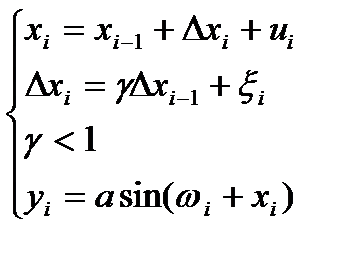
Считаем, что в (1),(3) уход фазы очень медленный,т.е.

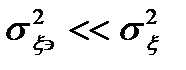. Используя нелинейную функцию оценка эталона:

(4’)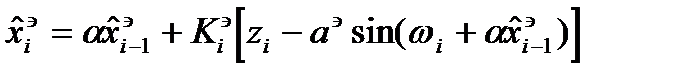

В (4) решение уравнения относительно имеет вид:

(5) 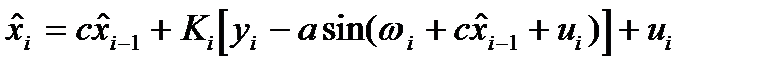; с<1.

Выше было доказано, используя уравнение Бэлмана,

что:

(6)

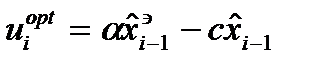
Структурная схема реализации оптимального управления под-

стройки частоты к эталону

(4’) (5’)

шум

эталонный нелиненый Решающее Подстраи-

генератор фильтр 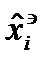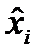устройство ваемый ге- вых

Т Т нератор

a c

устройство

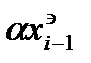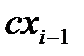+ - управления

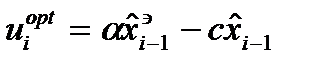
На выходе - частота подстраиваемого генератора.

Подстраиваемый генератор имеет следующий вид:

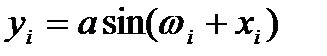
- изменяется по закону (4), управляющая функция воз-

действует /вырабатывающаяся на прошлом шаге (i-1)/ она

должна подстраивать генератор так, чтобы она стремилась

к эталону.

Для этого: имеется устройство управления, которое воз-

действует на контур подстраиваемого генератора так, чтобы

(путем воздействия на варикап) 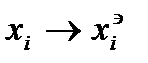; a = с, тогда .

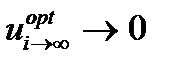Управляемая система с обратной связью: если есть откло-

нение фазы на 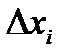, (т.е. отклонение частоты) (),

тогда решающее усторойство дает оценку . Это приведет к

тому, что отклонится, напряжение подается на устрой-

ство управления, которое ликвидирует приращение. (правое

кольцо называется - кольцо ФАПЧ).

Глава 6

Управление нелинейными динамическими систе-

мами с помощью отрицательной обратной связи

Постановка задачи

Определение: Следящим измерителем называется система,

осуществляющая оценку некоторого параметра

(который является случайным процессом) в

следящем режиме.

Параметр может иметь следующий физический смысл:

а) Угловые координаты некоторого летательного аппарата,

которые изменяются во времени.

б) Изменение во времени доплеровской частоты.

в) Дальность до объекта.

Пример: летательный аппарат

D(t) - дальность

z 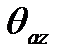(t) - угол азимута

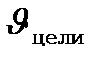
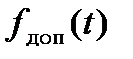- доплеровская частота

D

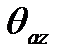X Все эти 3 параметра входят в

y некоторый сигнал.

Y y - угол места

;

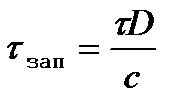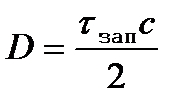
Доплеровская частота: Любая движущаяся система, облучае-

мая электромагнитной энергией, из-

лучает эту энергию.

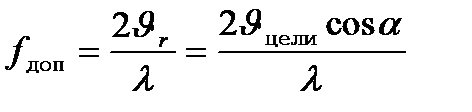; где 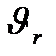- радиальная скорость.

Структурная схема следящего измерителя

y(t)=S(t,q(t))+h(t))

+ D(t) Фильтр

Дискриминатор экстраполя-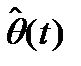

тор

-

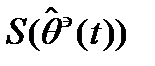
рис.1

Синтезатор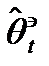

опоры (блок 3)

D(t) - невязка.

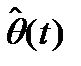- оценка.

Эта схема была построена в 30х годах инженерами-учеными.

Однако сначала 60х годов оказалось, что ее можно синтези-

ровать, используя теорию нелинейной фильтрации.

На рис.1 представлена схема следящего измерителя, где

управление осуществляется с использованием ООС. Эта

структура состоит из 3х блоков.

1й блок: - дискриминатор. На вход его подается смесь сиг-

нала S(t,q(t))+h(t) (аддитивная смесь), где

q(t) - меняющийся парметр. Нужно получить его оценку .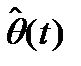

На другой вход дискриминатора подается копия сигнала S(t,q(t)), которая должна повторять сигнал, спрятанный в

шумах. Это достигается путем экстраполяции (предсказание) случайного процесса. На входе дискриминатора образуется

невязка: 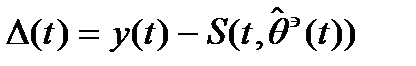- это есть невязка нелинейной

фильтрации.

2й блок: - фильтр экстраполятор (блок фильтрации). На его

вход поступает невязка. 2й блок формирует те-

кущую оценку случайного процесса q(t). Это окончательный

нелинейный фильтр - расширенный фильтр Калмана. В этом же

блоке формируется оценка экстраполяции (см. далее) и эта

оценка подается на синтезатор опоры.

3й блок: - формирует копию сигнала. Оценка q(t) формиру-

ется по следующему критерию: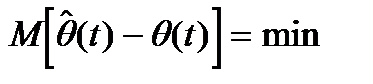

- критерий среднеквадратической ошибки.

Оптимальная оценка по критерию минимума среднеквадрати-

ческой ошибки получается с помощью только лишь нелиней-

ной фильтрации.

Замечание: Фильтрация нелинейна потому, что невязка фор-

мируется нелинейно (оцениваемый параметр

q(t) входит в сигнал нелинейно), S(t,q(t)) -

нелинейно.

Принцип экстраполяции для задач синтеза следящих измери-

телей управляемых с помощью ООС

Следящий измеритель отслеживает некоторый (многомерный)

параметр 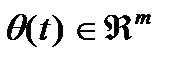, причем имеются наблюдения:

(1) 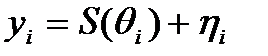, где 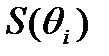- некоторая нелинейная

функция

В радиоавтоматике,в непрерывном времени это выглядит так:

, где 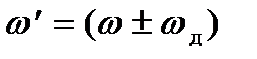; 0<t<T.

А -амплитуда гармонического колебания, которая, например,

несет информацию об угловом положении цели.

Т - время наблюдения

t - время запаздывания, несет информацию о временном по-

ложении сигнала

t Т

t

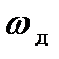- доплеровская частота.

y(t)- модуляция сигнала (известна заранее)

j(t)- некоторая начальная фаза сигнала, которая несет ин-

формацию об угловом положении цели. Либо j(t)- ме-

шающий параметр.

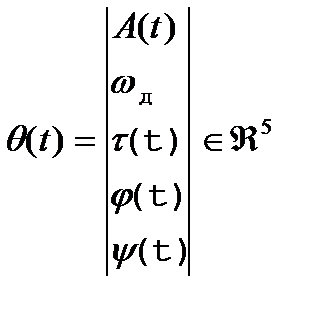
Система слежения за q(t) - следящий измеритель. Общий

вид записи см. (1).

Решение проблемы синтеза следящего измерителя:

Пусть q(t) 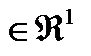.Рассмотрим q(t) на дискретной сетке ® ,

где 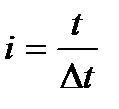, Dt - интервал дискретизации.

(2) 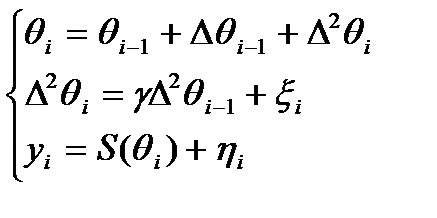; g<1

(3) 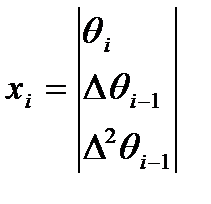- 3х мерный вектор,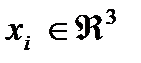

- фазовая координата

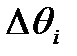- приращение скорости

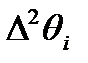- ускорение (второе приращение)

Используя (3) модель (2) преобразуется:

(4)

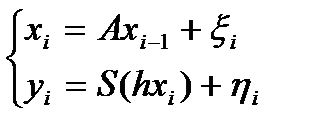
h=|1 0 0| - вектор 3´3,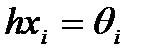

А - матрица 3´3, такая, что получается модель (2).

Используя модель (4) видим, что верхнее уравнение линей-

ное, а нижнее уравнение нелинейное. Используя теорию не-

линеной фильтрации получим оценку:

(5)

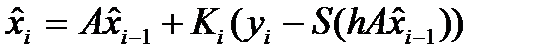
(5) - уравнение нелинейной фильтрации.

Структурная схема, которая реализует алгоритм следящего

измерителя (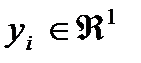) выглядит так:

дискриминатор фильтр экстраполятор

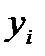+ S

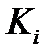
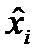
А

Dt

синтезатор

опоры

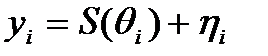
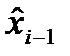
Экстраполяция.a,b,g - фильтры

Реализация нелинейного фильтра по формуле (5) несмотря на ее реккурентный характер достаточно сложна для реализации

на сигнальных процессорах, поэтому часто используют еще

одно упрощение - переходят от векторно-матричной записи

нелинейной фильтрации по формуле (5) к скалярной записи.

(заметим, что формула (5) реализует следящий измеритель

некоторого параметра)

a,b,g - фильтры значительно упрощают синтез следящих

измерителей. Идея состоит в том, что вместо матричного

коэффициента 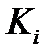в формуле (5) подставляются скалярные ве-

личины.

Проектирование a,b,g - фильтра

Модель:

; а<1

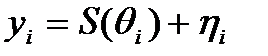- скалярное наблюдение

Был введен параметр:

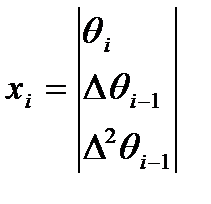
Поскольку мы ввели этот параметр, фильтр получился 3х

мерный. Далее вместо фильтра (5) запишем эвристический

фильтр: (Эвристика - полуинтуитивное мышление)

(6)

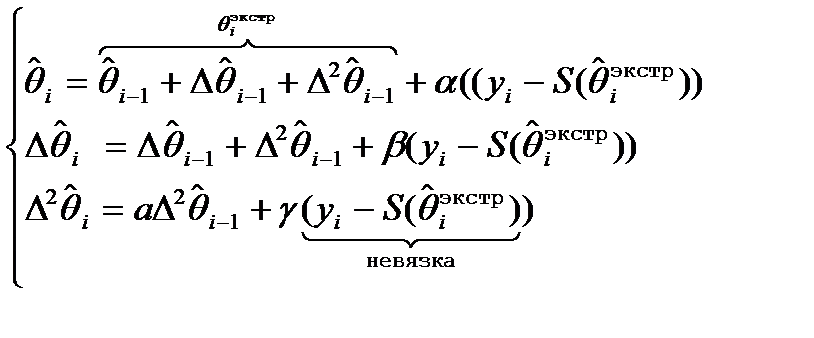
a<1, b<1, g<1

(7)

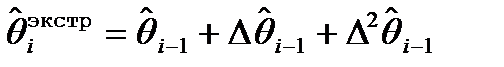
Комментарии к (6) и (7): Справа - невязки, взяты из тео-

рии нелинейной фильтрации. Од-

нако в (6) экстраполированное значение получается из фор-

мулы (7). (7) - это кусок ряда Тейлора.

В нелинейной фильтрации экстраполяция получается ав-

томатически. А здесь мы ее искусственно создали в формуле

(7), но она очень сильно близка к формуле (5).

|

Фильтрация | Первое слагаемое в (6) (верхняя строка) есть

координаты | 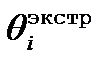, плюс взвешенный, с весом a корректи-

| рующий член, который есть невязка. Эта невя-

| зка корректирует экстраполяцию за счет ново-

| го наблюдения.

|

Фильтрация | Первое слагаемое во второй строке (6) - есть

приращения | экстраполяция полного приращения()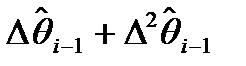

|

| 3-я формула в (6) - фильтрация второго при-

| ращения координаты.

|

Коэффициенты a,b,g получаются экспериментально.

(8) 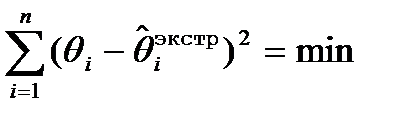} -подбор a,b,g

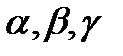
(8) - метод наименьших квадратов, подбор a,b,g на ЭВМ.

Структурная схема следящего измерителя за параметром

по формулам (6), (7).

формирователь невязки

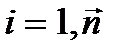
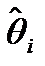
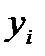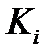+ S S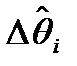

-

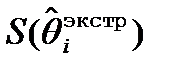
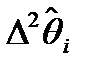
Синтезатор 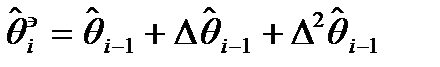A

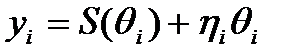опоры S(×)

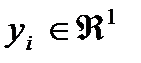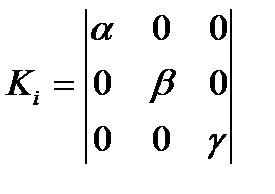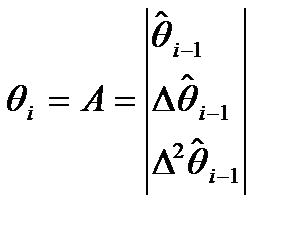; ; Þ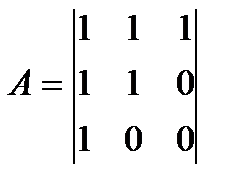

Синтез следящего измерителя доплеровской частоты

Постановка задачи 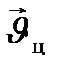- вектор скорости

цели

Имеется РАС.

Посылается сигнал от РАС

с частотой 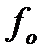. l=1¸3см. Обратный сигнал будет на частоте

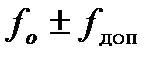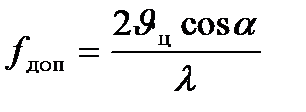; . Доплеровская частота используется

для повышения помехоустойчивости РАС и для наведения ра-

кет. Поскольку цель движется, то меняется a и следова-

тельно и 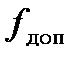. Отсюда вывод: за доплеровской частотой нуж-

но следить.

Проблема: синтезировать следящий измеритель доплеровской

частоты.

Приходящий сигнал:

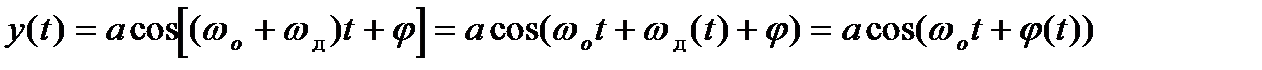
j(t) будем записывать в дискретные моменты времени.

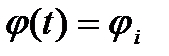, i=1,2,...n;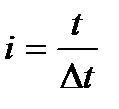

Дискретная модель фаз:

(1) ;

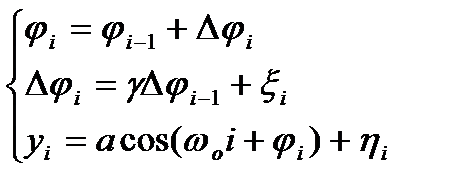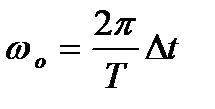; ; T - период колебания.

g<1, такой, чтобы система была устойчива. Предполагаем,

что за Dt не меняется .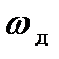

Синтез цифрового оптимального следящего измерителя доп-

леровской частоты.

y(t)=Acos(wt+j(t))+h(t)

j(t) - фаза, которая содержит доплеровскую частоту

j(t)=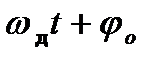

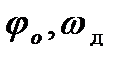- неизвестны, но постоянны.

Обычно для реализации цифрового измерителя используется

квадратичный канал:

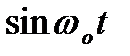
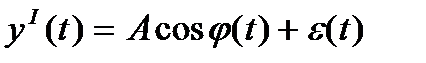
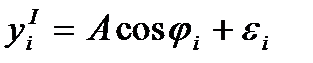
´ RC-фильтр АЦП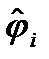

Оптималный

рис. 1 нелинейный

y(t) тактовая ¾® фильтр (3)

синхронизация

´ RC-фильтр АЦП

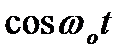
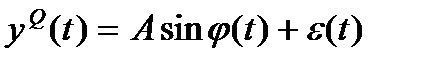
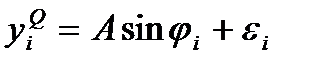
После такого преобразования снимается несущая, остается

только доплеровская частота.

e(t) - низкочастотный шум.

Acosj(t),Asinj(t) - НЧ компоненты.

На большей 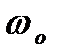требуются очень сложные и дорогие АЦП.

После цифровой обработки (АЦП) модель записывается:

(2) 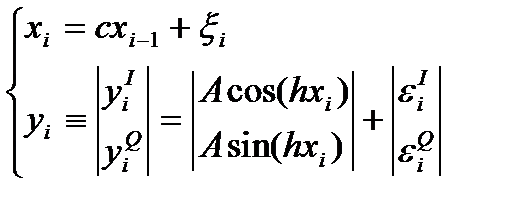, где ;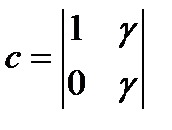

h = |1 0|; ;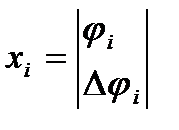

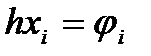
Вектор динамической системы двумерный и динамическая сис-

темы тоже двумерная.

(3)

Фильтр (3) дает оцнеку . Реализация невязки ана-

логично как в a,b,g - фильтрах.

Синтез аналого-цифрового следящего измерителя.

Рис. 2 Ф-1 Д АЦП Фильтр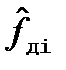

Калмана

экстра-

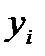УПЧ ´ Ф-3 полятор

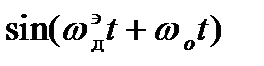Ф-2 Д АЦП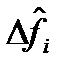

Синтезатор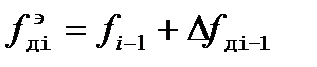

опоры

Ф-3 - узкополосный фильтр

Ф-1,Ф-2 - расстроенная пара фильтров

Ф-1 Дискриминационная

характеристика:

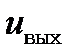вычитателя

Дата добавления: 2014-12-16