Свойства математического ожидания дискретной случайной величины

1. Математическое ожидание постоянной величины С равно этой величине.

Постоянную С можно рассматривать как дискретную случайную величину, принимающую лишь одно значение С с вероятностью р = 1. Поэтому M(С) = С 1 =

= С.

2. Постоянный множитель можно выносить за знак математического ожидания, т. е. М(СХ) = С М(Х).

Используя соотношение (9.1), имеем

М(СХ) =C х ₁ р ₁ +Cх₂р₂ +... +Cх_n р _n.= = С(х ₁ р ₁ +х₂р₂ +... +х_n р _n.) = =СМ(Х).

Следующие два (3 и 4) свойства примем без доказательства.

3. Математическое ожидание суммы двух случайных величин X и Y равно сумме их математических ожиданий:

М(Х +Y) = М(Х) + М(Y).

Определение. Случайные величины X и Y называют независимыми, если закон распределения каждой из них не зависит от того, какое возможное значение приняла другая величина.

Примером двух независимых случайных величин могут служить суммы выигрышей по каждому из двух билетов по двум различным денежно-вещевым лотереям. Здесь ставший известным размер выигрыша по билету одной лотереи не влияет на ожидаемый размер выигрыша и соответствующую ему вероятность по билету другой лотереи.

Несколько случайных величин называют независимыми, если закон распределения любой из них не зависит от того, какие возможные значения приняли остальные случайные величины.

4. Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий:

М(Х Y) = М(Х)×М(Y).

Следствием свойств 2 и 3 является свойство 5. 5. Математическое ожидание разности двух случайных величин X и Y равно разности их математических ожиданий:

М(Х -Y) = М(Х) - М(Y).

Примечания. 1. Свойства 3 и 4 имеют место и для любого конечного числа случайных величин.

2. Если множество возможных значений дискретной случайной величины X бесконечно, то математическое ожидание М(Х) определяется суммой числового ряда М(Х) = 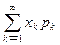при условии, что этот ряд абсолютно сходится (в противном случае говорят, что математическое ожидание М(Х) не существует). Перечисленные свойства математического ожидания остаются в силе [4] и для таких случайных величин.

Пример 9.4. Найдем математическое ожидание случайной величины

Z = X + 2 Y, если известны математические ожидания случайных величин Х и Y: М(Х) = 5,М(Y) = 3.

Решение. Используя свойства 3 и 2 математического ожидания, по­лучаем

М(Z) = М(Х + 2Y) = М(Х) + М(2Y) = М(Х) + 2М(Y) =5 + 2×3 = 11.

Пример 9.5. Независимые случайные величины заданы законами распределения

X
р	0,2	0,8

Y	0,5
р	0,3	0,7

Найти математическое ожидание случайной величины ХY

Решение. Найдем математические ожидания каждой из данных величин:

М(Х) = 1×0,2 + 2×0,8 = 1,8,

М(Y) = 0,5×0,3 + 1×0,7 = 0,15 + 0,7 = 0,85.

Случайные величины Х и Y независимы, поэтому искомое математическое ожидание

М(ХY) = М(Х)×М(Y) = 1,8×0,85 = 1,53.

Дата добавления: 2014-11-29