Декартовы прямоугольные координаты

Проекция вектора

Решение.

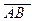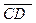+ =3+(-5)=-2.

Рис. 1.3

Имеет место утверждение: при любом расположении трех точек на оси величины векторов 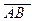, 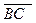и удовлетворяют соотношению 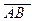+ 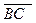= (основное тождество).

Доказательство представлено на рис. 1.4, где показаны всевозможные случаи расположения трех точек A, B, C на оси l.

+ =

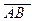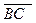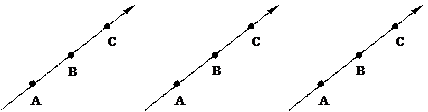
Рис. 1.4

Проекцией вектора на заданную ось l называется величина вектора на оси l (рис. 1.5а). Проекцией вектора 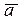на вектор 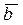называется проекция вектора на ось, проходящую через вектор 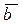и имеющую с ним одинаковое направление (рис. 1.5б).

Рис. 1.5а Рис. 1.5б

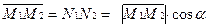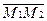Пр , где - угол между вектором и осью l.

Свойство проекций:

1) Проекция суммы векторов на ось равна сумме проекций этих векторов, т.е. Пр_l Пр_l + Пр_l ;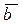

2) проекция произведения вектора 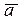на число 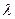равна произведению числа на проекцию вектора 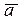, т.е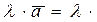. Пр_l Пр_l .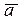

Положение точки в пространстве будем определять относительно пространственной декартовой прямоугольной системы координат, состоящей из трех взаимно перпендикулярных осей координат, пересекающихся в одной и той же точке О, называемой началом координат.

Ось Ox называют осью абсцисс, ось Oy - осью ординат и ось Oz -осью аппликат.

Координатные оси Ox, Oy, Oz, взятые попарно, определяют три взаимно перпендикулярные плоскости xOy, yOz, xOz, называемые координатными плоскостями.

Декартова система координат позволяет связать с каждой точкой P пространства, в котором выбраны три не лежащие в одной плоскости направленные прямые Ox, Oy, Oz (оси координат), пересекающиеся в начале O, три вполне определенных действительных числа (декартовы координаты) x, y, z; при этом пишут P(x, y, z).

Оси Ox, Oy, Oz могут образовывать правую или левую систему. Для правой системы поворот от оси Ox к оси Oy на угол, меньший 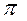, совершается в направлении против часовой стрелки, если смотреть на плоскость xOy из какой-либо точки положительной полуоси Oz (положительная сторона плоскости xOy). Смотрите рис.1.6.

Правая система Левая система

Рис. 1.6

Замечание. Наряду с декартовой системой координат рассматривается полярная система координат на плоскости, которая задается точкой О (полюсом) и полярной осью - лучом, выходящим из полюса. Связь прямоугольных и полярных координат задается формулами:

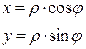, где 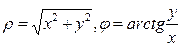(1.3.1)

Дата добавления: 2014-11-29