Вопросы для самопроверки. Двойное векторное произведение трех векторов

Двойное векторное произведение трех векторов

Двойным векторным произведением трех векторов называется произведение вида:

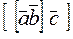(1.9.1)

Так как оно часто используется в приложениях, покажем, что его вычисление можно свести к вычислению более простого выражения, т.е. справедливы следующие равенства:

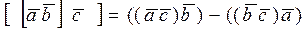(1.9.2)

Прежде всего отметим, что двойное векторное произведение трех векторов

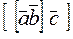есть вектор, компланарный с векторам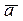и и .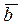

1. Дайте определение понятия вектора.

2. Какие векторы называются коллинеарными, компланарными?

3. Основные операции над векторами.

4. Что называется проекцией вектора на заданную ось? Свойство проекций.

5. Дайте определение декартовой прямоугольной системы координат. Векторы в декартовой системе координат.

6. Какая система координат называется полярной? Связь прямоугольных и полярных координат.

7. Запишите операции сложения и умножения вектора на число в координатной форме.

8. Скалярное произведение двух векторов. Определение.

9. Свойства скалярного произведения.

10. Координатная форма записи скалярного произведения.

11. Условия коллинеарности и перпендикулярности векторов. Определение. Свойства.

12. Векторное произведение двух векторов. Определение. Свойства.

13. Координатная форма записи векторного произведения.

14. Смешанное произведение. Свойства.

15. Понятие двойного векторного произведения трех векторов.

Дата добавления: 2014-11-29