
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Векторное и нормальное уравнение плоскости
|
|
|
|
Уравнение в отрезках
Пусть в уравнении Ax+By+Cz+D = 0, A¹0, B¹0, C¹0, D¹0,
т.е. плоскость пересекает все три оси координат и не проходит через начало.
Преобразуем уравнение следующим образом: Ax + By + Cz = -D
x/(-D/A) + y(-D/B) + z(-D/C) = 1, обозначив a = (-D/A); b = (-D/B); c = (-D/C), будем иметь
x/a+y/b+c/z=1 (6.2.1)
Уравнение (6.2.1) называется уравнением плоскости в отрезках.
Пусть в пространстве заданы система прямоугольных декартовых координат и некоторая плоскость p (рис. 6.2), положение которой определено единичным вектором 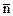 , имеющим направление перпендикуляра OD, опущенного на плоскость из начала координат, и длиной p этого перпендикуляра.
, имеющим направление перпендикуляра OD, опущенного на плоскость из начала координат, и длиной p этого перпендикуляра.
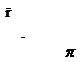
Рис. 6.2
Произвольную точку плоскости М мы будем обозначать двояким образом: либо при помощи её координат в виде M(x,y,z), либо при помощи её радиус-вектора – в виде 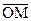 =
= 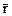 ; оба способа равнозначны, поскольку
; оба способа равнозначны, поскольку 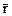 =x
=x 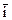 + y
+ y 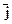 + z
+ z 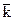 .
.
При любом положении точки М на плоскости p проекция её радиуса вектора 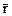 на направление вектора
на направление вектора 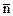 всегда равна p:
всегда равна p: 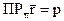 (6.3.1)
(6.3.1)
Но это равенство можно записать используя скалярное произведение.
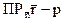 = (r,n) - p = 0 (6.3.2)
= (r,n) - p = 0 (6.3.2)
Это векторное уравнение плоскости p.
От векторного уравнения перейдём к её координатному уравнению.
Обозначим через a, b, g углы образованные единичным вектором 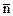 с ортами
с ортами 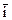 ,
, 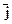 ,
, 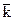 . Тогда cosa, cosb и cosg будут координатами этого вектора:
. Тогда cosa, cosb и cosg будут координатами этого вектора:
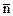 =
= 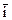 cosa +
cosa + 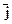 cosb +
cosb + 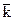 cosg (6.3.3)
cosg (6.3.3)
Кроме того, известно, что 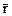 = x
= x 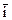 + y
+ y 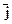 + z
+ z 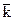 (6.3.4)
(6.3.4)
Используя формулы (6.3.3) и (6.3.4) выразим (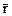 -
- 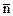 ) - p = 0 в координатной форме:
) - p = 0 в координатной форме:
(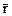 ,
, 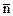 ) - p = x cosa + y cosb + z cosg – p = 0 (6.3.5)
) - p = x cosa + y cosb + z cosg – p = 0 (6.3.5)
Это нормальное уравнение плоскости в координатной форме.
Пусть теперь дано какое-нибудь уравнение плоскости p: Ax + By + Cz + D = 0 (6.1.2)
Как, отправляясь от этого уравнения, получить нормальное уравнение той же плоскости?
Так как уравнения (6.3.5) и (6.1.2) определяют одну и ту же плоскость p, то их соответствующие коэффициенты пропорциональны, т.е.
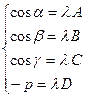 (6.3.7)
(6.3.7)
при некотором l, из равенств (6.3.7) определяем l: ôlô= 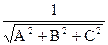 (6.3.8)
(6.3.8)
Знак l определяем для случая D¹0 из четвёртого равенства (6.3.7); так как p>0, то lD<0 и, следовательно, l имеет знак, противоположный знаку D.
Определение: Число l, имеющее модуль 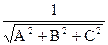 и знак, противоположный знаку коэффициента D, называется нормирующим множителем уравнения (6.1.2). При D=0 можно знак l выбрать произвольно.
и знак, противоположный знаку коэффициента D, называется нормирующим множителем уравнения (6.1.2). При D=0 можно знак l выбрать произвольно.
Мы установили: для того, чтобы из общего уравнения плоскости (6.1.2) получить нормальное уравнение плоскости (6.3.5), надо обе части уравнения (6.1.2) помножить на нормирующий множитель этого уравнения.
|
|
|
|
|
Дата добавления: 2014-11-29; Просмотров: 1123; Нарушение авторских прав?; Мы поможем в написании вашей работы!