
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Минимизация функции алгебры логики
|
|
|
|
Свойства алгебры Жегалкина
1. Коммутативность
x Å y = y Å x
2. Дистрибутивность
x & (y Å z)= x & y Å z & x
3. Идемпотентность
x Å x = 0
x Å 0 = x
Для алгебры Жегалкина характерно
 = x Å 1
= x Å 1
x Ú y = x & y Å x Å y
Определение. Формула, имеющая вид полинома по модулю 2 называется полиномом Жегалкина для функции алгебры логики.
Замечание. От булевой формулы всегда можно перейти к полиному Жегалкина.
Работа автомата может быть полностью описана с помощью следующей системы функций алгебры логики [2]:
y1= f1 (x1... xn)
y2= f2 (x1... xn)
...
ym= fm (x1... xn).
Здесь Pi = (X1, X2,...,Xn); Qj = (y1, y2,...,ym) - соответственно входное и выходное слово. Работа автомата может быть задана либо в виде конечных таблиц, либо в виде аналитической записи функций fi.
Проблема полноты системы функций эквивалентна проблеме выбора стандартного набора элементов, из которого будет строиться автомат (блок вычислительной техники), при этом все функции fi должны быть выражены через базисные функции. Уменьшение числа функций в базисе приводит к уменьшению стандартных элементов, на которых строится схема, однако, при этом увеличивается общее число элементов схемы и возникает задача о “простейшем” представлении логических функций через систему базисных функций. Для этого используют методы минимизации:
n метод вынесения за скобки;
n метод неопределенных коэффициентов;
n метод с использованием карт Карно;
n метод Мак - Класки;
n метод Блэка.
Рассмотрим метод минимизации СДНФ с помощью карт Карно. Карта Карно - это диаграмма, состоящая из 2n квадратов, где n - число переменных. Клетка карты - одна из возможных конъюнкций, входящих в СДНФ. Минимизация на основе карт Карно осуществляется путем локализации на карте прямоугольных областей из числа клеток кратного 2.
Для работы с картой необходимо по таблице истинности составить СДНФ, затем для каждой элементарной конъюнкции проставить 1 в соответствующие клетки карты. Затем единицы объединяются таким образом, чтобы минимизировалось число логических сложений, умножений или отрицаний, что важно для экономного конструирования ЭВМ.
Для двух переменных: Для трех переменных:
a 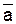 a
a 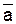
 | |||||||
 | |||||||
 | |||||||
 | |||||||
c
 | |||
 |
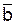 b
b 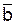

 |
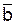 b
b 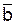
Для четырех переменных:
a 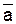
 | |||
 |
c 
 |
cd


 d
d

 |
 b
b 
Пример. Для логической функции заданной таблицей
| x1 | x2 | x3 | f |
построить карту Карно и на ее основе минимизировать функцию.
Решение. Построим карту согласно описанным выше правилам.
x1 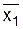









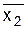 1 1 f = x1 v x2 & x3
1 1 f = x1 v x2 & x3
 |
x2 1 1 1
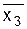 x3
x3 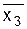
Рассмотрим пример представления простейшей функции картой Карно:
a 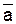
 | |||
 |
c 1 1 
 |
c 1 1 d


 f = b
f = b
 1 1 d
1 1 d
 1 1
1 1 
 |  |
 b
b 
|
|
|
|
|
Дата добавления: 2014-12-16; Просмотров: 442; Нарушение авторских прав?; Мы поможем в написании вашей работы!