Розгортка кривих поверхонь

Розгортка циліндричної поверхні в загальному випадку може бути побудована за принципом розгортання поверхні призми.

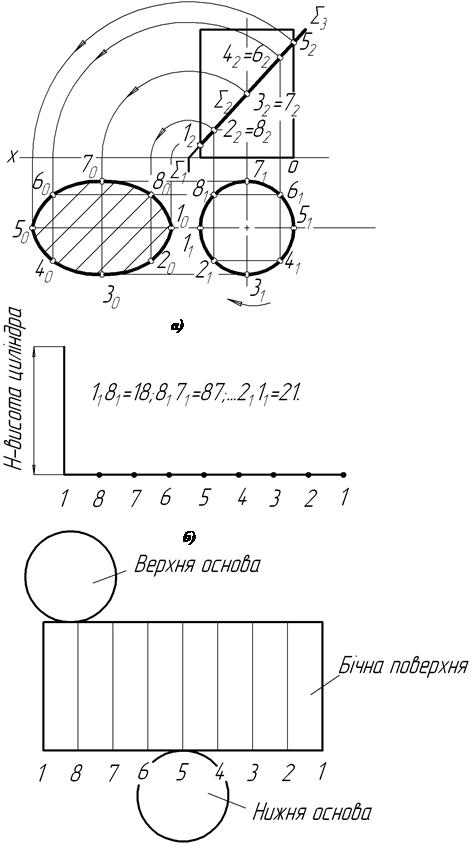
Задача 1. Побудувати розгортку нижньої частини циліндра, зрізаної фронтально-проекційною площиною S (рис7.35).

На рисунку 7.35а зображено в ортогональних проекціях циліндр, перерізаний фронтально-проекційною площиною S. На рисунку 7.35б,в,г,д – показано побудову розгортки зрізаної частини циліндра в поетапній побудові.

Для побудови розгортки поверхні зрізаного циліндра, спочатку треба побудувати повну розгортку циліндра. Для цього розгортку кола основи циліндра (відрізок прямий) розділимо на стільки рівних частин, на скільки буде розділено коло (рис.7.35б).

На рисунку 7.35в показана повна розгортка циліндра. Бічна поверхня циліндра зображена прямокутником з основою, рівною 2p і висотою, рівною висоті циліндра. Оскільки твірні циліндра паралельні площині p₂, то відомі всі відрізки твірних до лінії перерізу. Їх можна відкласти на розгортці від основи циліндра 11₀; 88₀;...; 11₀. З’єднавши точки названих відрізків плавною кривою, дістанемо розгортку еліпса – контур перерізу (рис.7.35г).

До розгортки бічної поверхні зрізаного циліндра приєднаємо дійсну величину фігури перерізу і коло (нижню основу циліндра) (рис.7.35д).

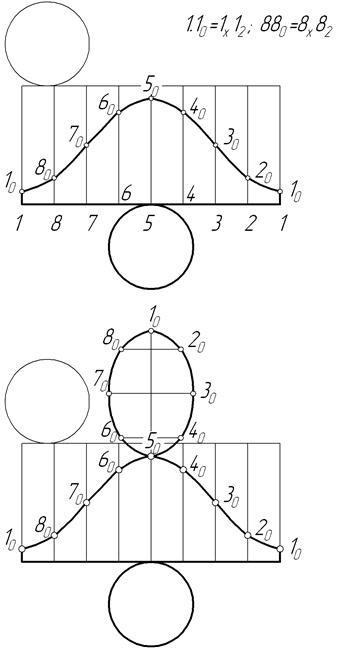
Якщо побудову розгортки почати не з найкоротшої твірної зрізаного циліндра, а з найбільшої, то розгортка зрізаного циліндра матиме такий вигляд, як на рисунку 7.36. Це дасть значну економію матеріалу при розкрої.

Побудова розгортки конічної поверхні в загальному випадку зводиться до принципу розгортання піраміди.

		в)
		Рисунок 7.35
		г)
		Продовження рисунку 7.29
		д)

Задача 2. Побудувати розгортку нижньої частини конуса, зрізаної фронтально-проекційною площиною S (рис.7.37).

На рисунку 7.37а зображено в ортогональних проекціях конус, перетнутий фронтально-проекційною площиною S.

На рисунку 7.37б,в,г,д показано побудову розгортки зрізаної частини конуса в поетапній побудові. На рисунку 7.37б показано перший крок побудови розгортки. Для цього розгортку кола основи конуса (дуга зроблена радіусом, що дорівнює крайній твірній конуса) розділимо на стільки частин, на скільки було розділено коло – основа конуса на p₁. На рисунку 7.37б показано розгортку бічної поверхні конуса – це сектор, радіусом якого є бічна твірна конуса і дуга, яку стягують хорди, що рівні поділу кола основи конуса.

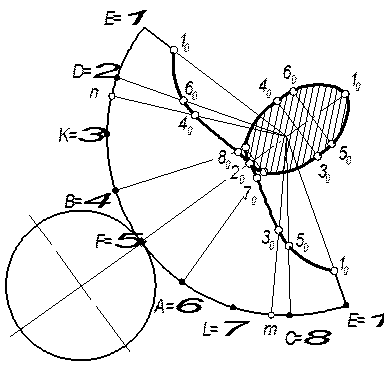
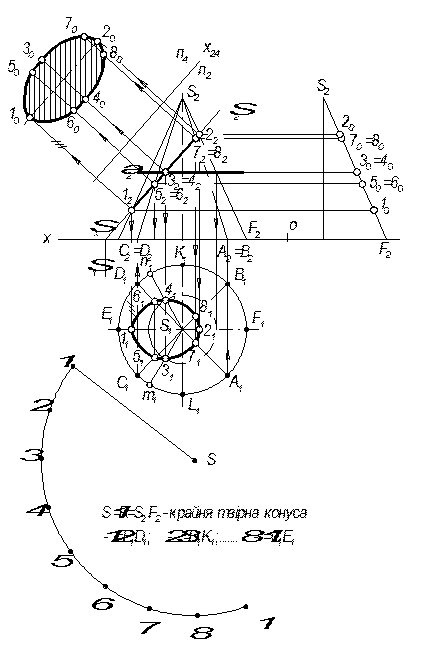Розгортку бічного контура перетину конуса площиною (рис.7.37г) одержано в результаті відкладання від вершини сектора (або від лінії основи) відрізків, які дорівнюють дійсним відстаням від вершини конуса до точки перетину твірних з площиною S (знаходження дійсної величини відрізка показані на рисунку 7.37,а шляхом витягування кожної із точок 5, 6, 3, 4, 7, 8 на крайню твірну) або, інакше кажучи – це спосіб обертання, розглянутий у розділі 5. Отже, S₂2₀; S₂7₀;...; S₂1₀ – це дійсна величина шуканих відрізків. З’єднавши точки 1₀; 6₀; 4₀; і т.д. плавною кривою, дістанемо розгортку еліпса – контуру перерізу (рис.7.37г). Доповнивши розгортку бічної поверхні еліпсом (дійсна величина фігури перерізу) і основою конуса, дістанемо розгортку повної поверхні зрізаного конуса (рис.7.37д).

		а)
		д)

	Продовження рисунка 7.37

Дата добавления: 2014-12-16