
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Примеры заданий
|
|
|
|
Иррациональные неравенства
Помните! Начинать решение иррациональных неравенств нужно с нахождения области определения.
Пример 6. Решить неравенство 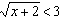 .
.
Решение:
Область определения: 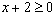 .
.
Так как арифметический корень не может быть отрицательным числом, то  .
.
Ответ: 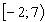 .
.
Пример 7. Найти все целые решения неравенства  .
.
Решение:
Область определения 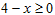 .
.
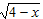 – быть отрицательным не может, следовательно, чтобы произведение было неотрицательным достаточно потребовать выполнения неравенства
– быть отрицательным не может, следовательно, чтобы произведение было неотрицательным достаточно потребовать выполнения неравенства 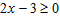 , при этом учитывая область определения. Т.е. исходное неравенство равносильно системе
, при этом учитывая область определения. Т.е. исходное неравенство равносильно системе 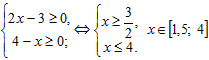 .
.
Целыми числами из этого отрезка будут 2; 3; 4.
Ответ: 2; 3; 4.
Решаем первое неравенство. Получаем
 .
.
Решаем второе неравенство. Получаем
 .
.
Отмечаем корни на координатной прямой и заштриховываем промежутки. Там, где промежутки пересекутся, и будет искомое решение. Отв.2.
 Синус, косинус, тангенс, котангенс.
Синус – отношение противолежащего катета к гипотенузе.
Косинус – отношение прилежащего катета к гипотенузе.
Тангенс – отношение синуса к косинусу.
Котангенс – отношение косинуса к синусу.
Синус, косинус, тангенс, котангенс.
Синус – отношение противолежащего катета к гипотенузе.
Косинус – отношение прилежащего катета к гипотенузе.
Тангенс – отношение синуса к косинусу.
Котангенс – отношение косинуса к синусу.
 Сумма углов.
Треугольник: 180°.
Четырехугольник: 360°.
n – угольник: 180°(n-2).
Теоремы.
В прямоугольном треугольнике катет, лежащий напротив угла в 30°, равен половине гипотенузы.
В четырехугольнике сумма соседних углов равна 180°.
Диагонали параллелограмма делятся точкой пересечения пополам.
Если угол одного треугольника равен углу другого треугольника, то площади этих треугольников относятся как произведения сторон, заключающих равные углы.
Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.
Векторы.
Сложение векторов
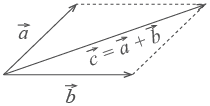
1. Правило параллелограмма. Чтобы сложить векторы
Сумма углов.
Треугольник: 180°.
Четырехугольник: 360°.
n – угольник: 180°(n-2).
Теоремы.
В прямоугольном треугольнике катет, лежащий напротив угла в 30°, равен половине гипотенузы.
В четырехугольнике сумма соседних углов равна 180°.
Диагонали параллелограмма делятся точкой пересечения пополам.
Если угол одного треугольника равен углу другого треугольника, то площади этих треугольников относятся как произведения сторон, заключающих равные углы.
Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.
Векторы.
Сложение векторов
1. Правило параллелограмма. Чтобы сложить векторы  и
и  , помещаем начала обоих в одну точку. Достраиваем до параллелограмма и из той же точки проводим диагональ параллелограмма. Это и будет сумма векторов
, помещаем начала обоих в одну точку. Достраиваем до параллелограмма и из той же точки проводим диагональ параллелограмма. Это и будет сумма векторов  и
и  .
.
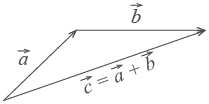
 2. Правило треугольника. Возьмем векторы
2. Правило треугольника. Возьмем векторы  и
и  . К концу первого вектора пристроим начало второго. Теперь соединим начало первого и конец второго. Это и есть сумма векторов
. К концу первого вектора пристроим начало второго. Теперь соединим начало первого и конец второго. Это и есть сумма векторов  и
и  .
.
 По тому же правилу можно сложить и несколько векторов. Пристраиваем их один за другим, а затем соединяем начало первого с концом последнего.
По тому же правилу можно сложить и несколько векторов. Пристраиваем их один за другим, а затем соединяем начало первого с концом последнего.
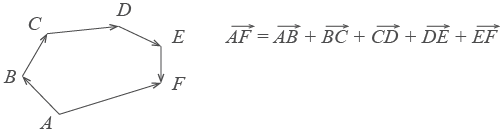 При сложении векторов
При сложении векторов  и
и 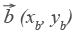 получаем:
получаем:
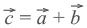
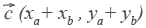 Вычитание векторов
Вектор
Вычитание векторов
Вектор 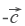 направлен противоположно вектору
направлен противоположно вектору 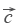 . Длины векторов
. Длины векторов 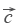 и
и 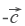 равны.
равны.
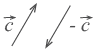 Разность векторов
Разность векторов  и
и 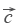 — это сумма вектора
— это сумма вектора  и вектора
и вектора  .
Углы.
.
Углы.
 Углы
Углы 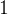 и
и 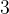
 вертикальные. Вертикальные углы равны, то есть
вертикальные. Вертикальные углы равны, то есть 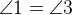
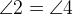 Углы
Углы 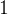 и
и 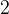
 смежные. Сумма смежных углов равна
смежные. Сумма смежных углов равна 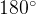 .
Углы
.
Углы 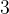 и
и 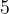
 накрест лежащие. Накрест лежащие углы равны.
накрест лежащие. Накрест лежащие углы равны.  ,
, 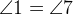 ,
,  ,
, 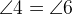 .
Углы
.
Углы 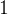 и
и 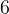
 односторонние. Они лежат по одну сторону от всей «конструкции». Сумма односторонних углов равна
односторонние. Они лежат по одну сторону от всей «конструкции». Сумма односторонних углов равна 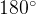 , то есть
, то есть 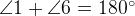 ,
,  .
Углы
.
Углы 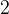 и
и 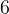 называются соответственными. Соответственные углы равны, то есть
называются соответственными. Соответственные углы равны, то есть 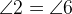 ,
, 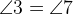 .
.
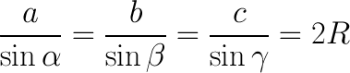 Теорема синусов.
Теорема синусов.
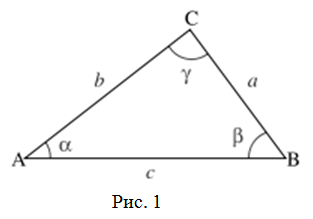 R – радиус окружности, описанной около рассматриваемого треугольника.
Теорема косинусов.
Квадрат любой стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на косинус угла между ними.
R – радиус окружности, описанной около рассматриваемого треугольника.
Теорема косинусов.
Квадрат любой стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на косинус угла между ними.
 Решение прямоугольных треугольников.
Стороны можно найти по следующим формулам:
Решение прямоугольных треугольников.
Стороны можно найти по следующим формулам:
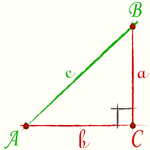 1. a= c ·sin(A)
2. b= c ·cos(A)
3. a= b ·tg(A)
4. b= c ·sin(B)
5. a= c ·cos(B)
6. b= a ·tg(B)
7.
1. a= c ·sin(A)
2. b= c ·cos(A)
3. a= b ·tg(A)
4. b= c ·sin(B)
5. a= c ·cos(B)
6. b= a ·tg(B)
7. 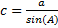 8.
8. 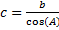 9.
9. 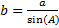 Теорема Пифагора.
Теорема Пифагора.
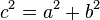 Окружность.
Вписанный угол измеряется половиной дуги, на которую он опирается.
Вписанная окружность.
В любой треугольник можно списать окружность.
В любом описанном четырехугольнике суммы противоположных сторон равны.
Если суммы противоположных сторон выпуклого четырехугольника равны, то в него можно вписать окружность.
Описанная окружность.
Около любого треугольника можно описать окружность.
В любом вписанном четырехугольнике сумма противоположных углов равна 180°.
Если сумма противоположных углов равна 180°, то около него можно описать окружность.
Средняя линия.
Средняя линия треугольника параллельна и равна половине основания.
Окружность.
Вписанный угол измеряется половиной дуги, на которую он опирается.
Вписанная окружность.
В любой треугольник можно списать окружность.
В любом описанном четырехугольнике суммы противоположных сторон равны.
Если суммы противоположных сторон выпуклого четырехугольника равны, то в него можно вписать окружность.
Описанная окружность.
Около любого треугольника можно описать окружность.
В любом вписанном четырехугольнике сумма противоположных углов равна 180°.
Если сумма противоположных углов равна 180°, то около него можно описать окружность.
Средняя линия.
Средняя линия треугольника параллельна и равна половине основания.
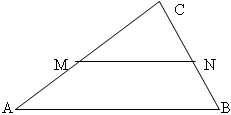 AM = MC и BN = NC =>
MN || AB
MN = AB/2
Средняя линия трапеции равна полусумме ее оснований.
AM = MC и BN = NC =>
MN || AB
MN = AB/2
Средняя линия трапеции равна полусумме ее оснований.
 MN || AB || DC AM = MD; BN = NC
MN средняя линия, AB и CD - основания, AD и BC - боковые стороны
MN = (AB + DC)/2
MN || AB || DC AM = MD; BN = NC
MN средняя линия, AB и CD - основания, AD и BC - боковые стороны
MN = (AB + DC)/2
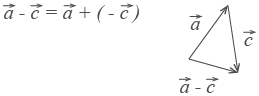 Умножение вектора на число
При умножении вектора
Умножение вектора на число
При умножении вектора  на число k получается вектор, длина которого в k раз отличается от длины
на число k получается вектор, длина которого в k раз отличается от длины  . Он сонаправлен с вектором
. Он сонаправлен с вектором  , если k больше нуля, и направлен противоположно
, если k больше нуля, и направлен противоположно  , если k меньше нуля.
, если k меньше нуля.
 Скалярное произведение векторов
Скалярным произведением векторов называется произведение длин векторов на косинус угла между ними.
Скалярное произведение векторов
Скалярным произведением векторов называется произведение длин векторов на косинус угла между ними.
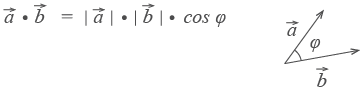 Скалярное произведение есть число.
Если векторы перпендикулярны, их скалярное произведение равно нулю. Скалярное произведение через координаты векторов
Скалярное произведение есть число.
Если векторы перпендикулярны, их скалярное произведение равно нулю. Скалярное произведение через координаты векторов  и
и  :
:
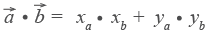 Угол между векторами:
Угол между векторами:
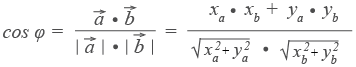 Длина вектора.
Длина вектора.
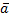 = { ax; ay }
|
= { ax; ay }
| 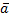 |=
|=  Координаты середины отрезка.
A(
Координаты середины отрезка.
A(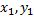 ) B(
) B( ) C(
) C(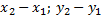 )
Биссектриса, медиана, высота.
Медиана – это отрезок, соединяющий вершину треугольника с серединой противоположной стороны. Любой треугольник имеет три медианы, которые пересекаются в одной точке:
)
Биссектриса, медиана, высота.
Медиана – это отрезок, соединяющий вершину треугольника с серединой противоположной стороны. Любой треугольник имеет три медианы, которые пересекаются в одной точке:
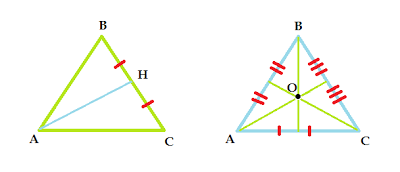 Биссектриса – это отрезок, делящий угл треугольника на две равные части. Любой треугольник имеет три биссектрисы, которые пересекаются в одной точке:
Биссектриса – это отрезок, делящий угл треугольника на две равные части. Любой треугольник имеет три биссектрисы, которые пересекаются в одной точке:  Высота – это перпендикуляр, проведённый из вершины треугольника к прямой, содержащей противоположную сторону. Любой треугольник имеет три высоты, которые пересекаются в одной точке:
Высота – это перпендикуляр, проведённый из вершины треугольника к прямой, содержащей противоположную сторону. Любой треугольник имеет три высоты, которые пересекаются в одной точке: 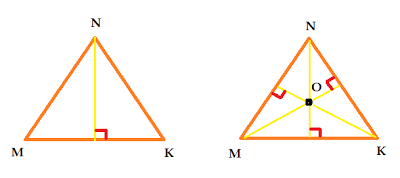
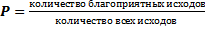 .
Если нужно найти вероятность того, что какое событие не случится, то нужно воспользоваться следующей формулой: 1 – P.
В нашем случае событием является выбор пирожка с яблоками, значит,
P =
.
Если нужно найти вероятность того, что какое событие не случится, то нужно воспользоваться следующей формулой: 1 – P.
В нашем случае событием является выбор пирожка с яблоками, значит,
P =  .
Другие задачи из теории вероятности.
Монета брошена два раза. Какова вероятность выпадения одного «орла» и одной «решки»?
Решение:
При бросании одной монеты возможны два исхода –
«орёл» или «решка».
При бросании двух монет – 4 исхода (2*2=4):
«орёл» - «решка»
«решка» - «решка»
«решка» - «орёл»
«орёл» - «орёл»
Один «орёл» и одна «решка» выпадут в двух случаях из четырёх. Р(А)=2:4=0,5.
Ответ: 0,5.
На экзамене 50 билетов, Руслан не выучил 5 из них. Найдите вероятность того, что ему попадется выученный билет.
Решение.
Руслан выучил 45 билетов.
Р(А)=45:50=0,9.
Ответ: 0,9.
Конкурс исполнителей проводится в 5 дней. Всего заявлено 75 выступлений — по одному от каждой страны. В первый день 27 выступлений, остальные распределены поровну между оставшимися днями. Порядок выступлений определяется жеребьёвкой. Какова вероятность, что выступление представителя России состоится в третий день конкурса?
Решение.
Всего исходов – 75.
Исполнители из России выступают
на третий день.
Благоприятных исходов – (75-27):4=12.
Р(А)=12: 75 = 0,16.
Ответ: 0,16.
Коля выбирает двузначное число. Найдите вероятность того, что оно делится на 5.
Решение.
Двузначные числа: 10;11;12;…;99.
Всего исходов – 90.
Числа, делящиеся на 5:
10,15,20,25,…,90,95.
Благоприятных исходов – 18.
Р(А)=18:90=0,2.
Ответ: 0,2.
Фабрика выпускает сумки. В среднем на 170 качественных сумок приходится шесть сумок со скрытыми дефектами. Найдите вероятность того, что купленная сумка окажется качественной. Результат округлите до сотых.
Решение.
Всего исходов – 176.
Благоприятных исходов – 170.
Р(А)=170:176 ≈ 0,97.
Ответ. 0,97.
.
Другие задачи из теории вероятности.
Монета брошена два раза. Какова вероятность выпадения одного «орла» и одной «решки»?
Решение:
При бросании одной монеты возможны два исхода –
«орёл» или «решка».
При бросании двух монет – 4 исхода (2*2=4):
«орёл» - «решка»
«решка» - «решка»
«решка» - «орёл»
«орёл» - «орёл»
Один «орёл» и одна «решка» выпадут в двух случаях из четырёх. Р(А)=2:4=0,5.
Ответ: 0,5.
На экзамене 50 билетов, Руслан не выучил 5 из них. Найдите вероятность того, что ему попадется выученный билет.
Решение.
Руслан выучил 45 билетов.
Р(А)=45:50=0,9.
Ответ: 0,9.
Конкурс исполнителей проводится в 5 дней. Всего заявлено 75 выступлений — по одному от каждой страны. В первый день 27 выступлений, остальные распределены поровну между оставшимися днями. Порядок выступлений определяется жеребьёвкой. Какова вероятность, что выступление представителя России состоится в третий день конкурса?
Решение.
Всего исходов – 75.
Исполнители из России выступают
на третий день.
Благоприятных исходов – (75-27):4=12.
Р(А)=12: 75 = 0,16.
Ответ: 0,16.
Коля выбирает двузначное число. Найдите вероятность того, что оно делится на 5.
Решение.
Двузначные числа: 10;11;12;…;99.
Всего исходов – 90.
Числа, делящиеся на 5:
10,15,20,25,…,90,95.
Благоприятных исходов – 18.
Р(А)=18:90=0,2.
Ответ: 0,2.
Фабрика выпускает сумки. В среднем на 170 качественных сумок приходится шесть сумок со скрытыми дефектами. Найдите вероятность того, что купленная сумка окажется качественной. Результат округлите до сотых.
Решение.
Всего исходов – 176.
Благоприятных исходов – 170.
Р(А)=170:176 ≈ 0,97.
Ответ. 0,97.
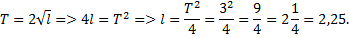 Ответ: 2,25.
На этом заданиях первой части ОГЭ заканчиваются.
За каждое задание первой части возможно получить 1 балл, т.е. при максимально правильном выполнении возможно набрать 20 баллов и получить «хорошо», даже не приступая к решению 2 части. Но помните, чтобы преодолеть минимальный порог, необходимо набрать не менее 8 баллов, решив как минимум 3 задания из блока «Алгебра» и по 2 задания из блоков «Геометрия» и «Реальная математика».
Удачи!
Теория для решения задач из второй части модуля «Алгебра».
Ответ: 2,25.
На этом заданиях первой части ОГЭ заканчиваются.
За каждое задание первой части возможно получить 1 балл, т.е. при максимально правильном выполнении возможно набрать 20 баллов и получить «хорошо», даже не приступая к решению 2 части. Но помните, чтобы преодолеть минимальный порог, необходимо набрать не менее 8 баллов, решив как минимум 3 задания из блока «Алгебра» и по 2 задания из блоков «Геометрия» и «Реальная математика».
Удачи!
Теория для решения задач из второй части модуля «Алгебра».
 V по теч. = Vсоб. + Vтеч.
Vпр. теч = Vсоб. – Vтеч.
Vсоб. = (Vпо теч. + Vпр. теч.): 2
Vтеч. = (Vпо теч. – Vпр. теч.): 2
V по теч. = Vсоб. + Vтеч.
Vпр. теч = Vсоб. – Vтеч.
Vсоб. = (Vпо теч. + Vпр. теч.): 2
Vтеч. = (Vпо теч. – Vпр. теч.): 2