
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Типы уравнений и способы их решения
|
|
|
|
Логарифмические уравнения
III уровень
II уровень
I уровень
1.1. Установить, имеет ли уравнение корни:
1) 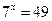 ; 2)
; 2) 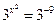 ;
;
3) 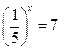 ; 4)
; 4) 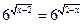 ;
;
5) 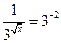 ; 6)
; 6) 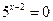 ;
;
7) 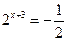 .
.
1.2. Определите, сколько корней имеет уравнение 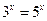 . Как это можно установить графически?
. Как это можно установить графически?
1.3. Решите уравнения:
1) 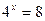 ; 2)
; 2)  ;
;
3) 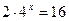 ; 4)
; 4) 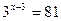 ;
;
5) 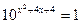 ; 6)
; 6) 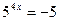 ;
;
7) 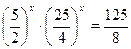 ; 8)
; 8)  ;
;
9) 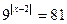 ; 10)
; 10) 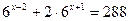 ;
;
11) 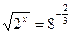 ; 12)
; 12) 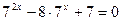 ;
;
13) 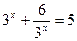 .
.
2.1. Решите уравнение:
1) 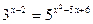 ;
;
2) 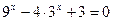 ;
;
3) 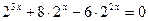 ;
;
4) 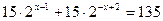 ;
;
5) 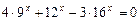 ;
;
6) 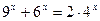 ;
;
7) 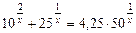 ;
;
8) 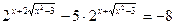 ;
;
9) 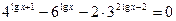 ;
;
10) 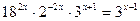 ;
;
11) 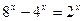 ;
;
12) 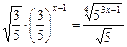 ;
;
13) 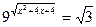 ;
;
14) 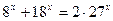 ;
;
2.2. Найдите значение выражения 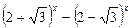 , если
, если 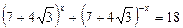 .
.
3.1. Решите уравнение:
1) 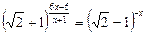 ;
;
2) 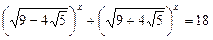 ;
;
3) 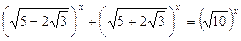 ;
;
4) 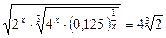 ;
;
5) 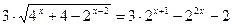 ;
;
6) 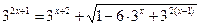 ;
;
7) 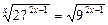 ;
;
8) 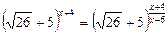 ;
;
9) 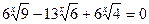 ;
;
10) 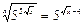 ;
;
11) 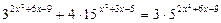 ;
;
12) 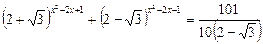 ;
;
13) 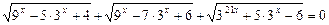 ;
;
14) 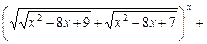
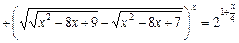 ;
;
15) 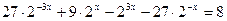 ;
;
16) 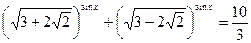 ;
;
17) 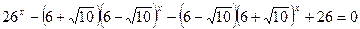 ;
;
3.2. Найдите сумму корней уравнения
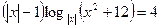 .
.
Логарифмическим уравнением называется уравнение, в котором неизвестная величина содержится под знаком логарифма или в его основании.
При решении логарифмических уравнений обязательно учитывается ОДЗ логарифма. Если ОДЗ найти сложно, то можно только выписать условия, а затем проверить полученные корни подстановкой в ОДЗ (можно проверять подстановкой в уравнение, не выписывая ОДЗ).
Всюду далее f(x), g(x), h(x) – некоторые выражения с переменной (число).
I тип:
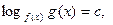 (8)
(8)
где c Î R.
ОДЗ: 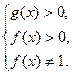
На указанной ОДЗ уравнение (8) решается по определению логарифма:
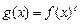 .
.
II тип:
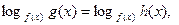 (9)
(9)
ОДЗ: 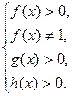
На основании равенства логарифмов, уравнение (9) сводится к равносильному ему (на указанной ОДЗ) уравнению:
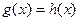 .
.
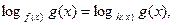 (10)
(10)
ОДЗ: 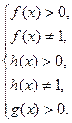
Данное уравнение на ОДЗ равносильно совокупности уравнений:
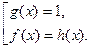
III тип: уравнения, решаемые заменой переменной
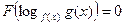 , (11)
, (11)
где F – некоторое выражение относительно 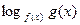 .
.
Необходимо определить ОДЗ уравнения, учитывая все условия существования логарифма и выражения F.
Далее заменяют 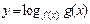 и решают уравнение
и решают уравнение 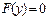 .
.
Если 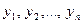 – корни последнего уравнения, то, после возвращения к старой переменной, необходимо решить совокупность
– корни последнего уравнения, то, после возвращения к старой переменной, необходимо решить совокупность
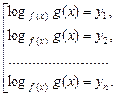
Полученные корни проверяют по ОДЗ.
Замечание. Если вместо какого-либо выражения f(x), g(x), h(x) уравнения (8) – (11) содержат число, то соответствующее условие не записывают в ОДЗ.
Пример 1. Решить уравнение 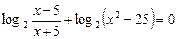 .
.
Решение. Находим ОДЗ:

Решение системы:
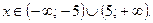
Преобразуем уравнение к виду
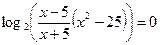 .
.
Получили уравнение I типа, которое решается по определению логарифма:
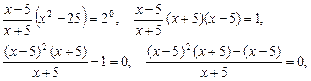
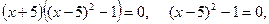 ,
, 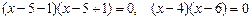 , откуда
, откуда  .
.
Из полученных значений корень  не подходит по ОДЗ.
не подходит по ОДЗ.
Получаем ответ: 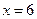 .
.
Пример 2. Решить уравнение 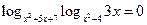 .
.
Решение. Записываем условия, определяющие ОДЗ:

Заданное уравнение относится к I типу. Получаем
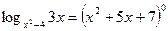 ,
, 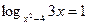 .
.
Снова используем определение логарифма
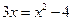 , т.е.
, т.е. 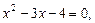 откуда
откуда 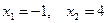 .
.
Полученные корни проверяем подстановкой в условия, определяющие ОДЗ уравнения. Убеждаемся, что корень 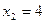 подходит, а корень
подходит, а корень 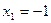 не подходит по ОДЗ.
не подходит по ОДЗ.
Получаем ответ:  .
.
Пример 3. Решить уравнение
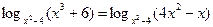 .
.
Решение. Записываем условия, определяющие ОДЗ:
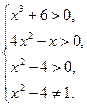
Данное уравнение относится ко II типу, т.е. решается по свойству равенства логарифмов. Получаем
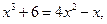 т.е.
т.е.  .
.
Раскладываем левую часть на множители:
 , откуда получаем
, откуда получаем 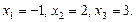
Подставляем найденные значения в ОДЗ, находим, что уравнение имеет только один корень 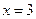 .
.
В ответе имеем: 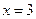 .
.
Пример 4. Решить уравнение
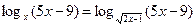 .
.
Решение. Находим ОДЗ:
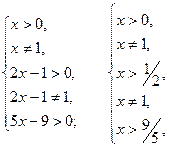 т.е.
т.е.  .
.
Данное уравнение относится ко II типу. Решаем совокупность:
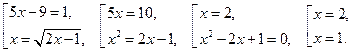
По ОДЗ подходит только корень 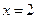 , т.к.
, т.к.  .
.
Получаем ответ: 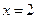 .
.
Пример 5. Решить уравнение 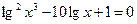 .
.
Решение. ОДЗ: 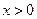 . Преобразуем уравнение:
. Преобразуем уравнение:
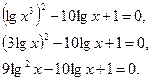
Имеем квадратное уравнение относительно 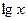 (уравнение III типа). Заменяем
(уравнение III типа). Заменяем 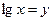 :
:
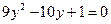 .
.
Решая полученное квадратное уравнение, находим корни 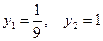 . Возвращаемся к переменной x:
. Возвращаемся к переменной x:
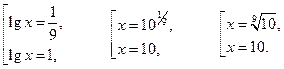
Оба корня подходят по ОДЗ, получаем ответ:  .
.
Пример 6. Решить уравнение
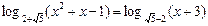 .
.
Решение. Запишем условия ОДЗ: 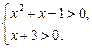
Воспользуемся тем, что
 . Тогда
. Тогда
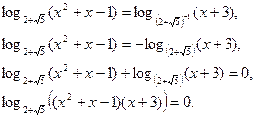
Решаем полученное уравнение как уравнение I типа:
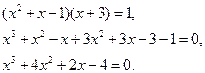
Среди целых делителей свободного члена находим корень 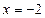 . Он подходит по ОДЗ.
. Он подходит по ОДЗ.
Пришли к ответу: 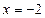 .
.
Пример 7. Решить уравнение 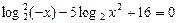 .
.
Решение. ОДЗ: 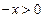 , т.е.
, т.е. 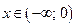 .
.
Воспользуемся свойствами модуля: 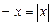 , если
, если 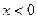 , и
, и  . Тогда уравнение перепишется в виде
. Тогда уравнение перепишется в виде
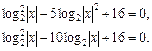
Заменяем 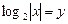 и приходим к квадратному уравнению
и приходим к квадратному уравнению
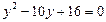 ,
,
корнями которого являются числа 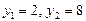 .
.
Возвращаемся к старой переменной:
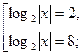
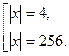
Раскрываем модуль, используя ОДЗ:
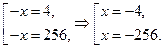
Получаем ответ: 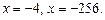
Пример 8. Решить уравнение
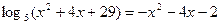 .
.
Решение. ОДЗ: 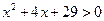 , т.е.
, т.е. 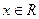 .
.
Рассмотрим левую часть уравнения:

Преобразуем правую часть. Получим
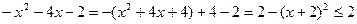 .
.
Используя функциональный метод решения, заключаем, что решением исходного уравнения является решение системы
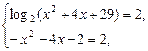
т.е. 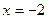 .
.
Получаем ответ: 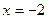 .
.
Пример 9. Найти сумму корней уравнения 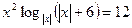 .
.
Решение. Для данного уравнения характерно следующее: если 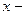 корень уравнения, то и
корень уравнения, то и 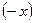 тоже корень уравнения. Поэтому если уравнение имеет корни, то их сумма будет равна нулю. Подстановкой находим корни
тоже корень уравнения. Поэтому если уравнение имеет корни, то их сумма будет равна нулю. Подстановкой находим корни 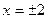 .
.
Получаем ответ: 0.
Задания
|
|
|
|
|
Дата добавления: 2014-12-16; Просмотров: 2371; Нарушение авторских прав?; Мы поможем в написании вашей работы!