Типы неравенств и способы их решения

Всюду далее некоторые выражения с переменой.

I тип:

, (16)

где a > 0.

1.Если 0 < a < 1, то неравенство (16) равносильно системе

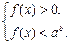(17)

2.Если a > 1, то неравенство (16) равносильно системе

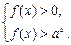
Заметим, что в этом случае первое неравенство системы (17) можно не решать, т.к. во втором неравенстве .

. (18)

Решение неравенства (18) сводится к решению совокупности двух систем:

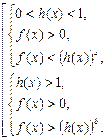
Неравенство 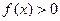во второй системе можно не решать, т.к. оно справедливо при выполнении двух других неравенств этой системы.

II тип:

, (19)

1. Если 0 < a < 1, то неравенство (19) равносильно системе

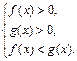(20)

Неравенство в системе (20) можно не решать, т.к. оно выполняется при условии выполнения двух других неравенств этой системы.

2. Если , то неравенство (19) равносильно системе

(21)

Неравенство 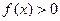в системе (21) можно не решать.

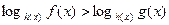(22)

Поскольку в основании содержится переменная величина, то в общем случае решение неравенства (22) зависит от величины основания по сравнению с числом 1. Поэтому решаем совокупность двух систем:

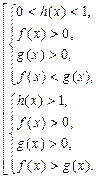
III тип:

, (23)

где F – некоторое выражение относительно .

Необходимо заменить и решить неравенство F(y) > 0. Полученные в качестве решения последнего неравенства промежутки записывают в виде неравенств относительно y, а затем возвращаются к старой переменной.

Аналогично решают неравенства I – III типов, в которых вместо знака «>» использованы знаки «³», «<», «£».

Пример 1. Решить неравенство .

Решение. Имеем неравенство I типа. Т.к. основание логарифма меньше числа 1, то решение неравенства сводится к решению системы

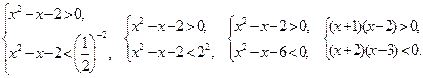Используем далее метод интервалов (рис.12)

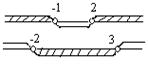
Рис.12

Получаем ответ: .

Пример 2. Решить неравенство .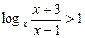

Решение. Данное неравенство относится к I типу. Поэтому решаем совокупность двух систем

Первая система решений не имеет. Решаем вторую систему

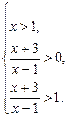
Второе неравенство этой системы не решаем, т.к. оно справедливо, если выполняется последнее неравенство. Получаем

Используем метод интервалов (рис.13).

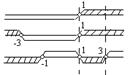
Рис.13

Получаем ответ: .

Пример 3. Решить неравенство .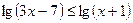

Решение. Это неравенство II типа, причем основание логарифма больше числа 1. Поэтому решаем систему

Получаем

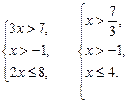
Подводя итог, приходим к ответу .

Пример 4. Решить неравенство

.

Решение. Имеем неравенство III типа.

Заменяем 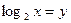и решаем кубическое неравенство

.

Разлагаем левую часть неравенства на множители:

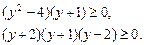
Используем далее метод интервалов (рис.14).

Рис.14

Получили решение . Записываем его в виде:

Возвращаемся к неизвестной x и с учетом ОДЗ заданного неравенства имеем:

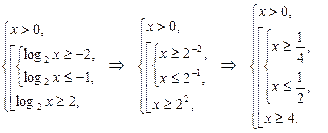
Получаем ответ .

Задания

Дата добавления: 2014-12-16