Релятивистский закон сложения скоростей

Преобразования Лоренца (вывод).

Основные постулаты специальной теории относительности. Интервал. Классификация интервалов.

Специальная теория относительности (СТО; также частная теория относительности) — теория, описывающая движение, законы механики и пространственно-временные отношения при произвольных скоростях движения, меньших скорости света в вакууме, в том числе близких к скорости света.

Постулат 1 (принцип относительности Эйнштейна). Любое физическое явление протекает одинаково во всех инерциальных системах отсчёта. Это означает, что форма зависимости физических законов от пространственно-временных координат должна быть одинаковой во всех ИСО, то есть законы инвариантны относительно переходов между ИСО. Принцип относительности устанавливает равноправие всех ИСО.

Учитывая второй закон Ньютона (или уравнения Эйлера-Лагранжа в лагранжевой механике), можно утверждать, что если скорость некоторого тела в данной ИСО постоянна (ускорение равно нулю), то она должна быть постоянна и во всех остальных ИСО. Иногда это и принимают за определение ИСО.

Постулат 2 (принцип постоянства скорости света). Скорость света в «покоящейся» системе отсчёта не зависит от скорости источника.

Принцип постоянства скорости света противоречит классической механике, а конкретно — закону сложения скоростей. При выводе последнего используется только принцип относительности Галилея и неявное допущение одинаковости времени во всех ИСО. Таким образом, из справедливости второго постулата следует, что время должно быть относительным — неодинаковым в разных ИСО. Необходимым образом отсюда следует и то, что «расстояния» также должны быть относительны. В самом деле, если свет проходит расстояние между двумя точками за некоторое время, а в другой системе — за другое время и притом с той же скоростью, то отсюда непосредственно следует, что и расстояние в этой системе должно отличаться.

Второй постулат следует формулировать как существование предельной (максимальной) скорости движения. По своей сути она должна быть одинаковой во всех ИСО, хотя бы потому, что в противном случае различные ИСО не будут равноправны, что противоречит принципу относительности. Более того, исходя из принципа «минимальности» аксиом, можно сформулировать второй постулат просто как существование некоторой скорости, одинаковой во всех ИСО, а после вывода соответствующих преобразований — показать, что это предельная скорость

Интервалом между произвольными событиями называется квадратный корень следующей величины:

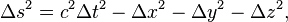
где 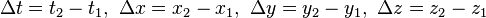— являются разностями времён и координат двух событий.

Непосредственной подстановкой преобразований Лоренца можно убедиться, что интервал оказывается одинаковым во всех ИСО. Этот факт однако, можно показать и без использования полученных преобразований Лоренца, а используя только постулаты СТО (включая однородность и изотропность пространства и однородность времени).

Существует множество способов вывода преобразований Лоренца. Рассмотрим один из вариантов.

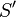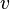Предполагается, что начало координат системы (в силу однородности пространства это может быть любая покоящаяся в этой системе точка) движется относительно системы со скоростью . Соответственно, начало координат (покоящаяся точка) системы движется в 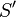со скоростью 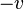. В целях упрощения дальнейшего изложения (а также самих конечных формул преобразования) будем исходить из предположения о совпадении начал отсчета обоих ИСО (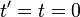, когда 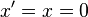) и одинаковой ориентированности координатных осей таким образом, чтобы относительное движение ИСО было направлено вдоль оси 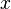(с противоположными знаками в разных системах). При относительном движении систем вдоль оси x можно считать, что 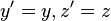(это можно также показать более строго), таким образом, фактически можно рассматривать преобразования для одномерного пространства и рассматривать только векторы двумерного пространства-времени .

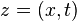В силу однородности пространства и времени и изотропности пространства и принципа относительности преобразования от одной ИСО к другой должны быть линейными^[14][15]. Линейность преобразований можно также вывести предполагая, что, если два объекта имеют одинаковые скорости относительно одной ИСО, то их скорости будут равны и в любой другой ИСО,^[16] (при этом необходимо использовать также слабые предположения о дифференцируемости и взаимной однозначности функций преобразования). Если использовать только «определение» ИСО: если некоторое тело имеет постоянную скорость относительно одной инерциальной системы отсчёта, то его скорость будет постоянна и относительно любой другой ИСО, то можно показать только, что преобразования между двумя ИСО должны быть дробно-линейными функциями координат и времени с одинаковым знаменателем ^{[10] [17]}.

Таким образом, если 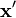— пространственно-временной вектор в системе 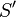, а 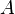-матрица искомого линейного преобразования, то 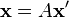. Матрица преобразования может зависеть только от относительной скорости рассматриваемых ИСО, то есть . Исходя только из соглашений об относительной скорости движения систем отсчета можно установить общий вид (структуру) линейного преобразования и закона сложения скоростей:

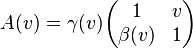и закон сложения скоростей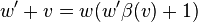

Пусть в системе отсчета K’ материальная точка движется вдоль оси х’ спостоянной скоростью Система K’ движется относительно системы K в том же направлении со скоростью v, Определим, чему равна скорость материальной точки v_o, относительно системы K, т.е. чему равно 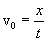. Пусть при 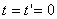м.т. находится в начале координат, причем 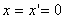. Для системы K:

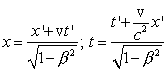
Подставляя 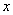и t в формулу для v_o

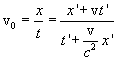
Делим числитель и знаменатель на t

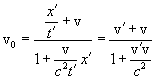
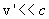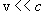Это равенство выражает собой релятивистский закон сложения скоростей. При малых значениях скоростей и имеем

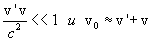
т.е. релятивистский закон сложения скоростей переходит в классический

Дата добавления: 2014-12-16