Основные законы и формулы

Дополнительная

6 Волькенштейн, В.С. Сборник задач по общему курсу физики / В.С. Волькенштейн. – М.: Наука, 1985. – 381 с.

7 Калашников, С.Г. Электричество / С.Г. Калашников. – М.: Высшая школа, 1964. – 668 с.

8 Матвеев, А.Н. Электричество и магнетизм / А.Н. Матвеев. – М.: Высшая школа, 1983. – 463 с.

9 Иродов, И.Е. Задачи по общей физике / И.Е. Иродов. – М.: Наука, 1988. – 416 с.

10 Савельев, И.В. Сборник задач и вопросов по общей физике / И.В. Савельев. - М.: Наука, 1988. – 288 с.

11 Чертов, А.Г. Физические величины / А.Г. Чертов. – М.: Высшая школа, 1990. – 315 с.

12 Сена, Л.И. Единицы физических величин и их размерности / Л.И. Сена. - М.: Наука, 1988. – 432 с.

13 Физика: задания к практическим занятиям / под ред.
Ж.П. Лагутиной. – Минск: Вышэйшая школа, 1989. – 236 с.

14 Сборник задач по физике / под ред. М.С. Цедрика. – Минск: Вышэйшая школа, 1976. – 320 с.

15 Фирганг, Е.В. Руководство к решению задач по курсу общей физики / Е.В. Фирганг. – М.: Высшая школа, 1977. – 351 с.

16 Кухлинг, Х. Справочник по физике / Х. Кухлинг. – М.: Мир, 1985. – 520 с.

17 Детлаф, А.А. Справочник по физике / Б.М. Яворский,

18 Зильберман, Г.Е. Электричество и магнетизм / Г.Е. Зильбер- ман. – М.: Наука, 1970. – 384 с.

19 Новодворская, Е.М. Методика проведения упражнений по физике во втузе / Е.М. Новодворская, Э.М. Дмитриев. – М.: Высшая школа, 1981. – 318 с.

20 Сборник задач по общему курсу физики / под ред. А.Н. Куценко и Ю.В. Рублева. – М.: Высшая школа, 1972. - 432 с.

Закон Кулона (для однородной изотропной среды)

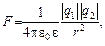
где F - сила электрического взаимодействия точечных зарядов q ₁ и q ₂;
e₀ = 8,85 ∙10^-12 Ф/м - электрическая постоянная; e - диэлектрическая проницаемость среды; r - расстояние между зарядами.

Закон сохранения электрического заряда

,

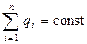где 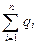- алгебраическая сумма зарядов, входящих в электрически изолированную систему; n - число зарядов.

Напряжённость электрического поля

,

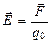где 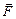- сила, действующая на точечный положительный заряд q ₀, помещённый в данную точку поля.

Поток вектора напряжённости электрического поля:

а) через произвольную поверхность, помещённую в неоднородное поле,

,

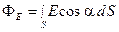где a - угол между вектором напряжённости поля и нормалью к элементу поверхности; dS – площадь элемента поверхности;

б) через плоскую поверхность S, помещённую в однородное электрическое поле,

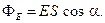
Поток вектора напряжённости электрического поля через замкнутую поверхность S

,

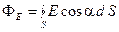где интегрирование ведётся по всей поверхности.

Теорема Остроградского-Гаусса для электростатического поля в вакууме. Поток вектора напряжённости через произвольную замкнутую поверхность, охватывающую электрические заряды
q ₁, q ₂, q_{n ,}

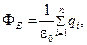
где 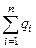- алгебраическая сумма зарядов, заключённых внутри этой замкнутой поверхности; n - число зарядов.

Напряжённость поля, создаваемого точечным зарядом q на расстоянии r от заряда,

.

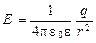Напряжённость поля, создаваемого равномерно заряженной сферической поверхностью радиусом R и зарядом q на расстоянии r от центра сферы:

а) внутри сферы (r < R)

Е = 0;

б) на поверхности сферы (r = R)

;

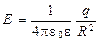в) вне сферы (r > R)

.

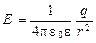Принцип суперпозиции (наложения) электрических полей, согласно которому напряжённость результирующего поля, созданного двумя и более источниками поля, равна векторной сумме напряжённостей складываемых полей:

.

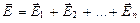В случае двух электрических полей с напряжённостям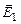и и 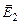модуль вектора напряжённости

,

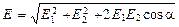где a - угол между векторам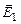и и .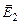

Поверхностная плотность заряда

.

Напряжённость поля, создаваемого бесконечной равномерно заряженной плоскостью,

.

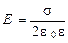Напряжённость поля, создаваемого двумя параллельными бесконечными равномерно и разноимённо заряженными плоскостями, с одинаковой по модулю поверхностной плотностью заряда (поле плоского конденсатора)

.

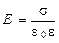Линейная плотность t заряда есть величина, равная отношению заряда, распределённого по нити, к длине нити (цилиндра):

.

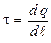Напряжённость поля, создаваемого бесконечно длинной равномерно заряженной нитью (или цилиндром) на расстоянии r от оси:

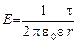
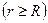; E = 0 (r ≤ R).

Напряжённость поля, создаваемого объемно заряженным шаром,

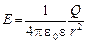
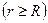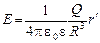; (r ≤ R).

Циркуляция вектора напряжённости электрического поля есть величина, численно равная работе по перемещению единичного точечного положительного заряда вдоль любого замкнутого контура. Циркуляция выражается интегралом и в случае электростатического поля равна нулю:

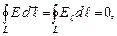
где 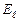- проекция вектора напряжённости в данной точке контура на направление касательной к контуру в той же точке.

Потенциал электрического поля есть величина, равная отношению потенциальной энергии точечного положительного заряда, помещённого в данную точку поля, к этому заряду:

.

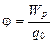Потенциал электрического поля есть величина, равная отношению работы силы по перемещению точечного положительного заряда из данной точки в бесконечность к величине этого заряда:

.

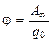Потенциал электрического поля в бесконечности от источника поля условно принимается равным нулю.

Потенциал электрического поля, создаваемый точечным зарядом q на расстоянии r от заряда:

.

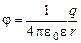Потенциал электрического поля, создаваемого равномерно заряженной сферической поверхностью радиусом R и зарядом q на расстоянии r от центра сферы:

а) внутри сферы (r < R)

;

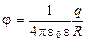б) на поверхности сферы (r = R)

;

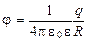в) вне сферы (r > R)

.

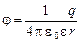Во всех приведенных формулах для потенциала сферы e есть диэлектрическая проницаемость однородного диэлектрика, окружающего сферу.

Потенциал электрического поля, созданного системой зарядов, в данной точке согласно принципу суперпозиции равен алгебраической сумме потенциалов, создаваемых отдельными зарядами q ₁, q ₂, ..., q_n:

.

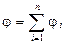Энергия взаимодействия системы точечных зарядов

,

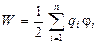где j _i - потенциал, создаваемый в той точке, где находится заряд q_i, всеми зарядами, кроме i -го.

Связь между напряжённостью и потенциалом электростатического поля

.

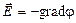В случае электрического поля, обладающего центральной или сферической симметрией, эта связь выражается формулой

.

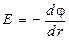Для однородного поля, т.е. поля, напряжённость которого в каждой его точке одинакова по модулю и направлению,

,

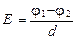где j₁ и j₂ - потенциалы точек двух эквипотенциальных поверхностей; d - расстояние между этими поверхностями вдоль силовой линии.

Работа, совершаемая силами электрического поля при перемещении точечного заряда q из точки 1 в точку 2,

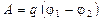, или ,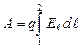

где 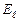- проекция вектора напряжённости на направление перемещения; 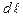- модуль перемещения.

В случае однородного поля формула для работы принимает вид

,

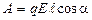где 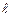- модуль перемещения; a - угол между направлениями векторов напряженности и перемещения.

Диполь есть система двух равных по величине и противоположных по знаку точечных электрических зарядов, расстояние между которыми значительно меньше расстояния от центра диполя до точек наблюдения. Вектор 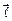, проведённый от отрицательного заряда диполя к его положительному заряду, называется плечом диполя.

Электрический момент диполя

.

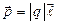Напряжённость и потенциал поля диполя в точке, лежащей на оси диполя,

где e - диэлектрическая проницаемость среды; r - модуль радиус-вектора, проведённого от центра диполя к рассматриваемой точке поля.

Напряжённость и потенциал поля диполя в точке, лежащей на перпендикуляре к плечу диполя, восстановленном из его середины,

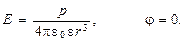
Механический момент, действующий на диполь в однородном электрическом поле,

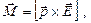или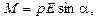

где a - угол между направлениями векторов дипольного момента и напряжённости поля.

Вектор поляризации или поляризованность

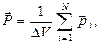
где 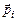- электрический момент i -й молекулы; N - число молекул, содержащихся в объёме D V.

Связь поляризованности с напряжённостью поля в диэлектрике

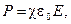
где c - диэлектрическая восприимчивость диэлектрика.

Связь диэлектрической проницаемости с диэлектрической восприимчивостью

.

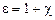Напряжённость среднего макроскопического поля в диэлектрике связана с напряжённостью Е ₀ внешнего поля соотношениями:

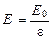или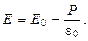

Электрическое смещение связано с напряжённостью поля соотношением

.

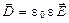Теорема Остроградского-Гаусса для электростатического поля в веществе. Поток вектора электрического смещения через произвольную замкнутую поверхность, охватывающую заряды q ₁, q ₂ ,... q_n,

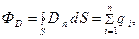
где D_n - проекция вектора электрического смещения на направление нормали к элементу поверхности; 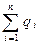- алгебраическая сумма свободных зарядов, заключённых внутри замкнутой поверхности;
n - число зарядов.

Электрическая ёмкость уединённого проводника или конденсатора ,

где D q - заряд, сообщённый проводнику (конденсатору); Dj - изменение потенциала, вызванное этим зарядом.

Емкость уединённой проводящей сферы радиусом R, находящейся в среде с диэлектрической проницаемостью e,

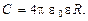
Электрическая ёмкость плоского конденсатора

,

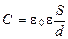где S - площадь пластины; d - расстояние между пластинами.

Электрическая ёмкость цилиндрического конденсатора

,

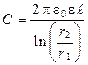где 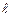- длина обкладок конденсатора; r ₁ и r ₂ - радиусы полых коаксиальных цилиндров.

Электрическая ёмкость сферического конденсатора

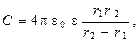
где r ₁ и r ₂ - радиусы концентрических сфер.

Емкость батареи конденсаторов при последовательном соединении:

а) в общем случае ;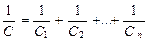

б) в случае двух конденсаторов .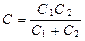

Емкость батареи конденсаторов при параллельном соединении

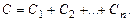
Сила притяжения пластин конденсатора

.

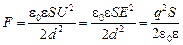Энергия заряженного конденсатора

.

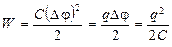Энергия электростатического поля плоского конденсатора

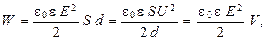
где S - площадь одной пластины; U - разность потенциалов между пластинами; V - объём конденсатора.

Объёмная плотность энергии

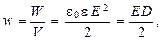
где Е - напряжённость электрического поля в среде с диэлектрической проницаемостью e; D - электрическое смещение.

Сила тока определяется количеством электричества, проходящим через поперечное сечение проводника в единицу времени,

.

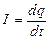Плотность тока есть векторная величина, измеряемая отношением силы тока к единице площади поперечного сечения проводника,

,

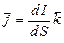где 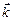- единичный вектор, совпадающий по направлению с направлением движения положительных зарядов.

Плотность тока в проводнике

,

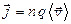где n - концентрация носителей заряда; 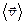- средняя скорость упорядоченного движения зарядов в проводнике.

Закон Ома:

а) для однородного участка цепи (т.е. не содержащего ЭДС)

;

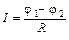б) для неоднородного участка цепи

;

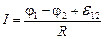в) для замкнутой цепи

,

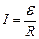где (j₁ - j₂) - разность потенциалов на концах участка цепи;
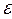₁₂- ЭДС источников тока, входящих в участок; R _о - сопротивление цепи (участка цепи), R _о = R + r; R – внешнее сопротивление; r –внутреннее сопротивление источника тока; 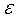- ЭДС всех источников тока цепи.

Закон Ома в дифференциальной форме: плотность тока пропорциональна напряжённости электрического поля в данной точке проводника:

,

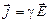где g = 1/r - удельная проводимость материала проводника.

Сопротивление однородного проводника

,

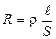где r - удельное сопротивление материала; 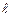- длина проводника; S - площадь поперечного сечения.

Зависимость удельного сопротивления от температуры

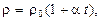
где r₀ и r - удельные сопротивления, соответственно, при 0 ⁰С и при температуре t (по шкале Цельсия); a - температурный коэффициент сопротивления.

Сопротивление проводников при последовательном и параллельном соединениях

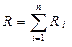и ,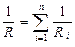

где n - число проводников; R_i - сопротивление i -го проводника.

Правила Кирхгофа для разветвлённых цепей:

1) алгебраическая сумма токов, сходящихся в любом узле, равна нулю:

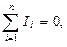
где n - число токов, сходящихся в узле;

2) для любого замкнутого контура алгебраическая сумма произведений сил токов на сопротивления соответствующих участков цепи равна алгебраической сумме всех ЭДС, действующих в этом контуре:

,

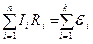где n - число участков, содержащих активное сопротивление; I_i - сила тока на i -м участке цепи; R_i - сопротивление i -го участка; k - число участков, содержащих источники тока; 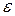_i - ЭДС источников тока на i -м участке.

Работа, совершаемая электростатическим полем и сторонними силами в участке цепи постоянного тока за время t,

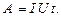
Мощность тока

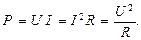
Закон Джоуля-Ленца определяется соотношением:

,

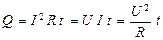где Q - количество теплоты, выделяющееся в участке цепи постоянного тока за время t. Закон Джоуля-Ленца справедлив при условии, что участок неподвижен и в нём не протекают химические реакции.

Закон Джоуля-Ленца в дифференциальной форме

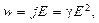
где w - удельная тепловая мощность тока, т.е. количество теплоты, выделяемое в единицу времени в единице объема проводника при протекании в нем тока.

Дата добавления: 2014-12-16