Расчет емкости и энергии заряженного конденсатора 1 страница

При расчете емкости и энергии плоского заряженного конденсатора особое значение имеют задачи, в которых рассматривается изменение энергии вследствие, например, удаления диэлектрика или раздвижения обкладок конденсатора. При этом, если конденсатор отключается от источника тока до проведения указанных действий, то заряд на его обкладках изменяться не будет и энергия конденсатора может меняться только за счет работы приложенных внешних сил. Поэтому возрастание энергии конденсатора однозначно соответствует положительной работе внешних сил.

Во втором случае, когда конденсатор не отключается от источника, на обкладках поддерживается постоянное напряжение. В этом случае изменение энергии конденсатора будет определяться работой внешних сил и работой сторонних сил источника по изменению заряда конденсатора.

Пример 8. Между обкладками плоского конденсатора, заряженного до разности потенциалов 1,5 кВ, зажата пластинка толщиной 5 мм из парафина ( e = 2). Определить поверхностную плотность связанных зарядов на парафине.

Д а н о: U = 1,5 кB, d = 5 мм, ε = 2 σ ' –?

Р е ш е н и е

Векторы электрического смещения 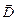и напряжённости электрического поля связаны между собой соотношением

,

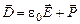где 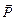- вектор поляризованности диэлектрика. Так как векторы 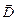и нормальны к поверхности диэлектрика, то D_n = D и E_n = E. Тогда можно записать

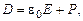
где P = 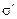, т.е. поляризованность в данном случае равна (по модулю) поверхностной плотности связанных зарядов диэлектрика. Отсюда следует:

Учитывая, что D = e₀e E и E = U/d, найдём

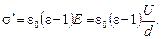
Произведем проверку единиц:

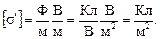
Выполним вычисления по полученной формуле:

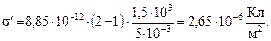
О т в е т: 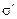= 2,65 мкКл/м².

Пример 9. Диполь с электрическим моментом р = 2 нКл·м находится в однородном электростатическом поле напряженностью Е = 30 кВ/м. Вектор составляет угол α ₀ = 60º с направлением силовых линий поля. Определить произведенную внешними силами работу А для поворота диполя на угол β = 30º.

Д а н о: р = 2 нКл·м, Е = 30 кВ/м, a₀ = 60º, b = 30º А –?

Р е ш е н и е

Из исходного положения (рисунок 5, а) диполь можно повернуть на угол β = 30⁰ = π/6 двумя способами: по часовой стрелке (рисунок 5, б) до угла

α₁ = α₀ – β = π/3 – π/6 = π/6

или против часовой стрелки (рисунок 5, в) до угла

α₂ = α₀ + β = π/3 + π/6 = π/2.

В первом случае диполь будет поворачиваться под действием сил поля. Если кинетическая энергия диполя не меняется (общепринятое предположение), то из теоремы об ее изменении следует, что суммарная работа всех сил, т. е. сил поля и внешних сил, равна нулю. Поэтому работа внешних сил при этом отрицательна и по модулю равна работе сил поля. Во втором случае поворот может быть произведен только под действием внешних сил и, следовательно, работа внешних сил при этом положительна (а работа сил поля – отрицательна).

Работу, совершаемую электрическими силами при повороте диполя, можно вычислить интегрированием выражения элементарной работы, которая при повороте диполя на угол d a определяется по формуле

dA' = Md a = – pE sina d a,

где M – проекция момента электрических сил, действующих на диполь, на ось вращения (при выборе положительного угла a₀ ось направлена на читателя).

Так как проекция момента сил равна:

M = – pE sina,

тогда элементарная работа будет определяться выражением

dA' = – pE sina d a.

а) б) в)

  Рисунок 5

Полная работа при повороте на угол от α₀ до α определяется выражением

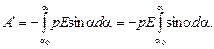
После интегрирования, с учетом вышесказанного, получим

A = – A' = – pE (cosα – cosα₀) = pE (cosα₀ – cosa).

Произведем проверку единиц:

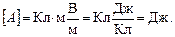
С учетом исходных данных для работы внешних сил при повороте диполя по часовой стрелке будем иметь:

a = π/6;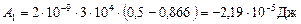

против часовой стрелки:

a = π/2;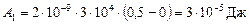

О т в е т: A ₁ = – 21,9 мкДж; A ₂ = 30 мкДж.

Пример 10. К пластинам плоского воздушного (ε₁ = 1,0) конденсатора приложена разность потенциалов U₁ = 1,5 кВ. Площадь пластины S = 150 см², расстояние между ними d = 5 мм. После отключения конденсатора от источника напряжения в пространство между пластинами внесли стекло (ε₂ = 7,0). Определить:

1) разность потенциалов между пластинами после внесения диэлектрика; 2) емкость конденсатора до и после внесения диэлектрика; 3) поверхностную плотность заряда на пластинах до и после внесения диэлектрика.

Д а н о: U ₁=1,5 кВ =1,5·10³ В, S ₁=150 см² = 1,5·10^-2м², ε₁ = 1,0, ε₂ = 7,0, d = 5 мм = 5·10^-3м U _2, C ₁, C ₂, σ₁, σ₂ –?

Р е ш е н и е

Так как конденсатор отключили от источника до замены диэлектрика, то заряд обкладки, а значит, и поверхностная плотность заряда на обкладке остаются постоянными:

s₁ = s₂ = s,

где s – введенное обозначение.

Напряженность электрического поля в плоском конденсаторе может быть определена из двух выражений:

,

поэтому до внесения диэлектрика и после его внесения справедливы соотношения

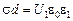и ,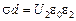

из которых следует:

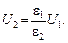
Емкость конденсатора до и после включения диэлектрика определяется соответственно выражениями:

.

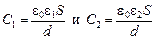Заряд пластин после отключения от источника напряжения не меняется, т. е. Q = const. Поэтому поверхностную плотность заряда на пластинах до и после внесения диэлектрика можно найти по одной из следующих формул:

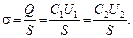
Из четырех конечных формул только последняя нуждается в проверке получающихся единиц:

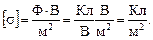
Подставим в полученные соотношения исходные значения и проведем вычисления:

О т в е т: U ₂ = 214 В; C ₁ = 26,5 пФ; C ₂ = 186 пФ; σ = 2,65 мкКл/м².

Пример 11. Определить электрическую емкость плоского конденсатора с двумя слоями диэлектриков: фарфор толщиной 2 мм (ε ₁ = 5,0) и эбонит толщиной 1,5 мм (ε ₂ = 2,7), если площадь каждой пластины равна 100 см².

Д а н о: d ₁ = 2 мм, ε ₁ = 5,0, d ₂ = 1,5 мм, ε ₂ = 2,7, S = 100 см² С –?

Р е ш е н и е

Емкость конденсатора, по определению, С = Q/U, где Q – модуль заряда на одной из пластин конденсатора, U – разность потенциалов между пластинами.

Заменив в этом равенстве общую разность потенциалов суммой U ₁ + U ₂ на слоях диэлектриков, получим

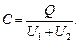(1)

Заряд пластины выразим через его поверхностную плотность (s), а разности потенциалов − через напряженности электрических полей в диэлектриках (E ₁ и E ₂) и электрическое смещение (D) в веществах, которое одинаково, т. к. векторы полей перпендикулярны к поверхностям диэлектриков:

С учетом вышеприведенных формул равенство (1) можно переписать в виде

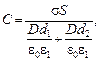(2)

Умножив числитель и знаменатель равенства на ε₀ и учитывая, что D = σ, окончательно получим:

(3)

Проверим размерность полученной формулы:

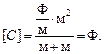
Подставим числовые значения величин в формулу (3):

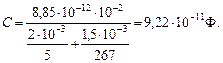
О т в е т: С = 92,2 пФ.

Пример 12. Конденсатор емкостью 3 мкФ заряжен до напряжения 300 В, а конденсатор емкостью 2 мкФ − до 200 В. Определить напряжение между пластинами конденсатора после соединения их: а) одноименно заряженными пластинами; б) разноименно заряженными пластинами. Какое количество теплоты выделится в результате соединения конденсаторов в первом случае?

Д а н о: С₁ = 3 мкФ, U₁ = 300 В, С₂ = 2 мкФ, U₂ = 200 В, S = 100 см² U, U', Q –?

Р е ш е н и е

Конденсаторы соединены параллельно; емкость эквивалентного конденсатора С = С ₁ + С ₂. При соединении одноименно заряженных пластин из закона сохранения заряда следует, что заряд эквивалентного конденсатора

q = q ₁ + q ₂,

где q ₁ и q ₂ - заряды конденсаторов до соединения.

Отсюда и из определения емкости следует:

.

Учитывая по определению емкости, что q ₁ = C ₁ U ₁ и q ₂ = C ₂ U ₂, получим:

.

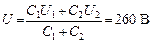Если конденсаторы соединены разноименно заряженными пластинами, то аналогично напряжение между ними:

.

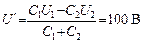Единицы в последних двух формулах очевидны.

Количество выделившейся теплоты определим, пользуясь законом сохранения и превращения энергии. Энергия конденсаторов до и после соединения

; .

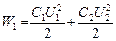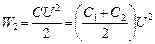Следовательно, искомое количество теплоты

.

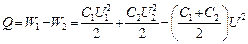Слагаемые в последней формуле по структуре совпадают с известным соотношением для энергии заряженного конденсатора, поэтому проверка единиц не требуется. Вычислим результат:

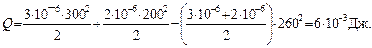
О т в е т: а) U = 260 В; б) U' = 100 В; Q = 6 мДж.

Пример 13. Конденсатор электроемкостью С₁ = 3 мкФ был заряжен до разности потенциалов U₁ = 40 В. После отключения от источника тока конденсатор был соединен параллельно с другим незаряженным конденсатором электроемкостью С₂ = 5 мкФ. Определить энергию ΔW, израсходованную на образование искры в момент присоединения второго конденсатора.

Д а н о: С ₁ = 3 мкФ, U ₁ = 40 В, С ₂ = 5 мкФ Δ W –?

Р е ш е н и е

Энергия, израсходованная на образование искры, определяется по формуле

Δ W = W ₁ – W ₂, (1)

где W ₁ – энергия, которой обладал первый конденсатор до присоединения к нему второго конденсатора; W ₂ – энергия, которую имеет батарея, составленная из первого и второго конденсаторов.

Подставив в выражение (1) формулу для энергии заряженного конденсатора

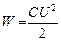
и приняв во внимание, что общая электроемкость параллельно соединенных конденсаторов равна сумме электроемкостей отдельных конденсаторов, получим

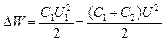, (2)

где U – разность потенциалов на зажимах батареи конденсаторов.

Заряд после присоединения второго конденсатора остался прежним Q = C ₁ U ₁, поэтому из определения электроемкости следует:

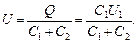(3)

Подставив выражение (3) в формулу (2), получим

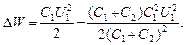
После простых алгебраических преобразований найдем:

По структуре конечная формула совпадает с известным соотношением для энергии конденсатора, поэтому проверка единиц здесь не требуется.

Подставим в эту формулу исходные данные и выполним вычисления:

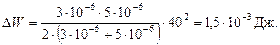
Ответ: Δ W = 1,5 мДж.

Пример 14. Плоский конденсатор заряжен до разности потенциалов U = 1 кВ. Расстояние между пластинами d = 1 см. Диэлектрик – стекло. Определить объемную плотность энергии поля конденсатора.

Д а н о: U = 1 кВ, d = 0,01 м w –?

Решение

Объемная плотность энергии однородного электрического поля

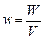, (1)

где W – энергия поля конденсатора (энергия заряженного конденсатора); V – объем, занимаемый полем, т.е. объем пространства, заключенного между пластинами конденсатора.

Энергия заряженного конденсатора определяется по формуле

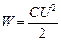, (2)

где U – разность потенциалов, до которой заряжены пластины конденсатора; С – его электроемкость.

Для плоского конденсатора

; ,

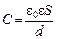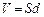где e – диэлектрическая проницаемость (для стекла e = 7); S – площадь пластины конденсатора.

Подставим эти соотношения в (2), а получившуюся формулу − в (1):

(3)

Проверим размерность полученной формулы:

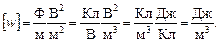
Подставим в формулу (3) исходные данные и выполним вычисления:

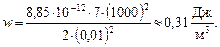
Ответ: w = 0,31 Дж/м³.

Пример 15. Плоский воздушный конденсатор с площадью обкладок S = 200 см² каждая и расстоянием между ними d = 5 мм заряжается до разности потенциалов U₀ = 600 В и отключается от батареи. Как изменяются емкость и энергия конденсатора, если в пространство между обкладками параллельно им внести металлическую пластину такой же площади и толщиной l = 2 мм?

Д а н о: S = 200 см², d ₀ = 5 мм, U ₀ = 600 В, l = 2 мм Δ C, Δ W –?

Решение

Для воздушного плоского конденсатора начальная емкость

.

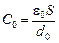Результат внесения незаряженной металлической пластины в пространство между обкладками не зависит от ее конкретного расположения, т. к. она не создает своего электрического поля. Поэтому предположим, что пластина вплотную прижата к одной из обкладок. Это эквивалентно уменьшению расстояния между обкладками до d = d ₀ – l, что вызовет увеличение емкости конденсатора до величины:

.

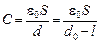Искомое изменение емкости:

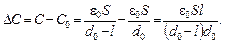
Изменение энергии конденсатора может быть рассчитано двумя способами:

1 Поскольку конденсатор отключен от батареи, заряд на его обкладках остается постоянным и равным Q = C ₀ U ₀. Для расчета энергии конденсатора удобно воспользоваться формулой

.

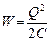Отсюда изменение энергии конденсатора при изменении емкости будет задаваться выражением

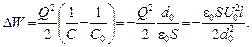(1)

2 Постоянство заряда на обкладках конденсатора обусловливает постоянство напряженности электрического поля между обкладками, следовательно, и плотности энергии этого поля.

В связи с тем, что внутри внесенной металлической пластины поле отсутствует, то убыль энергии конденсатора Δ W равна (с обратным знаком) энергии электрического поля в объеме металлической пластинки (если бы оно там было):

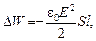
где Е – модуль напряженности поля между обкладками.

Для однородного электрического поля Е = U ₀/ d ₀, (удобно выразить напряженность через начальные параметры). С учетом этого получим окончательное выражение

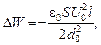
что совпадает с формулой (1).

Проверим единицы в конечных формулах:

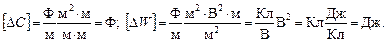
Подставим в них численные значения и получим:

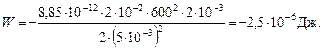
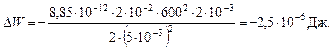
Ответ: Δ C = 23,6 пФ; Δ W= –2,5 мкДж.

Пример 16. Определить плотность электрического тока в медном проводнике (удельное сопротивление r = 17 нОм×м), если удельная тепловая мощность тока w = 1,7 Дж/(м ³× с).

Д а н о: p_V = 1,7 Дж/(м³×с), r = 17 нОм×м j –?

Р е ш е н и е

Согласно законам Джоуля-Ленца и Ома в дифференциальной форме

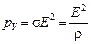, (1)

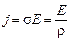, (2)

где s - удельная проводимость материала проводника; E – напряженность электрического поля в металле.

Из (2) получим, что E = r j. Подставив это выражение в (1), найдем искомую плотность тока:

.

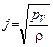Проверим единицы в конечной формуле:

Подставим в нее численные значения и получим:

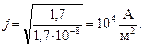
О т в е т: j = 10⁴ А/м².

Пример 17. Сила тока в проводнике равномерно растет от 1 до 3 А за время 6 с. Сопротивление проводника 50 Ом. Определить выделившееся за это время количество теплоты.

Д а н о: I ₀ = 1 А, I _max = 3 А, t = 6 с, R = 50 Ом Q –?

Р е ш е н и е

Согласно закону Джоуля-Ленца за бесконечно малый промежуток времени dt выделится теплота

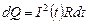. (1)

По условию задачи сила тока в проводнике равномерно растет, что можно описать с помощью уравнения

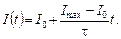(2)

Проинтегрируем выражение (1):

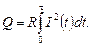(3)

Сделаем замену переменных в интеграле 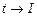. Из (2) следует:

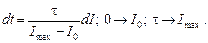
В новых переменных соотношение принимает вид

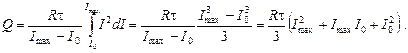
Конечная формула по структуре совпадает с известным выражением для закона Джоуля − Ленца, поэтому проверка единиц не требуется.

Подставим в нее численные значения и получим:

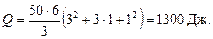
О т в е т: Q = 1300 Дж.

Пример 18. Источник тока с ЭДС 12 В замкнут медным проводом длиной 5 м и диаметром поперечного сечения 0,2 мм. Сила тока в цепи равна 2 А. Найти внутреннее сопротивление источника и падение напряжения во внешней части цепи.

Д а н о: e = 12 В, l = 5 м, d = 0,2×10^–3 м, I = 2 A r, U –?

Р е ш е н и е

Воспользуемся законом Ома для замкнутой цепи

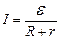, (1)

где R – сопротивление нагрузки (в данном случае – медного провода);

,

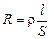где r – удельное сопротивление материала проволоки (в данном случае – меди); 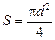– площадь сечения проволоки. Отсюда

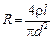. (2)

Из формулы (1) получим:

.

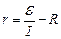Подставим сюда соотношение (2):

.

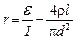Проверим единицы измерения:

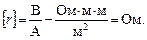
Подставив в формулу значения величин и произведя вычисления, получим:

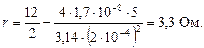
Падение напряжения на внешней части цепи определим по закону Ома для однородного участка цепи и формуле (2):

.

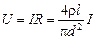Проверим единицы измерения:

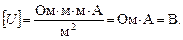
Подставив в формулу значения величин и произведя вычисления, получим:

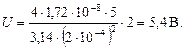
О т в е т: r = 3,3 Ом, U = 5,4 В.

Пример 19. Б атарея из двух элементов с ЭДС e ₁ = 8 В и e ₂ = 4 В, внутренние сопротивления которых r ₁ = 1 Ом, r ₂ = 0,5 Ом, подключена к резистору с сопротивлением R = 50 Ом по схеме, показанной на рисунке 6. Определить силу тока через резистор.

Д а н о: e ₁ = 8 В, e ₂ = 4В, r ₁ = 1 Ом, r ₂ = 0,5 Ом, R= 50 Ом I –?

Р е ш е н и е

Выберем направление обхода контуров по часовой стрелке и применим правила Кирхгофа для каждого из контуров.

По первому правилу Кирхгофа для узла А:

I ₂ + I = I ₁. (1)

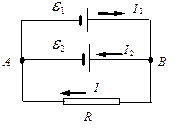
а)	б)
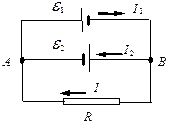
Рисунок 6

Если источники соединены так, как показано на рисунке 6, а, то для контуров e ₁ ВRAe ₁ и e ₂ ВRAe ₂ по 2-му правилу Кирхгофа

I ₁ r ₁ + IR = e ₁ и - I ₂ r ₂ + IR = e ₂. (2)

Выразив из (2) значения для I ₁ и I ₂ и подставив в (1), получим:

,

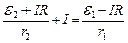откуда .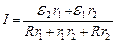

Подставив в формулы значения величин и произведя вычисления, получим:

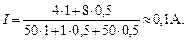
Если источники соединены так, как изображено на рисунке 6, б, то согласно 2-му правилу Кирхгофа для контуров будем иметь:

а) контура e ₁ ВRAe ₁ I ₁ r ₁ + IR = - e ₁,

б) контура e ₂ ВRAe ₂ - I ₂ r ₂ + IR = e ₂.

Совместное решение уравнений дает

.

О т в е т: а) I = 0,1 А; б) I = 0.

Пример 20. Электрическая лампа горит под напряжением 50 В и потребляет мощность 500 Вт. Определить, на сколько градусов нагреются подводящие провода через 1 мин после включения лампы, если проводка выполнена медным проводом сечением 1 мм² и половина выделившейся теплоты отдана окружающим телам; число электронов, проходящих через поперечное сечение провода за 1 с; среднюю скорость упорядоченного движения электронов, считая число электронов в проводнике равным числу атомов.

Д а н о: U = 50 В, P = 500Вт, t = 1 мин, S = 1 мм², h = 0,5 D t, n, v –?

Р е ш е н и е

Дата добавления: 2014-12-16