Расчет емкости и энергии заряженного конденсатора 2 страница

Количество теплоты, выделившееся в проводах за время t, определим по закону Джоуля − Ленца

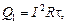
где I – сила тока через лампу, R – сопротивление проводов.

Количество теплоты, пошедшей на нагревание проводника,

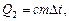
где с – удельная теплоемкость; m = r Sl - масса проводника; r - плотность меди; l – длина проводов.

По условию Q ₂ = h Q ₁, отсюда

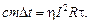(1)

Используем формулы для мощности тока и сопротивления цилиндрического проводника

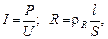
где r _R – удельное сопротивление меди. Из этих соотношений и формулы (1) получим:

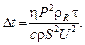(2)

Число электронов, проходящих через поперечное сечение за 1 с, получим исходя из определения силы тока:

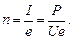(3)

Среднюю скорость упорядоченного движения электронов найдем из выражения для плотности тока

;

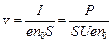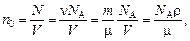
где n ₀ - число атомов (свободных электронов) в единице объема;
N – число атомов в объеме V; n – количество вещества; N _A – число Авогадро; m и m – масса и молярная масса вещества.

Следовательно,

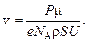(4)

Проверим единицы в соотношениях (2) – (4):

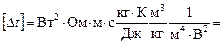
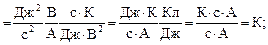
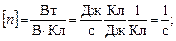
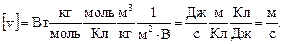
Подставив в формулы значения величин и произведя вычисления, получим:

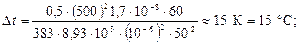
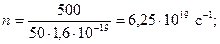
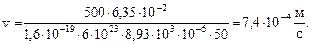
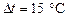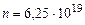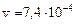О т в е т: , с^-1, м/с.

Пример 21 Какой длины надо взять нихромовый проводник, имеющий сечение 0,1 мм², чтобы изготовить нагреватель, на котором можно за время 5 мин довести до кипения 1,5 л воды, взятой при температуре 20 °С? Напряжение в сети 220 В. КПД кипятильника 90 %.

Д а н о: S = 0,1 мм², t= 5 мин, V = 1,5 л, U = 220 B, η = 90 %, ρ _R = 1,1 мкОм×м, t ₁ = 20 ºC, t ₂ = 100 ºC, r = 1 кг/м³ l –?

Р е ш е н и е

Масса воды т = r V. Для нагревания ей требуется сообщить количество теплоты

,

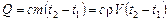где с – удельная теплоемкость.

Расход энергии нагревателя по закону Джоуля − Ленца

,

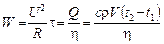где 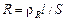– сопротивление проволоки, из которой изготовлен нагреватель. Подставляя, получим

.

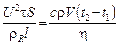Отсюда искомая длина проводника

.

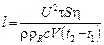Проверим единицы в конечной формуле:

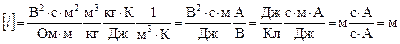
Подставим в формулу значения величин

.

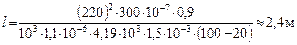О т в ет: l = 2,4 м.

Пример 22. Пространство между пластинами плоского конденсатора имеет объем V = 375 см³ и заполнено частично ионизированным газом. Площадь пластины конденсатора S = 250 см ². При каком напряжении U между пластинами конденсатора сила тока, протекающего через конденсатор, достигнет значения I = 2 мкА, если концентрация пар ионов в газе равна 5,3×10⁷ см ^-3? Принять подвижность ионов u₊ = 5,4×10 ^{- 4} м²/(В×с), u_- = 7,4×10^-4 м ²/(В×с).

Д а н о: V = 375 см³, S = 250 см², I = 2 мкА, n =5,3×10⁷ см^-3, u₊ = 5,4×10^-4 м²/(В×с), u_- = 7,4×10^-4 м ²/(В×с) U –?

Р е ш е н и е

Напряжение на пластинах конденсатора связано с напряженностью однородного электрического поля между пластинами E и расстоянием между ними d соотношением

U = Ed. (1)

Напряженность поля может быть найдена из выражения для плотности тока (закон Ома для газов):

,

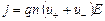где q = e - заряд одного иона по модулю. Отсюда

.

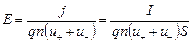Расстояние между пластинами, входящее в формулу (1), найдем из геометрического соотношения для объема d = V / S.

Подставив выражения Е и d в (1), получим

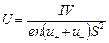. (2)

Проверим единицы в формуле (2)

.

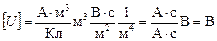Подставим в формулу (2) значения величин:

.

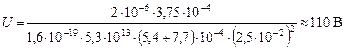О т в е т: U = 110 B.

ЗАДАНИЯ К КОНТРОЛЬНОЙ РАБОТЕ № 3

3.1 Два малых одинаковых металлических шарика имеют заряды
q ₁ = 5,6 мкКл и q ₂ = –7,2 мкКл. Найти силу их кулоновского взаимодействия после того, как их привели в соприкосновение, а затем удалили друг от друга на расстояние l = 14 см. Диаметры шариков существенно меньше расстояния между ними.

3.2 Два маленьких проводящих шарика подвешены на длинных непроводящих нитях к одной точке. Шарики заряжены одинаковыми зарядами и находятся на расстоянии 5 см друг от друга. Как изменится расстояние между шариками после того, как один из шариков разрядили?

3.3 Два одинаковых металлических шарика имеют заряды
q ₁ = 3,6 нКл и q ₂ = 8 нКл. Найти силу их взаимодействия после соприкосновения и удаления друг от друга на расстояние l = 12 см.

3.4 В вершинах равностороннего треугольника со стороной 2 см находятся одинаковые положительные заряды по 0,46 мкКл каждый. Найти силу, действующую на каждый из этих зарядов.

3.5 Тонкий стержень длиной 15 см равномерно заряжен. Линейная плотность заряда 6 мкКл/м. Заряд 12 нКл равноудален от концов стержня на расстояние 10 см. Найти силу взаимодействия стержня и точечного заряда.

3.6 Расстояние между двумя точечными зарядами q ₁ = 1 мкКл и
q ₂= – 1 мкКл равно 10 см. Найти силу, действующую на точечный заряд q ₀ = 0,1 мкКл, удаленный на 6 см от первого и на 8 см от второго зарядов.

3.7 Тонкий стержень длиной 10 см несет равномерно распределенный заряд с линейной плотностью τ = 1 мкКл/м. На продолжении оси стержня на расстоянии 20 см от ближайшего конца находится точечный заряд 100 нКл. Найти силу взаимодействия заряженного стержня и точечного заряда.

3.8 Тонкая нить длиной l = 20 см заряжена с линейной плотностью t= 10 нКл/м. На расстоянии l ₁ = 10 см от нити, против ее середины, находится точечный заряд q ₀= 1 нКл. Вычислить силу, действующую на этот заряд со стороны заряженной нити.

3.9 На двух одинаковых маленьких капельках воды находится по одному лишнему электрону. Определить радиус капелек, если сила электростатического отталкивания уравновешивает силу их гравитационного притяжения.

3.10 Два одинаковых заряженных шарика, подвешенных на нитях одинаковой длины, опускаются в глицерин. Какой должна быть плотность материала шариков, чтобы угол расхождения нитей не изменился?

3.11 Два заряженных шарика массой по 10 г подвешены на нитях длиной 1 м каждая к одной точке, в которой находится третий шарик с таким же зарядом. Определить заряды шариков и силу натяжения нитей, если угол расхождения их в положении равновесия равен 60º.

3.12 Шарик массой 10 г и зарядом 2 мкКл, подвешенный на нити длиной 1 м, вращается в горизонтальной плоскости вокруг такого же неподвижного шарика. Определить угловую скорость равномерного вращения и силу натяжения нити, если нить образует с вертикалью угол 60º.

3.13 Сила электростатического отталкивания уравновешивает силу гравитационного притяжения двух одинаковых капелек воды радиусом 0,1 мм. Определить заряд капель.

3.14 Два заряженных шарика, подвешенных на нитях одинаковой длины, опускаются в керосин. Какой должна быть плотность материала шариков, чтобы угол расхождения нитей в воздухе и в керосине не изменился?

3.15 Два шарика массой 5 г каждый подвешены на нитях длиной 5 м так, что они соприкасаются друг с другом. Шарикам сообщают одноименные заряды 80 нКл. На какое расстояние они разойдутся после зарядки?

3.16 На тонкой прямой металлической проволоке длиной 8 см равномерно распределен заряд q ₀ = 350 мкКл, действующий с силой 120 мкН на точечный заряд q, который находится на продолжении той же проволоки на расстоянии 6 см от ее середины. Определить величину точечного заряда q.

3.17 Два одинаковых шарика массой 20 мг каждый подвешены на нитях длиной 0,2 м, закрепленных в одной точке подвеса. Один из шариков отвели в сторону и зарядили. После соприкосновения с другим шариком они разошлись так, что нити образовали угол 60º. Определить величину заряда, сообщенного первому шарику.

3.18 Два одинаковых шарика подвешены на нитях одинаковой длины. При сообщении им заряда они разошлись на угол 80º.^. Через некоторое время шарики сблизились до угла 60º. Какая доля первоначального заряда осталась на каждом из шариков?

3.19 Два одноименных заряда 0,7 и 1,3 нКл находятся на расстоянии 6 см друг от друга. На каком расстоянии между ними нужно поместить третий заряд, чтобы результирующая сила, действующая на каждый заряд, была равна нулю?

3.20 Два точечных заряда величиной 1,1 нКл каждый находятся на расстоянии 17 см. С какой силой они действуют на такой же заряд, находящийся на расстоянии 17 см от каждого из них?

3.21 В сосуд с маслом погружен эбонитовый шарик радиусом 0,01 м и зарядом 20 мКл. Определить, при какой напряженности вертикального электростатического поля шарик будет находиться во взвешенном состоянии.

3.22 Расстояние между зарядами q ₁ = – 1 нКл и q ₂ = 10 нКл равно l = 0,55 м. Определить напряженность поля E в точке на прямой, проходящей через заряды, в которой потенциал φ равен нулю.

3.23 В двух противоположных вершинах квадрата со стороной 0,1 м находятся заряды величиной 0,2 мкКл каждый. Определить напряженность и потенциал электростатического поля в двух других вершинах квадрата.

3.24 Сплошная металлическая сфера радиусом 20 см равномерно заряжена с поверхностной плотностью заряда, равной 1 нКл/м²_. Определить напряженность и потенциал электростатического поля в точках: а) на расстоянии 16 см от центра сферы; б) на внешней поверхности сферы; с) на расстоянии 36 см от центра сферы. Построить графики Е = Е(r) и j = j (r).

3.25 Точечные заряды q ₁= 20 нКл и q ₂ = – 10 нКл находятся на расстоянии d = 10 см друг от друга. Определить напряженность поля в точке, удаленной на расстояние r ₁ = 8 см от первого и r ₂ = 7 см от второго зарядов.

3.26 В вершинах квадрата со стороной 5 см находятся одинаковые заряды 2 нКл. Определить напряженность и потенциал электростатического поля в центре квадрата.

3.27 Точечные заряды q ₁ = – 2 нКл и q ₂ = 4 нКл находятся на расстоянии d ₁ = 60 см друг от друга. Определить напряженность поля в точке, лежащей посередине между зарядами. Чему будет равна напряженность, если первый заряд положительный?

3.28 В вершинах квадрата со стороной 5 см находятся одинаковые заряды 2 нКл. Определить напряженность и потенциал электростатического поля в середине одной из сторон квадрата.

3.29 Поле создано двумя равномерно заряженными концентрическими сферами радиусами R ₁ = 5 см и R ₂ = 8 см. Заряды сфер равны q ₁ = 2 нКл и q ₂ = – 1 нКл соответственно. Определить напряженность электростатического поля в точках, лежащих от центра сфер на расстояниях: 1) r ₁ = 3 cм; 2) r ₂ = 6 см; 3) r ₃= 10 см. Построить график зависимости Е(r).

3.30 Шар радиусом 10 см равномерно заряжен с объемной плотностью 10 нКл/м³. Определить напряженность электростатического поля на расстояниях r ₁ = 5 cм и r ₂ = 15 cм от центра шара. Построить график зависимости Е(r).

3.31 Капля массой m = 5,6×10^-9 г поднимается вертикально вверх между пластинами горизонтально расположенного конденсатора с ускорением a = 1,2 м/с². Найти поверхностную плотность заряда s на пластинах конденсатора, если заряд капли равен 10 зарядам электрона.

3.32 Найти силу F, действующую на заряд q = 8,3 нКл, находящийся на расстоянии r = 5,2 см от бесконечно длинной нити, заряженной равномерно с линейной плотностью заряда t = 30 мкКл/м.

3.33 Бесконечная плоскость несет заряд, равномерно распределенный с поверхностной плотностью s = 1 мкКл/м². На некотором расстоянии от плоскости параллельно ей расположен круг радиусом r = 10 см. Вычислить поток вектора напряженности Ф _Е через этот круг.

3.34 Плоская квадратная рамка со стороной длиной a = 10 см находится на некотором расстоянии от бесконечной равномерно заряженной плоскости. Плоскость пластины с линиями поля составляет угол j = 30º. Поверхностная плотность заряда s = 1 мкКл/м². Вычислить поток вектора напряженности Ф _Е через эту пластину.

3.35 Бесконечная плоскость несет заряд, равномерно распределенный с поверхностной плотностью s = 20 нКл/м². Параллельно ей расположена прямая тонкая нить, заряженная равномерно с линейной плотностью заряда t = 0,4 нКл/м. Определить силу, действующую на отрезок нити длиной 1 м.

3.36 Протон, летящий по направлению к неподвижному ядру гелия, в некоторой точке напряженностью 10⁴ В/м имеет скорость
1 Мм/с. На какое расстояние протон сможет приблизиться к ядру?

3.37 Кольцо радиусом 5 см из тонкой проволоки равномерно заряжено с линейной плотностью 14 нКл/м. Определить напряженность электростатического поля на оси, проходящей через центр кольца, в точке, удаленной на расстояние 10 см от центра кольца.

3.38 Заряд 20 нКл равномерно распределен на металлической прямой нити длиной 1 м. Определить напряженность поля в точке, находящейся на расстоянии 10 см от нити и равноудаленной от ее концов.

3.39 Два неподвижных одноименных заряда q = 1,6×10^-19 Кл каждый находятся на расстоянии r = 3,9×10^-11 м. Вдоль перпендикуляра, проходящего через середину отрезка, соединяющего эти заряды, движется электрон. Найти максимальную силу взаимодействия F _max электрона и этих зарядов.

3.40 В однородном электростатическом поле равномерно вращается шарик массой 0,5 г с положительным зарядом 10 нКл, подвешенный на нити длиной 0,5 м. Определить силу натяжения нити и кинетическую энергию шарика, если напряженность поля направлена вертикально вниз и равна 100 кВ/м. Нить образует с вертикалью угол 60º.

3.41 Вблизи бесконечной заряженной плоскости находится точечный заряд 10^-8 Кл. Под действием поля заряд перемещается вдоль силовой линии на расстояние 17,7 см. При этом совершается работа
1 мДж. Определить поверхностную плотность заряда.

3.42 Кольцо радиусом 5 см из тонкой проволоки несет равномерно распределенный заряд 10 нКл. Определить потенциал электростатического поля на оси, проходящей через центр кольца, в точке, удаленной на расстояние 10 см от центра кольца.

3.43 Сфера радиусом 5 см равномерно заряжена с поверхностной плотностью 1 нКл/м²_. Определить разность потенциалов электростатического поля между точками этого поля, лежащими на расстояниях
10 см и 15 см от центра сферы.

3.44 Найти силу отталкивания (на единицу длины) двух одноименно заряженных бесконечно длинных параллельных нитей с одинаковой линейной плотностью заряда 3 мкКл/м, находящихся в вакууме на расстоянии 2 см друг от друга. Найти также работу (на единицу длины), которую нужно совершить, чтобы сблизить эти нити до расстояния 1 см.

3.45 Положительные заряды q ₁ = 3,7 × 10^-5 Кл и q ₂ = 6,2 × 10^-5 Кл находятся в вакууме на расстоянии r ₁ = 2,7 м друг от друга. Найти работу, которую нужно совершить, чтобы сблизить заряды до расстояния r ₂ = 45 см.

3.46 Найти работу, которую нужно совершить, чтобы перенести точечный заряд q = 42 нКл из точки, отстоящей на расстоянии 1 м, в точку, находящуюся на расстоянии 1,5 см от поверхности шара радиусом R = 2,3 см, заряженного с поверхностной плотностью заряда s = 4,3 × 10^-11 Кл/м².

3.47 Бесконечно длинная нить заряжена равномерно с линейной плотностью заряда t = 63 мкКл/м. Найти работу сил поля по перемещению точечного q = 2,1 нКл с расстояния a = 2,4 см до расстояния
b = 4,8 см от нити.

3.48 Две удаленные от остальных тел одинаковые металлические пластины площадью S = 50 см² каждая находятся на расстоянии
d = 1 мм друг от друга и заряжены: одна зарядом q ₁ = 20 мкКл, вторая q ₂ = – 40 мкКл. Найти разность потенциалов Dj между ними.

3.49 Две концентрические проводящие сферы заряжены одноименно. Их радиусы равны 12 и 18 см. Заряд внутренней сферы равен 1 мкКл, а внешней – 2 мкКл. Найти разность потенциалов Djмежду сферами.

3.50 Две бесконечные параллельные плоскости отстоят на расстоянии d = 1 см друг от друга. Плоскости равномерно заряжены, поверхностные плотности заряда соответственно s₁ = 0,2 мкКл/м² и s₂ = 0,5 мкКл/м². Найти разность потенциалов между пластинами.

3.51 Электрическое поле создано положительным точечным зарядом. Потенциал поля в точке, удаленной от заряда на r = 12 см, равен 24 В. Определить значение и направление градиента потенциала поля в этой точке.

3.52 Электростатическое поле создается положительно заряженной бесконечной нитью,заряженной равномерно с линейной плотностью τ = 100 пКл/см. Определить значение и направление градиента потенциала поля в точке, удаленной от нити на r = 12 см.

3.53 Электростатическое поле создается бесконечной плоскостью, равномерно заряженной с поверхностной плотностью
s = 5 нКл/м². Определить разность потенциалов между двумя точками, лежащими на расстояниях r ₁ = 20 см и r ₂ = 40 см от плоскости.

3.54 Электростатическое поле создается равномерно заряженной сферической поверхностью радиусом R = 15 см с общим зарядом
Q = 30 нКл. Определите разность потенциалов между двумя точками этого поля, лежащими на расстояниях r ₁= 10 см и r ₂ = 20 см от поверхности сферы.

3.55 Электростатическое поле создается шаром радиусом
R = 10 см, равномерно заряженным с объемной плотностью
ρ = 10 нКл/м³. Определите разность потенциалов между двумя точками этого поля, лежащими на расстояниях r ₁ = 15 см и r ₂= 25 см от центра шара.

3.56 Бесконечная плоскость несет заряд, равномерно распределенный с поверхностной плотностью s= 4 нКл/м². Определить значение и направление градиента потенциала поля, созданного этой плоскостью.

3.57 Электрон влетел в пространство между пластинами плоского конденсатора параллельно пластинам с начальной скоростью
v ₀= 10 Мм/с. Насколько приблизится электрон к положительной пластине за время движения внутри конденсатора, если разность потенциалов U = 30 В, расстояние d между пластинами равно 16 мм и длина пластин l = 6 см?

3.58 Электрон влетел в пространство между пластинами плоского конденсатора параллельно пластинам с начальной скоростью
v ₀ = 10 Мм/с. При вылете из конденсатора направление скорости электрона составляло угол a = 35º с первоначальным направлением скорости. Определить разность потенциалов между пластинами, если длина пластин равна 10 см, а расстояние между ними 2 см.

3.59 В вершинах треугольника со сторонами АВ = 0,3 м,
ВС= 0,5 м и АС = 0,6 м находятся три точечных заряда q_А = 3 мкКл, q_В = 5 мкКл, q_С = – 6 мкКл. Какую работу нужно совершить, чтобы развести эти заряды на расстояние, чтобы силы их взаимодействия можно было считать равными нулю?

3.60 Определить потенциал j, до которого можно зарядить уединенный металлический шар радиусом R = 10 см, если напряженность поля, при которой происходит пробой воздуха, Е = 3 МВ/м. Найти также максимальную поверхностную плотность s электрических зарядов перед пробоем.

3.61 Металлический шарик диаметром d = 2 см заряжен отрицательно до потенциала j = –150 В. Сколько избыточных электронов N находится на поверхности шарика?

3.62 В вершинах квадрата со стороной 10 см находятся одинаковые заряды 100 нКл. Определить потенциальную энергию этой
системы.

3.63 Кольцо радиусом 5 см из тонкой проволоки несет равномерно распределенный заряд 10 нКл. Определить потенциал электростатического поля в центре кольца.

3.64 Два шара диаметром d ₁ = 1 см и d ₂ = 3 см и зарядами q ₁ = 5 нКл и q ₂ =15 нКл соединяют проводником. Определить величину переместившегося заряда.

3.65 В вершинах равностороннего треугольника со стороной
10 см находятся одинаковые заряды 100 нКл. Определить потенциальную энергию этой системы.

3.66 Шар диаметром d ₁ =1 см, заряженный до потенциала 500 В, соединяется проводником с незаряженным шаром. После соединения потенциал шаров стал равным 200 В. Найти диаметр второго шара.

3.67 Электростатическое поле создается в вакууме бесконечным цилиндром радиусом 10 см, равномерно заряженным с линейной плотностью τ = 10 нКл/м. Определить разность потенциалов между двумя точками этого поля, лежащими на расстояниях r ₁= 2 мм и
r ₂= 7 мм от поверхности этого цилиндра.

3.68 По тонкому кольцу радиуса R = 5 см равномерно распределен заряд с линейной плотностью τ = 20 нКл/м. Определить потенциал в точке, лежащей на оси кольца на расстоянии r = 5 см от плоскости кольца.

3.69 Определить потенциал в центре тонкого кольца радиуса
R = 15 см, по которому равномерно распределен заряд с линейной плотностью τ = 10 нКл/м.

3.70 Шар диаметром d =10 см заряжается отрицательно до потенциала φ = 1 кВ. Найти общую массу избыточных электронов.

3.71 Десять заряженных водяных капель радиусом 1 мм и зарядом 0,3 нКл каждая сливаются в одну большую каплю. Определить потенциал большой капли.

3.72 Найти соотношение между радиусом шара R и максимальным потенциалом φ, до которого он может быть заряжен в воздухе, если считать, что разряд в воздухе происходит при напряженности поля Е = 3 МВ/м.

3.73 Точечные заряды q ₁ = 2 нКл и q ₂ =10 нКл находятся на расстоянии r ₁ = 5 см друг от друга. Найти работу сил поля, если второй заряд удалится на расстояние: 1) r ₂ = 10 см, 2) r ₃ = ∞.

3.74 Электростатическое поле создается бесконечной плоскостью, равномерно заряженной с поверхностной плотностью
s = 50 нКл/м². Определить разность потенциалов между двумя точками этого поля, лежащими на расстояниях r ₁ = 10 см и r ₂ = 200 см от плоскости.

3.75 Электростатическое поле создается равномерно заряженной сферической поверхностью радиусом R = 10 см с общим зарядом
Q = 10 нКл. Определите разность потенциалов между двумя точками этого поля, лежащими на расстояниях r ₁ = 10 см и r ₂ = 20 см от поверхности сферы.

3.76 Эбонитовый толстостенный полый шар несет равномерно распределенный по объему заряд q =20 мкКл/м³. Внутренний радиус шара R ₁ = 2см, наружный R ₂ = 4 см. Определить потенциал шара в следующих точках: 1) на наружной поверхности шара; 2) на внутренней поверхности шара; 3) в центре шара.

3.77 Две бесконечные плоскости, равномерно заряженные с поверхностной плотностью σ = 0,5 мкКл/м², пересекаются под углом
α = 60º. Начертить картину эквипотенциальных поверхностей и вычислить работу сил поля по перемещению заряда q = 1 нКл из точки А, лежащей в одной из плоскостей на расстоянии l ₁ от линии пересечения плоскостей, в точку В,лежащую в другой плоскости на расстоянии l ₂ от той же линии.

3.78 На отрезке прямого провода равномерно распределен заряд с линейной плотностью τ = 1 мкКл/м. Определить работу А сил поля по перемещению заряда q = 1нКл из точки В, лежащей на продолжении оси провода на расстоянии l ₁ от конца провода, в точку С, лежащую на продолжении той же оси на расстоянии 2 l ₁ от конца
провода.

3.79 Тонкий стержень согнут в полукольцо. Стержень заряжен с линейной плотностью заряда τ = 100нКл/м. Какую работу надо совершить, чтобы перенести заряд q = 5 нКл из центра полукольца в бесконечность?

3.80Тонкий стержень согнут в кольцо радиуса R = 15 см. Он заряжен с линейной плотностью заряда τ = 500 нКл/м. Какую работу надо совершить, чтобы перенести заряд q = 10нКл из центра кольца в точку А, расположенную на оси кольца на расстоянии l =20 см от его центра?

3.81 В однородное электростатическое поле напряженностью
Е ₀ = 700 В/м перпендикулярно полю помещается бесконечная плоскопараллельная стеклянная пластинка. Определить поверхностную плотность связанных зарядов σ ' на стекле.

3.82 Пространство между пластинами плоского конденсатора заполнено парафином. Расстояние между пластинами равно 8,85 мм. Какую разность потенциалов нужно подать на пластины, чтобы поверхностная плотность связанных зарядов на парафине составляла
σ ' = 0,1 нКл/см²?

3.83 Расстояние между пластинами плоского конденсатора
d = 5 мм. После зарядки конденсатора до разности потенциалов
∆φ = 500 В между пластинами конденсатора вдвинули стеклянную пластинку. Определить поверхностную плотность связанных зарядов σ ' на стеклянной пластинке.

3.84 Определить поверхностную плотность связанных зарядов σ ' на слюдяной пластинке толщиной d =1 мм, служащей изолятором плоского конденсатора, если разность потенциалов между пластинами конденсатора ∆φ = 300 В.

3.85 Между пластинами плоского конденсатора помещено два слоя диэлектрика: слюдяная пластинка толщиной d ₁ = 1 мм и парафин толщиной d ₂ = 0,5 мм. Разность потенциалов между пластинами конденсатора U = 500 В. Определить: 1) напряженность электростатических полей в слоях диэлектрика; 2) электрическое смещение.

Дата добавления: 2014-12-16