Формула для расчета параллельного соединения сопротивлений

Графическое обозначение схемы параллельного соеднинения

Определение параллельного соединения

Параллельное соединение электрических элементов (проводников, сопротивлений, емкостей, индуктивностей) - это такое соединение, при котором подключенные элементы цепи имеют два общих узла подключения.

Другое определение: сопротивления подключены параллельно, если они подключены одно и той же паре узлов.

На приведенном рисунке показана схема параллельное подключения сопротивлений R1, R2, R3, R4. Из схемы видно, что все эти четыре сопротивления имеют две общие точки (узла подключения).

В электротехнике принято, но не строго требуется, рисовать провода горизонтально и вертикально. Поэтому эту же схему можно изобразить, как на рисунке ниже. Это тоже параллельное соединение тех же самых сопротивлений.

При параллельном соединении обратная величина от эквивалентного сопротивления равна сумме обратных величин всех параллельно подключенных сопротивлений. Эквивалентная проводимость равна сумме всех параллельно подключенных проводимостей электрической схемы.

Для приведенной выше схемы эквивалентное сопротивление можно рассчитать по формуле:

В частном случае при подключении параллельно двух сопротивлений:

Эквивалентное сопротивление цепи определяется по формуле:

В случае подключения "n" одинаковых сопротивлений, эквивалентное сопротивление можно рассчитать по частной формуле:

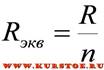
Смешанное соединение. Это сочетание последовательного и параллельного соединения элементов.

Эквивалентное сопротивление для последовательно-параллельного соединения элементов:

R_экв= R₁+R₂R₃/ (R₂+R₃)

Сложное соединение. Это соединение, имеющее три и более узлов. В сложных цепях встречаются соединения сопротивлений в виде звезды и треугольника.

Формулы преобразования треугольника сопротивлений в эквивалентную трехлучевую звезду имеют вид:

,

,

Формулы обратного преобразования ветвей трехлучевой звезды в эквивалентный треугольник:

,

_{РЕЖИМЫ РАБОТЫ ИСТОЧНИКОВ ПИТАНИЯ}

Различают четыре режима работы источников питания. Е

Режим холостого хода. В режиме холостого хода концы источника разомкнуты: (R_х= ∞).

Этот режим используют для измерения ЭДС источника. Параметры режима холостого хода: I_х= 0; R_х= ∞; U_х= E; (U_х=E-Ir; r= 0; U_х= E)

Режим короткого замыкания. В режиме короткого замыкания концы источника соединены накоротко: (R_к= 0).

Ro E

Номинальный режим. Это режим работы источника питания при номинальных значениях тока и напряжения. Номинальные значения тока и напряжения приводятся в паспорте источника питания.

Согласованный режим. Это режим работы источника питания с максимальной мощностью Р=Р_mах.Такое возможно при условии, когда R_вн =R_вш. Формула мощности для согласованного режима:

P_max= I²R = E² / 4R.

E R

Дата добавления: 2014-12-16