Пример решения на ПЭВМ. Программное обеспечение

Программное обеспечение

Для решения начально-краевой задачи для параболического уравнения в Matlab’е используется описанная ранее среда PDE Tool. Процесс построения решения начально-краевой задачи для параболического уравнения с её помощью показан ниже на примере решения конкретной задачи.

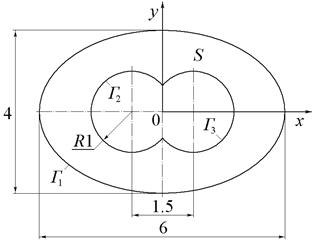Условия задачи. Найти решение начально-краевой задачи для параболического уравнения

,

,

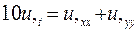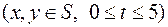где область S поиска решения показана на рис.2. На границе Г области S заданы следующие граничные условия

,

,

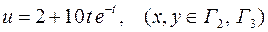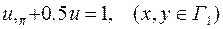а начальное условие имеет вид

.

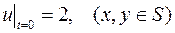Решение. Процесс построения решения начально-краевой задачи для параболического уравнения в среде PDE Tool аналогичен описанному ранее для краевой задачи с эллиптическим уравнением.

Сначала надо задать систему глобальных координат и нарисовать область S поиска решения, как это показано на рис.3.

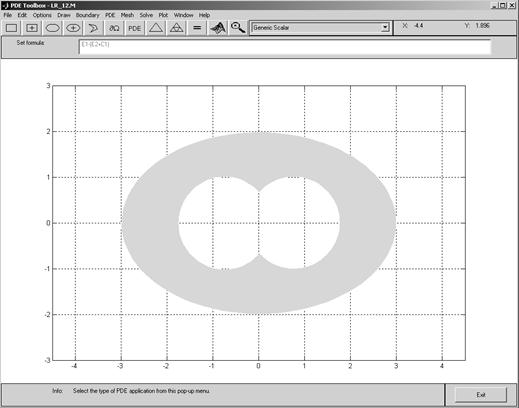
Рис.3.

Рисование области S, осуществляемое с помощью мыши, характеризуется существенными погрешностями. Однако их можно избежать. Для этого достаточно сделать двойной щелчок по нарисованному объекту. Это выведет на экран окно его свойств (см. рис.4). Так для эллипса можно точно задать координаты его центра (X-center, Y-center) и радиусы полуосей (A-semiaxes, B-semiaxes).

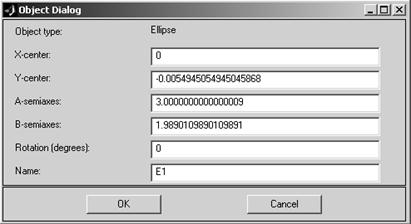
Рис.4.

После этого надо привести параболическое уравнение и его граничные условия к используемому в среде PDE Tool виду

,

,

и задать в пункте меню PDE Specification тип уравнения – parabolic и коэффициенты c=1, a=0, f=0, d=10, а в пункте Specify Boundary Conditions – условия для границы Г ₁ – тип Neumann, g=1, q=0.5 и условия для границ Г ₂, Г ₃ – тип Dirichlet, h=1, r=2+10*t.*exp(-t).

Следующим шагом является формирование конечно-элементной сетки в области поиска решения c помощью меню Mesh. После подбора степени густоты сетки в рабочем окне получается изображение, показанное на рис.5.

Последним шагом в этой процедуре является построение конечно-элементного решения с помощью пункта меню Solve, но с одним отличием. Оно заключается в том, что до решения задачи Коши, к которой сводится начально-краевая задача для параболического уравнения, необходимо установить диапазон изменения времени t и задать

Рис.5.

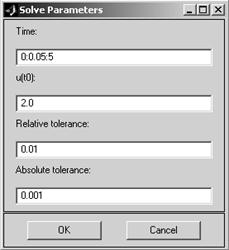начальное условие. Это делается в окне Solve Parameters, которое показано на рис.6. В нём в строке Time надо указать временной диапазон и шаг по нему, а в строке u(t0) – начальное условие. В этом же окне пользователь имеет возможность установить допустимый уровень относительной (Relative tolerance) и абсолютной (Absolute tolerance) погрешности решения задачи Коши.

Для установки необходимой формы представления результатов расчёта, отличной от той, которая задана по умолчанию, следует воспользоваться пунктом меню Plot. Если есть необходимость увидеть процесс видоизменения решения задачи во времени, то в окне Plot Solution надо активизировать строки Height(3-D plot), Animation и Show mesh. В этом случае в графическом окне можно получить мультипликацию трёхмерного изображения решения u (x, y, t), некоторые кадры которой для разных моментов времени показаны на рис.7.

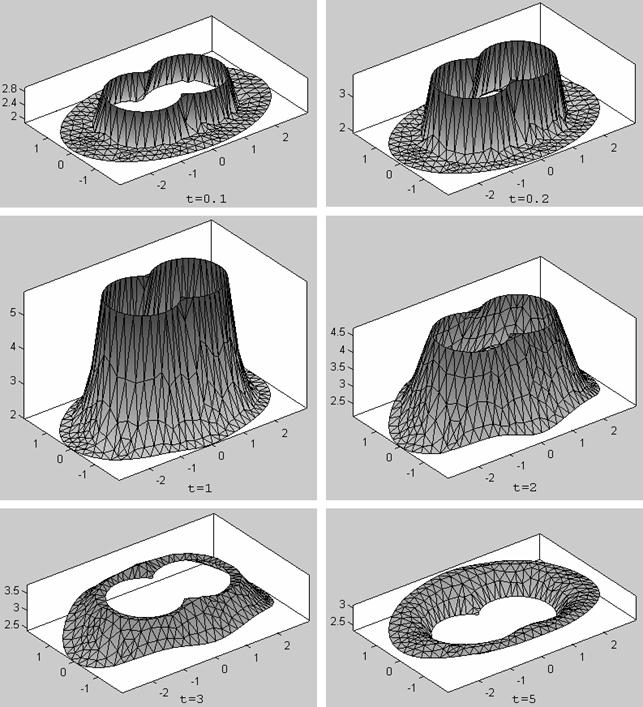
Рис.7.

Контрольные задания

Методом конечных элементов получить решение начально-краевой задачи для параболического уравнения. Область поиска решения указана в соответствии с номером варианта на рис.8–17. Оценить погрешность получаемого решения.

Варианты 1–3 (рис.8).
1.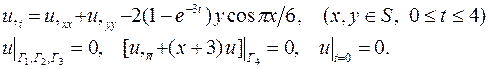
2.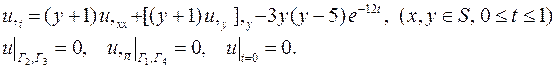
3.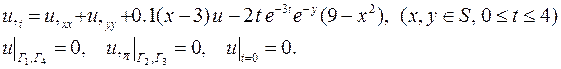
Варианты 4–6 (рис.9).
4.
5.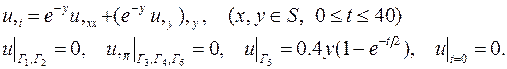
6.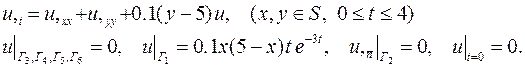
Варианты 7–9 (рис.10).
7.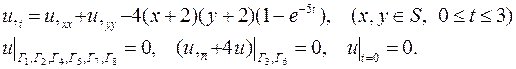
8.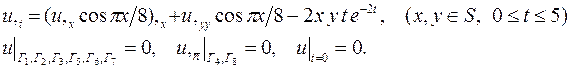
9.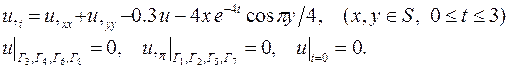
Варианты 10–12 (рис.11).
10.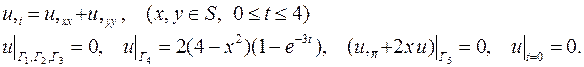
11.
12.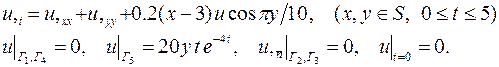

Варианты 13–15 (рис.12).
13.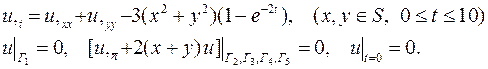
14.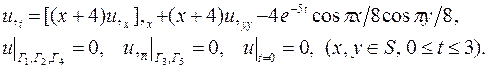
15.
Варианты 16–18 (рис.13).
16.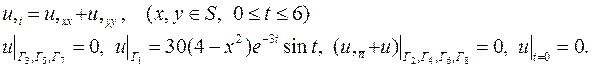
17.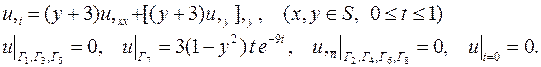
18.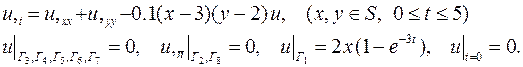
Варианты 19–21 (рис.14).
19.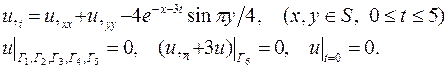
20.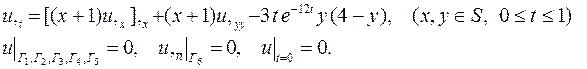
21.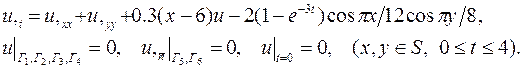
Варианты 22–24 (рис.15).
22.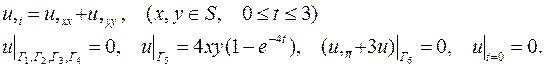
23.
24.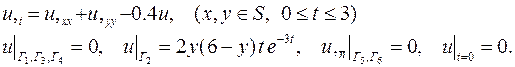

Варианты 25–27 (рис.16).
25.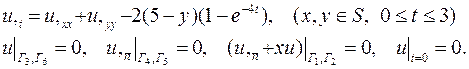
26.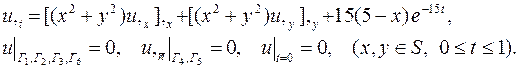
27.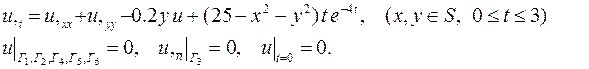
Варианты 28–30 (рис.17).
28.
29.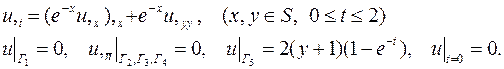
30.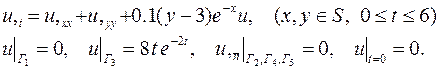

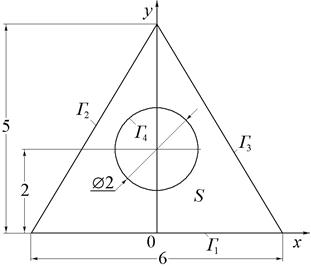
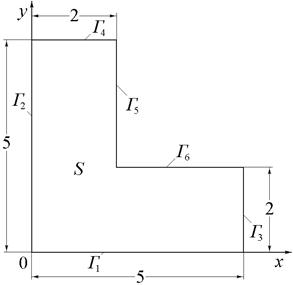
Рис.8 (варианты 1–3).	Рис.9 (варианты 4–6).
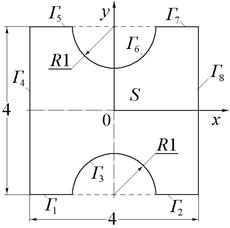
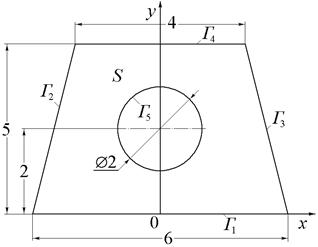
Рис.10 (варианты 7–9).	Рис.11 (варианты 10–12).
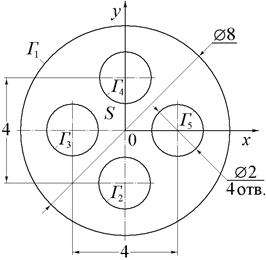
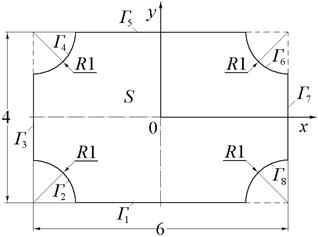
Рис.12 (варианты 13–15).	Рис.13 (варианты 16–18).
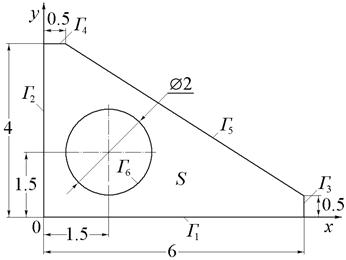
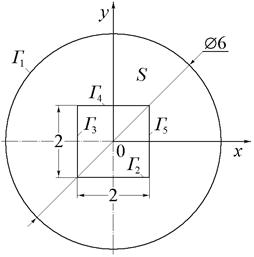
Рис.14 (варианты 19–21).	Рис.15 (варианты 22–24).

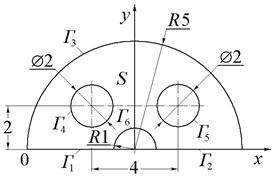
Рис.16 (варианты 25–27).	Рис.17 (варианты 28–30).

Дата добавления: 2014-12-16