Пример решения на ПЭВМ

Программное обеспечение

Для поиска минимума функции нескольких переменных с ограничениями в библиотеке Matlab’а имеется функция fmincon. Обращение к ней осуществляется командой

[x,f]=fmincon(fc,x0,A,b,Aeq,beq,lb,ub,gn,opt,P1,P2,...)

В качестве параметров в этой функции используются:

fc	–	функция в которой вычисляется значения f (x) целевой функции;
x0	–	начальная точка x0 поиска минимума;
A, b	–	параметры линейных ограничений на значения вектора x переменных целевой функции, которые должны быть записаны в стандартизованном виде Ax ≤ b;
Aeq, beq	–	параметры линейных равенств, ограничивающих значения вектора x, которые тоже записываются в стандартизованном виде Aeqx = beq;
lb, ub	–	два вектора, определяющих набор нижних и верхних ограничений на значения вектора x переменных целевой функции: l b ≤ x ≤ u b;
gn	–	функция, задающая левые части нелинейных ограничений. Её стандартизованный вид записывается с помощью равенств p(x)=0 или неравенств q(x) ≤ 0;
opt	–	необязательный параметр, содержащий настройки функции fmincon;
P1,P2,...	–	необязательные параметры, которые могут потребоваться для описания целевой функции или нелинейных ограничений.

Функция fc, вычисляющая значения целевой функции f (x), должна быть оформлена следующим образом:

function f=fc(x,P1,P2,...)

f=......................;

end

Здесь f – переменная, в которой сохраняется значение целевой функции f (x), x – массив значений переменных целевой функции.

Функция gn, описывающая левые части нелинейных ограничений, оформляется в виде:

function [g,p]=gn(x,P1,P2,...)

g(1)=......................;

...........................;

g(k)=......................;

p(1)=......................;

...........................;

p(m)=......................;

end

Здесь g – массив значений вектора g (x) левых частей ограничивающих неравенств, а p – массив значений вектора p (x) левых частей ограничивающих равенств. В случае отсутствия неравенств или равенств в функции gn указываются пустые матрицы

g=[ ] или p=[ ]

В случае отсутствия линейных ограничений

Ax ≤ b, A _eq x = b _eq, l _b ≤ x ≤ u _b

на решение задачи поиска минимума целевой функции при обращении к функции fmincon вместо их параметров тоже устанавливаются пустые матрицы [ ].

Структура opt содержит информацию о настройках функции fmincon. Их перечень можно получить с помощью команды optimset без параметров.

Результатом обращенияк функции fmincon является массив значений x, при которых достигается минимум целевой функции и её значение f.

Условия задачи. Найти абсолютные минимум и максимум функции

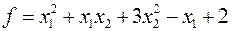
при наличии следующих ограничений

.

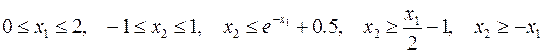Решение. Успешное решение экстремальных задач требует от исследователя последовательного обоснования величин всех используемых в поиске управляющих величин, включая начальную точку поиска.

На первом этапе необходимо выбрать положение начальной точки поиска для чего потребуется построить изображения линий уровня целевой функции с отображением ограничений на её аргументы.

Построение такого контурного графика потребует аккуратного выбора величины конечного штрафа, который будет накладываться на функцию за нарушение установленных ограничений. Величина штрафа должна быть гарантировано больше возможных значений функции на небольшую величину. Для решения этой задачи потребуется построить график исследуемой функции на области, заданной прямыми ограничениями на её аргументы.

x1=linspace(0,2,30); x2=linspace(-1,1,30);

[m1,m2]=meshgrid(x1,x2);

for i=1:30;

for j=1:30;

x=[x1(i) x2(j)]; f(j,i)=fc(x);

end;

end;

surfc(m1,m2,f); colorbar;

xlabel('x1'); ylabel('x2'); zlabel('f');

В программе используется функция fc(x), вычисляющая значения целевой функции:

function f=fc(x)

f=x(1)^2+x(1)*x(2)+3*x(2)^2-x(1)+2;

end

В результате выполнения программы будет выведен график функции, представленный на рис.5.

Рис.5.

Из самого рисунка и цветовой шкалы, приведённой справа, видно, что приблизительный (ряд ограничений не учитывался) диапазон изменения значений функции от 1.5 до 9. Следовательно, значение штрафа можно взять равным 10.

Теперь можно построить контурный график линий уровня целевой функции, используя программу приведённую ниже.

xm1=linspace(0,2,100);

xm2=linspace(-1,1,100);

[mx1,mx2]=meshgrid(xm1,xm2);

for i=1:100;

for j=1:100;

x=[xm1(i) xm2(j)];

[g,p]=gn(x);

if(g(1)<=0 & g(2)<=0 & g(3)<=0);

f(j,i)=fc(x);

else;

f(j,i)=10;

end;

end;

end;

contourf(mx1,mx2,f,20); colorbar;

xlabel('x1'); ylabel('x2');

Данная программа работает совместно с функцией gn, описывающей левые части нелинейных ограничений на область поиска решения. Для написания текста функции сначала надо привести заданные нелинейные ограничения к стандартизованному виду:

,

,

.

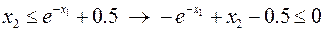Текст функции gn приведён ниже:

function [g,p]=gn(x)

g(1)=-exp(-x(1))+x(2)-0.5;

g(2)=x(1)/2-x(2)-1;

g(3)=-x(1)-x(2);

p=[ ];

end

В результате работы программы будет получено изображение, приведённое на рис.6.

Рис.6.

Полученное изображение используется для определения координат начальной точки поиска. Оно позволяет определить следующие координаты начальной точки (0.5, 0.0).

Для поиска минимума функции остается обратиться к функции fmincon. Это обращение можно задать как в командном окне, так и оформить его в виде отдельного файла

[x,f]=fmincon(@fc,[0.5 0.0],[ ],[ ],[ ],[ ],...

[0 -1],[2 1],@gn)

Результаты работы программы fmincon представлены в виде координат минимума целевой функции и соответствующего им её минимального значения, которые отображаются в командном окне:

x =

0.5455 -0.0909

f =

1.7273

При поиске максимума целевой функции, вследствие того, что функция fmincon ориентирована на поиск минимума, у рассматриваемой целевой функции должен быть изменён знак на обратный. Это делается в функции fc:

f=-(x(1)^2+x(1)*x(2)+3*x(2)^2-x(1)+2);

а в обращении к функции fmincon должны быть заменены координаты начальной точки поиска, которые определяются аналогично координатам начальной точки поиска минимума:

[x,f]=fmincon(@fc,[2.0 0.6],[ ],[ ],[ ],[ ],...

[0 -1],[2 1],@gn)

В этом случае в командном окне получаются следующие координаты и соответствующее значение целевой функции

x =

2.0000 0.6353

f =

-6.4816

Здесь надо помнить, что программа fmincon нашла минимум подправленной целевой функции. Поэтому x ₁ = 2.0000 и x ₂ = 0.6353 являются также координатами точки максимума, где заданная в примере целевая функция принимает значение f = 6.4816.

Контрольные задания

Найти абсолютные минимум и максимум функции при наличии ограничений.

1. ,

.

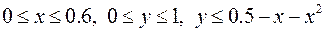2. .

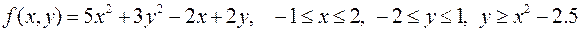3. ,

.

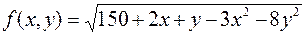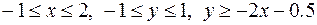4. ,

.

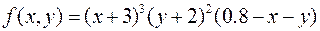5. .

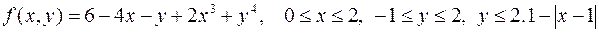6. ,

.

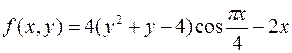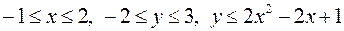7. ,

.

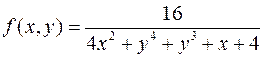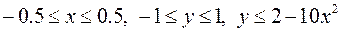8. ,

.

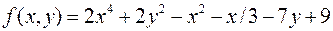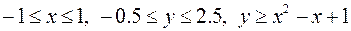9. ,

.

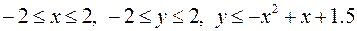10. ,

.

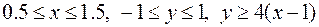11. .

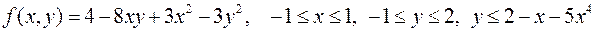12. ,

.

13. ,

.

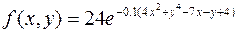14. ,

.

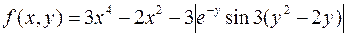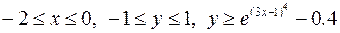15. ,

.

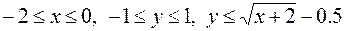16. .

17. ,

.

18. ,

.

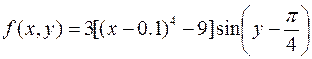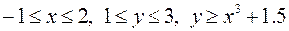19. ,

.

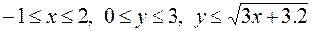20. ,

.

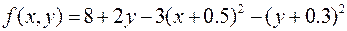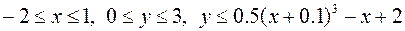21. ,

.

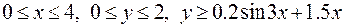22. .

23. ,

.

24. ,

.

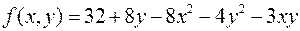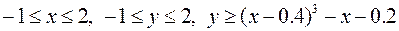25. .

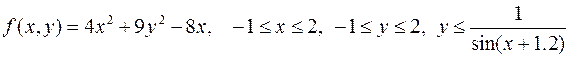26. ,

.

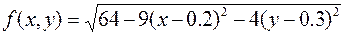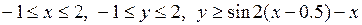27. ,

.

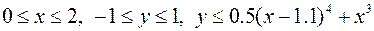28. ,

.

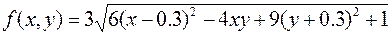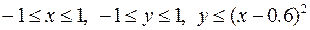29. ,

.

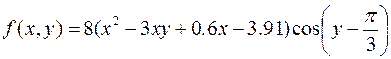30. ,

.

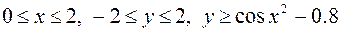СПИСОК ЛИТЕРАТУРЫ

1. Ануфриев И.Е., Смирнов А.Б., Смирнова Е.Н. MATLAB 7. СПб.: БХВ-Петербург, 2005. 1104 с.

2. Бахвалов Н.С., Жидков Н.П., Кобельков Г.М. Численные методы. 3-е изд., перераб. и доп. М.: БИНОМ. Лаборатория знаний, 2003. 632 с.

3. Блохина В.Ф., Лопаницын Е.А., Фролов А.Б. Численные методы. Расчеты в среде MATLAB элементов автомобильных конструкций. М.: Московский государственный машиностроительный университет (МАМИ), 2013. 148 с.

4. Воеводин В.А. Вычислительные основы линейной алгебры. М.: Наука, 1977. 303 с.

5. Волков Е.А. Численные методы. М.: Наука, 1982. 254 с.

6. Зенкевич О. Метод конечных элементов в технике. М.: Мир, 1977. 544 с.

7. Инженерные расчеты на ЭВМ: Справочное пособие. Под ред. В.А.Троицкого. Л.: Машиностроение, 1979. 288 с.

8. Киреев В.И., Пантелеев А.В. Численные методы в примерах и задачах. М.: Высшая школа, 2004. 480 с.

9. Метьюз Д., Финк К. Численные методы. Использование MATLAB. М.- СПб.- К.: «Вильямс», 2001. 716 с.

10. Потемкин В.Г. Введение в Matlab. http://matlab.exponenta.ru/ml /book1.

Варвара Фёдоровна Блохина

Евгений Анатольевич Лопаницын

Александр Борисович Фролов

Численные методы II. Расчеты в среде MATLAB элементов автомобильных конструкций. Учебное пособие по дисциплинам «Методы приближенных вычислений», «Прикладная математика», «Численные методы» для студентов, обучающихся по специальности «Наземные транспортно-технологические средства» и направлениям «Энергетическое машиностроение», «Машиностроение», «Прикладная механика», «Конструкторско-технологическое обеспечение машиностроительных производств» и «Автоматизация технологических процессов и производств».

Подписано в печать Заказ

Формат Печ.л. Уч.-изд.л. Тираж 200

МАМИ Москва 105839 Б.Семёновская, 38.

Дата добавления: 2014-12-16