Пример решения на ПЭВМ. Программное обеспечение

Программное обеспечение

В математической библиотеке Matlab’а для решения краевых задач, записанных для эллиптического уравнения, имеется среда PDE Tool. Её запуск осуществляется с помощью команды

>>pdetool

из командного окна MatLab’а. В результате на экране монитора появляется окно PDE Toolbox’а, которое показано на рис.5.

Рис.5.

Окно PDE Toolbox’а содержит следующие основные элементы:

- меню с перечнем основных операций, необходимых для решения задач;

- панель инструментов рисования геометрических примитивов, определяющих область поиска решения;

- панель инструментов для задания граничных условий, коэффициентов уравнения, построения конечно-элементной сетки, непосредственного решения задачи и визуализации полученных результатов;

- область ввода Set formula для конструирования области из геометрических примитивов;

- поле для построения области поиска решения с осями координат.

Настройка среды PDE Tool и процесс построения с её помощью решения краевой задачи для эллиптического уравнения показаны ниже на примере решения конкретной краевой задачи.

Условия задачи. Найти решение краевой задачи для эллиптического уравнения

,

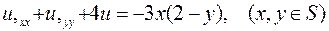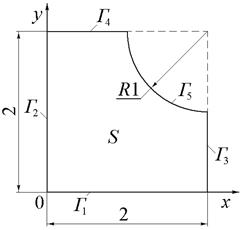
где область S поиска решения показана на рис.6. На границе Г области S заданы следующие граничные условия

,

.

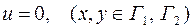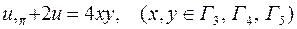Оценить погрешность решения.

Решение. Настройка среды PDE Tool начинается с сохранения проекта: File–Save as–Lr_11.m. Далее из меню PDE Toolbox’а с помощью цепочки команд Options–Application–Generic Scalar устанавливается режим решения краевой задачи для одного эллиптического уравнения. После этого решение задачи строится в 6 этапов.

1. Создание системы глобальных координат. Из меню PDE Toolbox’а по цепочке команд Options–Axis Limit задаются размеры отображаемой части пространства { x, y } в виде X-axis range: [0 3] и Y-axis range: [0 3]. После этого устанавливается одинаковый масштаб по обеим осям: Options–Axis Equal и отображение координатной сетки: Options–Grid. Результат этих действий показан на рис.7.

2. Формирование области S поиска решения. Для этого по цепочке команд Draw–Rectangle/Square надо перейти в режим рисования прямоугольника (альтернатива – кнопка панели инструментов) и, устанавливая курсор в нужные точки экрана, координаты которых отображаются в правом верхнем окне построения области, нарисовать квадрат со стороной в 2 единицы. Он будет обозначен R1. Затем по цепочке команд Draw–Ellipse/Circle (centered) (альтернатива – кнопка панели инструментов) из верхнего правого угла квадрата надо нарисовать окружность с радиусом 1 который будет обозначен E1. Теперь надо удалить круг из квадрата. Для этого в окне Set formula следует набрать «R1-E1» и перейти к заданию типа решаемого уравнения по цепочке команд: PDE–PDE Mode. Результат этого показан на рис.8.

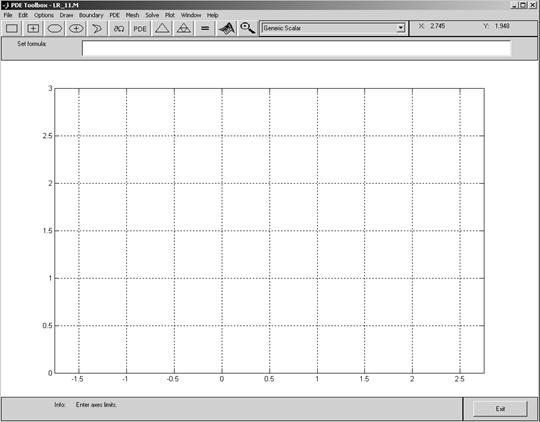
Рис.7.

Рис.8.

3. Выбор типа уравнения и задание его коэффициентов. Сначала надо привести заданное эллиптическое уравнение к используемой в PDE Tool форме:

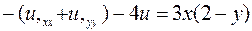
или

.

После этого по цепочке команд PDE–PDE Specification (альтернатива – кнопка панели инструментов) следует задать уравнение – elliptic, а коэффициенты c, a и f следующими числами и выражением: 1, -4 и 3*x.*(2-y), как показано на рис.9.

Рис.9.

4. Задание граничных условий. Здесь тоже сначала надо привести заданное граничное условие 2-го типа к используемой в PDE Tool форме:

.

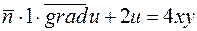Затем по цепочке команд Boundary–Show Edge Labels и Boundary–Mode следует выставить нумерацию участков границы области поиска решения 1, 2, 3, 4 и 5, иеаryчное условие 2-го типа ем: 1, -4 и 3*чю* используемому виду в войти в режим задания граничных условий на каждом участке границы. Этот режим предполагает активизацию левой клавишей «мыши» указанного курсором участка границы и по цепочке команд Boundary–Specify Boundary Conditions задание типа граничного условия и его коэффициентов (см. рис.10). Допускается активизация сразу нескольких участков границ при нажатой клавише Shift. Для задания на участках 1 и 2 граничного условия 1-го типа надо выбрать пункт Dirichlet и задать h и r равными 1 и 0, а для задания на участках 3, 4, 5 и 6 граничного условия 2-го типа надо выбрать пункт Neumann и задать g и q равными 4*x.*y и 2. После выполнения этого пункта алгоритма решения на экране монитора будет изображение, показанное на рис.11.

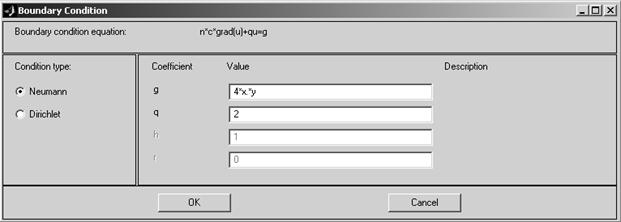
Рис.10.

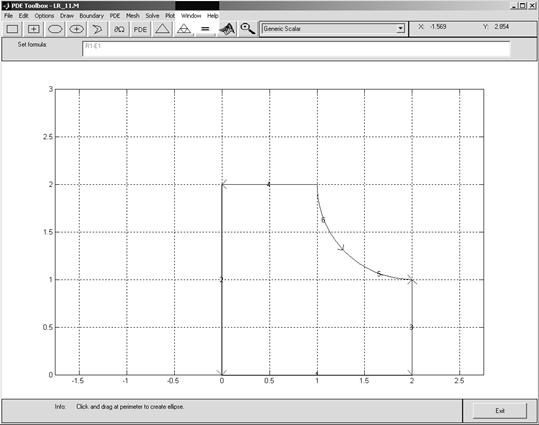
Рис.11.

5. Формирование конечно-элементной сетки. Этот этап осуществляется цепочкой команд Mesh–Initialize Mesh (альтернатива – кнопка панели инструментов). Получающаяся при этом сетка показана на рис.12. Если необходима в два раза более густая сетка, то её можно сформировать командой Mesh–Refine Mesh (альтернатива – кнопка панели инструментов).

Рис.12.

6. Построение конечно-элементного решения осуществляется цепочкой команд Solve–Solve PDE. Результатом её выполнения будет цветная диаграмма, показанная на рис.13. По ней с помощью расположенной слева в окне палитры можно получить представлении о виде и величине решения u (x, y) рассматриваемой краевой задачи.

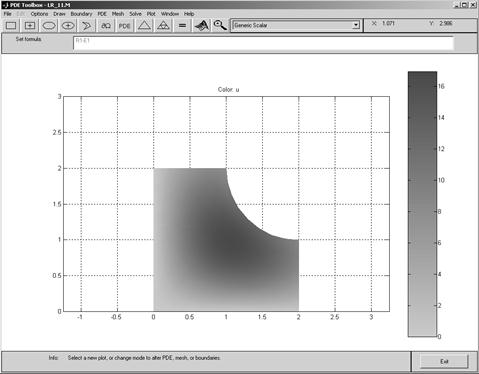
Рис.13.

В случае, когда форма представления решения не удовлетворяет каким-либо требованиям, её можно изменить. Для этого по цепочке команд Plot–Plot Solution можно попасть в меню установок визуализации решения (см. рис.14), предоставляющее пользователю широкие возможности (альтернатива – кнопка панели инструментов). Например, если кроме пункта Color активизировать ещё пункты Height(3-D plot) и Show mesh, то в графическом окне Matlab’а получится трёхмерное изображение решения, показанное на рис.15.

Рис.14.

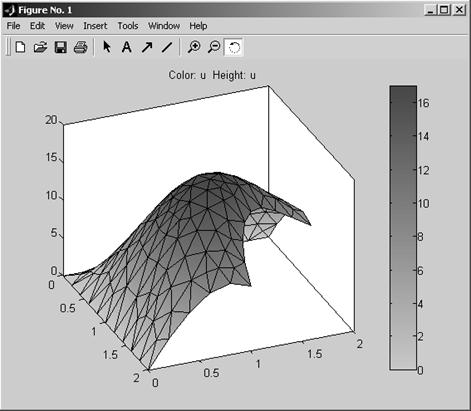
Рис.15.

Для оценки погрешности полученного решения следует воспользоваться правилом Рунге. Для этого часто достаточно снять с трёхмерного изображения, которое можно поворачивать, только наибольшее значение решения u (x, y). В данном случае оно будет равно 16.8. После этого надо повторить расчёт с более густой (в 2 раза) сеткой и опять получить наибольшее значение решения u _max = 17.2. По итогам этих замеров можно оценить погрешность более точного решения по правилу Рунге

.

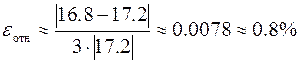По окончании работы с PDE Tool следует сохранить полученные результаты в своём наборе данных, маршрут на который должен был ранее установлен при открытии Matlab’а. Это можно сделать с помощью цепочки команд File–Save as. После этого, при необходимости, конечно-элементная модель краевой задачи может быть загружена в PDE Tool цепочкой команд File–Open.

Контрольные задания

Методом конечных элементов получить решение краевой задачи для эллиптического уравнения. Область поиска решения указана в соответствии с номером варианта на рис.16–25. Дать оценку погрешности получаемого решения.

Варианты 1–3 (рис.16).
1.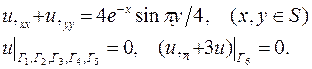
2.
3.

Варианты 4–6 (рис.17).
4.
5.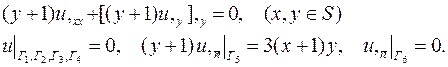
6.
Варианты 7–9 (рис.18).
7.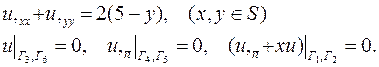
8.
9.
Варианты 10–12 (рис.19).
10.
11.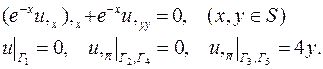
12.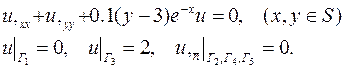
Варианты 13–15 (рис.20).
13.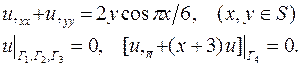
14.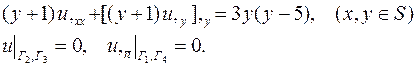
15.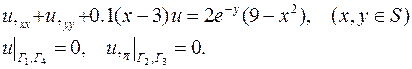

Варианты 16–17 (рис.21).
16.
17.
18.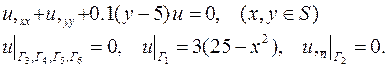
Варианты 19–21 (рис.22).
19.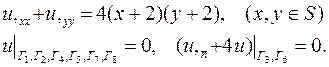
20.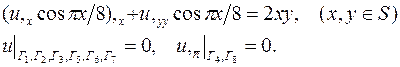
21.
Варианты 22–24 (рис.23).
22.
23.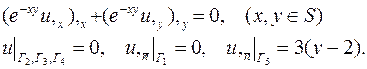
24.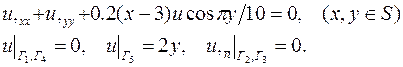
Варианты 25–27 (рис.24).
25.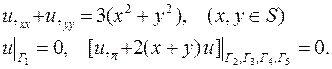
26.
27.

Варианты 28–30 (рис.25).
28.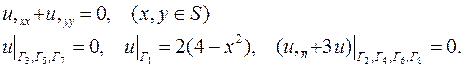
29.
30.

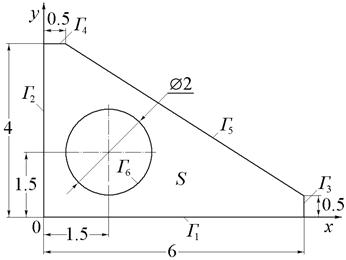
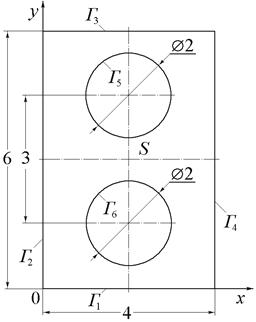
Рис.16 (варианты 1–3).	Рис.17 (варианты 4–6).

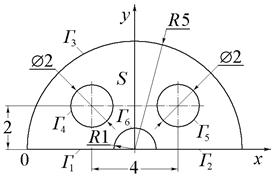
Рис.18 (варианты 7–9).	Рис.19 (варианты 10–12).

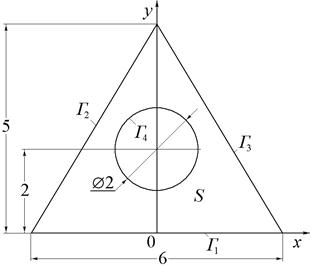
Рис.20 (варианты 13–15).	Рис.21 (варианты 16–18).
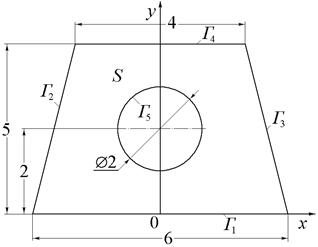
Рис.22 (варианты 19–21).	Рис.23 (варианты 22–24).
Рис.24 (варианты 25–27).	Рис.25 (варианты 28–30).

Дата добавления: 2014-12-16