Вариационная постановка краевой задачи

Вариационная постановка краевой задачи для эллиптического уравнения состоит в формировании функционала, чья экстремаль совпадает с решением данной задачи. В частности, можно показать, что из условия экстремума функционала

,

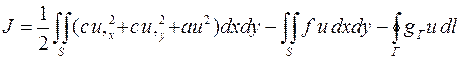где функции f = f (x, y) и g_Г = g_Г (x, y) считаются известными и поэтому не подлежат варьированию, следует эллиптическое уравнение для области S и упомянутые ранее граничные условия для контура Г.

На самом деле, вариация функционала будет иметь вид

.

Если в первом интеграле к первым двум слагаемым применить интегрирование «по частям» и принять

,

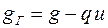то вариацию функционала можно записать

.

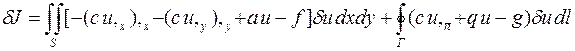Отсюда, применяя необходимое условие существования экстремума функционала

,

можно получить эллиптическое уравнение

и возможные варианты граничных условий

.

Первое граничное условие совпадает с граничным условием, которое ставится для задачи Неймана, а второе – приводится к граничному условию задачи Дирихле

.

Дискретизация области поиска решения

По своей сути метод конечных элементов является методом дискретизации рассматриваемой задачи, когда её приближённое решение ищется в виде непрерывной функции, значения которой определяются конечным числом узловых значений. В результате использования такого подхода краевая задача для уравнения с частными производными приводится к системе алгебраических уравнений относительно узловых значений искомой функции.

При таком подходе область S поиска решения задачи делится на подобласти – конечные элементы, как это показано на рис.2, где использованы треугольные конечные элементы. В простейшем случае считается, что конечные элементы связаны друг с другом только в своих вершинах.

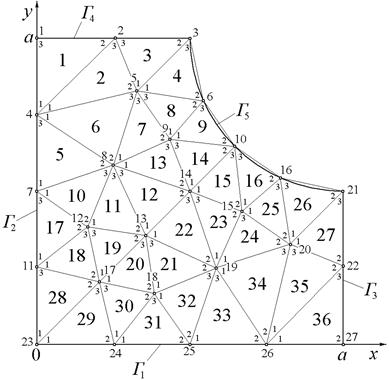
Рис.2.

На рис.2 область поиска решения разбита на N _эл = 36 треугольных элементов, которые соединены N _уз = 27 узлами. Каждый узел конеч-но-элементной сетки и каждый её элемент имеют свой неповторяющийся номер, при этом внутри каждого элемента используют внутреннюю, локальную нумерацию узлов, выполняемую против часовой стрелки.

Результатом дискретизации области поиска решения являются две таблицы. Первая из них содержит перечень номеров узлов конечно-элементной сетки с их координатами и значениями переменных коэффициентов эллиптического уравнения и его граничных условий. Её содержимое для области S в виде квадрата со стороной a = 2 и одним углом, вырезанным по окружности радиусом R = 1 (см. рис.2), а также для f (x, y) = –3 x (2 – y), a (x, y) = 4, с (x, y) = 1, q (x, y) = 2, g (x, y) = 4 xy, h (x, y) = 1 и r (x, y) = 0 показан в таблице 1.

Вторая таблица служит для связи локальной нумерации узлов в каждом элементе с их глобальной нумерацией в области S и для задания граничных условий на сторонах конечных элементов, которые являются граничными. Она имеет вид таблицы 2. В этой таблице каждой стороне каждого элемента поставлено численное значение признака постановки граничного условия. Его значение 0 означает, что

Таблица 1.

Но-мер узла	Абс-цисса x узла	Орди- ната y узла	с (x, y)	a (x, y)	f (x, y)	q (x, y)	g (x, y)	h (x, y)	r (x, y)
	0.5
		1.5
	0.653	1.66			–0.666		4.34
…	…	…	…	…	…	…	…	…	…
	1.5				–9
					–12

Таблица 2.

Но- мер эле- мен- та	Глоба- льный номер 1-го узла эле- мента	Глоба- льный номер 2-го узла эле- мента	Глоба- льный номер 3-го узла эле- мента	Признак постановки граничного условия на стороне элемента
Сто- рона 1 – 2	Сто- рона 2 – 3	Сто- рона 3 – 1
…	…	…	…	…	…	…

эта сторона элемента – внутренняя для области S. В противном случае, когда сторона элемента является частью границы Г, признак постановки граничных условий принимает значения 1 или 2. Это означает, что на этой стороне элемента ставится граничное условие первого (задача Дирихле) или второго (задача Неймана) типов, соответственно.

Аппроксимация решения в треугольном элементе

Система координат x 0 y, в которой рассматривается область S поиска решения, в методе конечных элементов традиционно принято называть глобальной. При этом каждый элемент конечно-элементной сетки, как показано на рис.3, принято описывать в своей, локальной системе координат ξ 0 η.

Рис.3.

Всем локальным номерам (1, 2 и 3) узлов соответствуют глобальные номера: i_n, j_n и k_n. При этом центр локальной системы координат помещается в 1-й узел, а её абсцисса ξ направляется от 1-го узла ко 2-му.

Решение исходной краевой задачи в пределах каждого элемента представляется приближённо какой-либо известной функцией, которая описывается через свои узловые значения. Количество этих узловых значений в каждом узле называется числом степеней свободы каждого узла, а их общее количество для всего элемента – числом степеней свободы элемента.

Постановка рассматриваемой краевой задачи допускает применение узлов с 1-й степенью свободы. Поэтому для трёхузлового элемента искомое решение u (x, y) в пределах каждого элемента может быть представлено функцией с тремя параметрами. В простейшем случае это – билинейная функция

,

которая записывается в матричной форме:

,

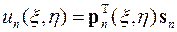где

, .

Коэффициенты представления искомой функции u_n описываются через её значения в узлах элемента

узел 1: ,

узел 2: ,

узел 3: .

Это – система линейных алгебраических уравнений. В матричной форме она имеет вид

,

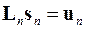где

, .

Имея связь s _n и u _n можно осуществить обратный переход

,

В итоге искомая функция в пределах треугольного элемента будет

.

При этом вектор u _n называется вектором обобщённых значений искомой функции конечного элемента.

Аналогично в пределах каждого элемента описываются переменные коэффициенты эллиптического уравнения и его граничных условий

,

,

где в отличие от вектора u _n векторы с _n, a _n, f _n, q _n, g _n, h _n и r _n известны, поскольку их компоненты берутся из таблиц 1 и 2

,

,

.

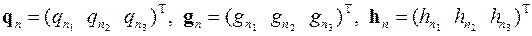Функционал треугольного элемента

Наличие описания решения u (x, y) в пределах конечного элемента позволяет записать для него функционал, эквивалентный рассматриваемой краевой задачи. Принимая во внимание инвариантность функционала по отношению к повороту и переносу координатных осей его можно представить в локальной системе координат в виде

.

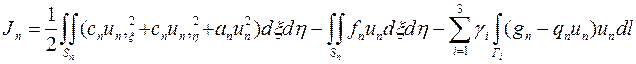Здесь интеграл по контуру элемента представлен суммой интегралов по каждой его стороне, коэффициенты γ ₁, γ ₂, и γ ₃ принимают значение 1, если рассматриваемая сторона элемента является частью границы Г области S и на ней задано граничное условие 2-го типа, и значение 0 в противном случае, а частные производные решения описываются следующими соотношениями

,

где

.

Подстановка представления искомого решения и переменных коэффициентов эллиптического уравнения и его граничных условий в функционал позволяет записать его в виде

.

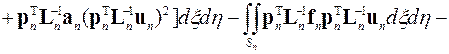
Это выражение для функционала можно преобразовать, вынеся из-под интегралов сомножители, не зависящие от координат ξ и η

.

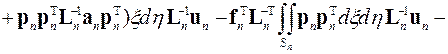
Обозначение интегралов в функционале следующим образом

,

,

,

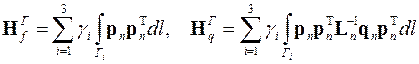позволяет привести его выражение к виду

и рассмотреть структуру подынтегральных выражений. Все эти интегралы будут квадратными симметричными матрицами

,

,

.

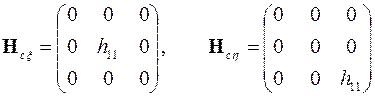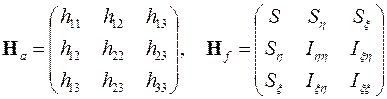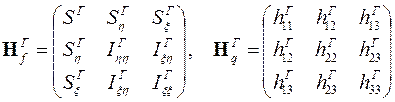Их элементы вычисляются с помощью площади конечного элемента

,

его статических моментов и моментов инерции

,

,

его моментов 3-го порядка

,

,

а также подобных им интегралов по контуру конечного элемента

,

,

,

.

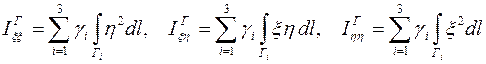Приведённые интегралы допускают аналитическое представление посредством приёмов, известных из интегрального исчисления.

Окончательную форму записи функционала конечного элемента обычно принимают в виде

,

где K _n – квадратная симметричная матрица (3×3 элем.), которую традиционно принято называть матрицей жёсткости элемента, B _n – тоже квадратная симметричная матрица (3×3 элем.) жёсткости границы элемента, а z _n и b _n – векторы внешнего воздействия (по 3 элем.) на конечный элемент

,

.

Функционал для всей области поиска решения

Функционал для всей области S поиска решения рассматриваемой краевой задачи будет равна сумме функционалов всех её элементов

.

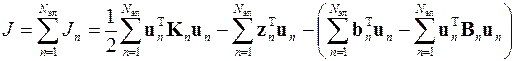Эти суммы можно представить в матричной форме

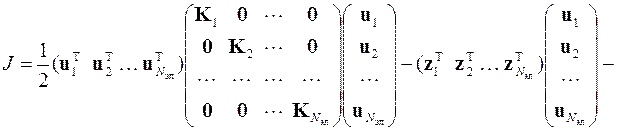
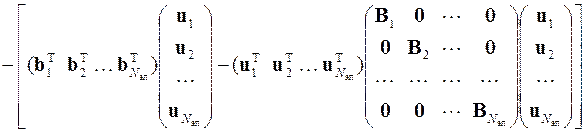
или

,

где K ₀ и B ₀ – объединённые блочные матрицы жёсткости области S поиска решения и её границы Г, z ₀ и b ₀ – объединённые векторы внешнего воздействия на них, а u ₀ – объединённый вектор решения в узлах конечных элементов

,

.

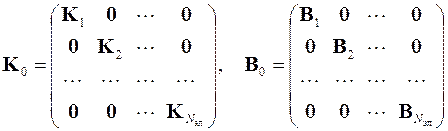Порядок объединённых матриц жёсткости определяется произведением N _эл ´ 3 узла ´ 1 степ. своб. в узле. Такой же порядок имеют объединённые векторы решения и внешнего воздействия, которые тоже является блочными векторами.

Полученная форма представления функционала задачи не учитывает способа соединения элементов в область поиска решения заданной конфигурации. Поэтому надо записать компоненты объединённого вектора решения в узлах конечных элементов через вектор обобщённого решения в узлах всей области S

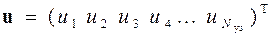
Для этого следует рассмотреть, по крайней мере, 1-й элемент области (см. рис.2 и 4).

Рис.4.

Значения решения в узлах этого элемента имеют обозначения . В то же время эти значения являются значениями решения в узлах всей конечно-элементной сетки, которые обозначены как . В связи с этим можно записать равенства

, , ,

которые в матричной форме дают

.

Таким же способом можно описать связь локальных значений решения других конечных элементов с узловыми значениями обобщённого решения для всей области S в глобальной системе координат. В результате получается связь всех блоков объединённого вектора решений в узлах элементов с вектором обобщённого решения в узлах рассматриваемой области S

,

где Г – матрица геометрии составлена из блоков по три строки, один из которых показан на примере вектора u ₁.

Размерность вектора обобщённого решения меньше, чем размерность объединённого вектора. Она вычисляется как N _уз ´ 1 степ. своб. в узле. Матрица Г геометрии пространственного тела – прямоугольная матрица размером (N _эл ´ 3 узла ´ 1 степ. своб. в узле) строк на (N _уз ´ 1 степ. своб. в узле) столбцов. Её ненулевые компоненты формируются для каждого элемента области S в соответствии с первыми четырьмя колонками таблицы 2.

В итоге функционал краевой задачи для всей области S поиска решения будет равен

,

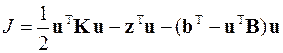где K = Г ^Т K ₀ Г и B = Г ^Т B ₀ Г – матрицы жёсткости области S поиска решения и её границы Г, а z = Г ^Т z ₀ и b = Г ^Т b ₀ – векторы внешнего воздействия на них.

Конечно-элементная форма представления краевой задачи

Для получения конечно-элементных уравнений рассматриваемой краевой задачи необходимо потребовать минимума её функционала в виде необходимого условия его экстремума

.

Подстановка в это вариационное уравнение ранее полученного выражения для функционала и выполнение в нём операции варьирования вектора обобщённого решения позволяет получить следующее выражение

.

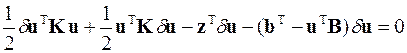Это вариационное уравнение можно упростить, принимая во внимание симметричность матриц K и B

или

.

Сравнение множителей при вариациях компонент обобщённого вектора решения даёт следующее матричное уравнение

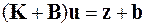
или

,

где

.

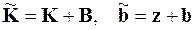Полученное матричное уравнение представляет собой систему линейных алгебраических уравнений относительно значений решений в узлах конечно-элементной сетки – , образующих обобщённый вектор u решения для всей области S

.

Методы решения таких систем известны по разделу «Решение систем линейных алгебраических уравнений» [3]. Однако прежде чем решать полученную систему алгебраических уравнений, её надо преобразовать так, чтобы она учитывала граничные условия 1-го типа, образующие совместно с эллиптическим уравнением краевой задачу Дирихле.

Задание граничных условий в методе конечных элементов

В отличие от классической постановки краевой задачи для эллиптического уравнения, где граничные условия ставятся на контуре Г области S поиска решения, в методе конечных элементов граничные условия ставятся только в узловых точках этого контура. При этом надо помнить, что в методе конечных элементов граничные условия 2-го типа в узловых точках выполняются автоматически в силу его вариационной постановки. Поэтому в контурных точках внешней границы области S надо учитывать только граничные условия 1-го типа, если они в них заданы.

Допустим, что граничные условия 1-го типа заданы на участ­ках Г ₁ и Г ₂ границы Г (см. рис.2)

,

где

.

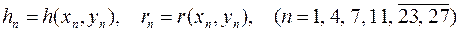Тогда решение полученной выше системы линейных алгебраических уравнений должно давать те же значения для u ₁, u ₄, u ₇,…, u ₂₇, что получаются из этих граничных условий.

Это достигается тем, что вместо диагональных элементов матрицы жёсткости, соответствующих u ₁, u ₄, u ₇,…, u ₂₇, ставятся величины h ₁, h ₄, h ₇,…, h ₂₇ вместе с обнулением остальных элементов их строк и столбцов. При этом соответствующие элементы вектора внешнего воздействия заменяются на величины r ₁, r ₄, r ₇,…, r ₂₇.

.

Оценка погрешности решения

Основными составляющими погрешности приближённых решений краевых задач для эллиптических уравнений, получаемых методом конечных элементов, являются погрешность аппроксимации решения в пределах конечного элемента, погрешность представления области поиска решения конечными элементами и погрешность решения системы линейных алгебраических уравнений. Дать априорную оценку погрешности приближённого решения, получаемого с помощью такого разнопланового вычислительного процесса, затруднительно. Поэтому на практике для вычисления погрешности используют апостериорную оценку, базирующуюся на правиле Рунге.

Если имеется два решения краевой задачи для эллиптического уравнения с размерами конечных элементов, отличающихся в два раза или, что практически то же самое, отличающиеся количеством конечных элементов в четыре раза, то абсолютная погрешность более точного решения может быть оценена соотношением

.

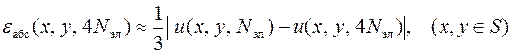В качестве относительной погрешности решения краевой задачи используют её интервальную оценку

.

Такой подход вполне оправдан до тех пор, пока при реализации вычислений не начинают сказываться неустранимые ошибки округления.

Дата добавления: 2014-12-16